冀教版八年级数学下册第二十二章 四边形测试题(Word版 含答案)
文档属性
| 名称 | 冀教版八年级数学下册第二十二章 四边形测试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 316.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 14:22:22 | ||
图片预览



文档简介
第二十二章 四边形
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
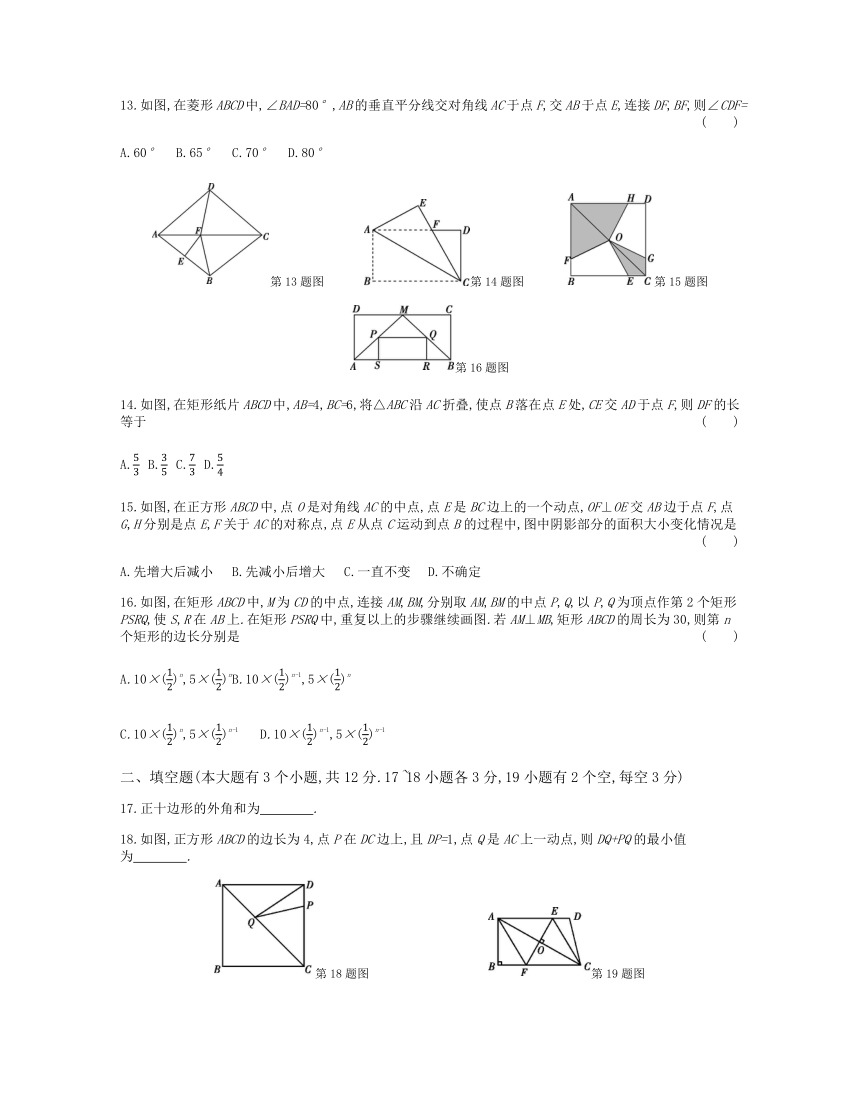
1.下列说法正确的是( )
A.对角线相等且互相垂直的四边形是菱形
B.对角线互相平分的四边形是正方形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等且互相平分的四边形是矩形
2.若一个多边形的内角和是外角和的2倍,则它是( )
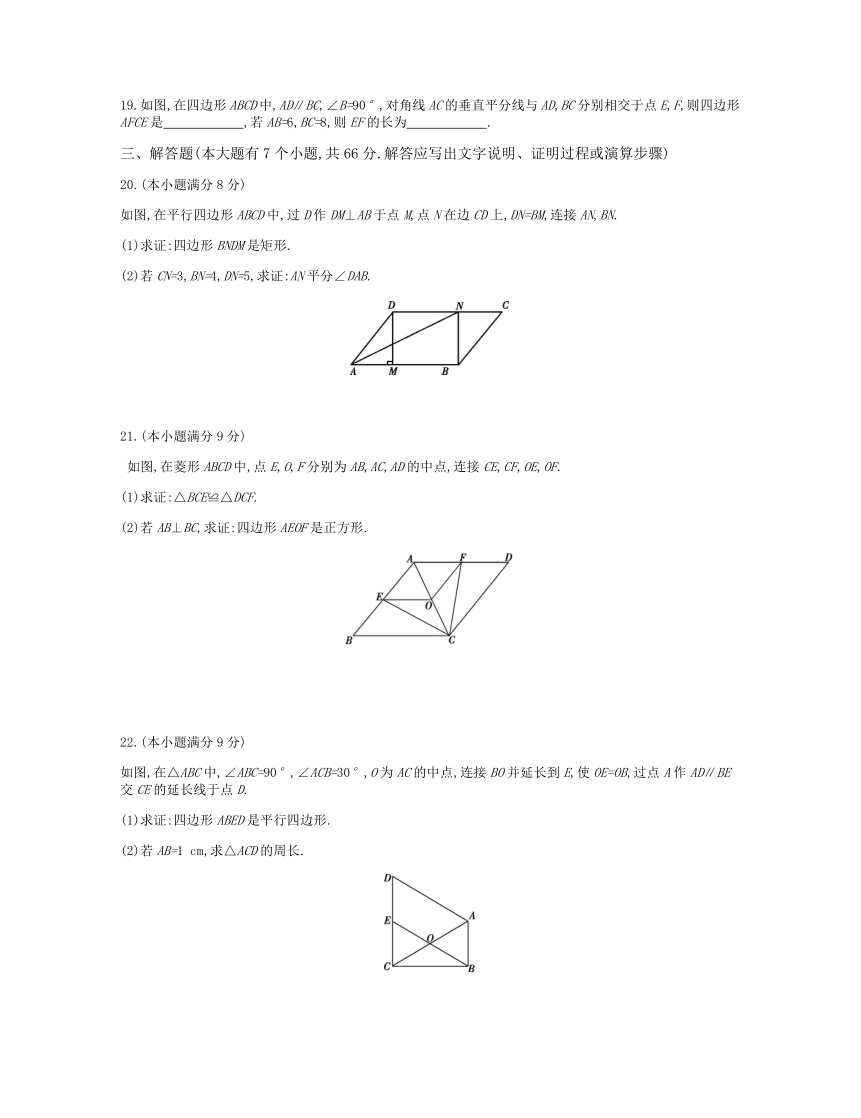
A.四边形 B.五边形 C.六边形 D.八边形
3.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,且BD=16,则EF=( )
A.32 B.16
C.8 D.4
4.要使四边形ABCD是平行四边形,则∠A∶∠B∶∠C∶∠D可能为( )
A.4∶5∶4∶5 B.3∶4∶5∶6 C.3∶3∶5∶5 D.2∶3∶6∶7
5.若一个菱形的周长是20 cm,两条对角线的比是4∶3,则这个菱形的面积是( )
A.12 cm2 B.24 cm2 C.48 cm2 D.96 cm2
6.如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=100°,则∠DAE的度数为( )
A.10° B.20° C.30° D.40°
第6题图 第7题图 第8题图 第9题图
7.已知?ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
A.∠DAE=∠BAE B.∠DEA=12∠DAB
C.DE=BE D.BC=DE
8.如图,?ABCD的对角线AC,BD相交于点O,点E是AB的中点,△BEO的周长为8,则△BCD的周长为( )
A.8 B.10 C.16 D.20
9.如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
A.75° B.60° C.54° D.67.5°
10.如图,四边形ABCD是矩形,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.若AB=2,则△OEC的面积为( )
A.1 B.2 C.3 D.4
第10题图 第11题图 第12题图
11.如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形 B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形 D.若AD平分∠BAC,则四边形AEDF是菱形
12.如图,在平行四边形ABCD中,∠ABC的平分线BF交AD于点F,FE∥AB.若AB=5,BF=6,则四边形ABEF的面积为( )
A.48 B.35 C.30 D.24
13.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,交AB于点E,连接DF,BF,则∠CDF=( )
A.60° B.65° C.70° D.80°
第13题图 第14题图 第15题图 第16题图
14.如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
A.53 B.35 C.73 D.54
15.如图,在正方形ABCD中,点O是对角线AC的中点,点E是BC边上的一个动点,OF⊥OE交AB边于点F,点G,H分别是点E,F关于AC的对称点,点E从点C运动到点B的过程中,图中阴影部分的面积大小变化情况是( )
A.先增大后减小 B.先减小后增大 C.一直不变 D.不确定
16.如图,在矩形ABCD中,M为CD的中点,连接AM,BM,分别取AM,BM的中点P,Q,以P,Q为顶点作第2个矩形PSRQ,使S,R在AB上.在矩形PSRQ中,重复以上的步骤继续画图.若AM⊥MB,矩形ABCD的周长为30,则第n个矩形的边长分别是( )
A.10×(12)n,5×(12)n B.10×(12)n-1,5×(12)n
C.10×(12)n,5×(12)n-1 D.10×(12)n-1,5×(12)n-1
二、填空题(本大题有3个小题,共12分.17~18小题各3分,19小题有2个空,每空3分)
17.正十边形的外角和为 .?
18.如图,正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为 .?
第18题图 第19题图
19.如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与AD,BC分别相交于点E,F,则四边形AFCE是 ,若AB=6,BC=8,则EF的长为 .?
三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)
如图,在平行四边形ABCD中,过D作DM⊥AB于点M,点N在边CD上,DN=BM,连接AN,BN.
(1)求证:四边形BNDM是矩形.
(2)若CN=3,BN=4,DN=5,求证:AN平分∠DAB.
21.(本小题满分9分)
如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF.
(2)若AB⊥BC,求证:四边形AEOF是正方形.
22.(本小题满分9分)
如图,在△ABC中,∠ABC=90°,∠ACB=30°,O为AC的中点,连接BO并延长到E,使OE=OB,过点A作AD∥BE交CE的延长线于点D.
(1)求证:四边形ABED是平行四边形.
(2)若AB=1 cm,求△ACD的周长.
23. (本小题满分9分)
在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC相交于点D,求证:EF=12(AC-AB);
(2)如图2,请直接写出线段AB,AC,EF之间的数量关系.
24.(本小题满分10分)
如图,四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)若AB=2,CE=2,求CG的长度.
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
25.(本小题满分10分)
如图1,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD的中点,连接AB',C'D,AD',BC',AC',如图2.
(1)求证:四边形AB'C'D是菱形.
(2)四边形ABC'D'的周长为 .?
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形的周长.
26. (本小题满分11分)
在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,按顺时针方向旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(1)如图1,当点D落在BC边上时,求点D的坐标.
(2)如图2,当点D落在线段BE上时,AD与BC交于点H.
①求证:△ADB≌△AOB;
②求点H的坐标.
(3)连接OC,AB,记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
D
C
C
A
B
B
C
C
B
A
D
D
A
A
C
D
17.360° 18.5 19.菱形 152
20. (1)∵四边形ABCD为平行四边形,
∴DC∥AB,∴DN∥BM.
∵DN=BM,∴四边形BNDM是平行四边形.
∵DM⊥AB,∴∠DMB=90°,
∴四边形BNDM是矩形.
(2)由(1)得四边形BNDM是矩形,
∴∠DNB=90°,∴∠BNC=90°.
∵CN=3,BN=4,∴BC=5,∴AD=BC=5.
∵DN=5,∴DN=AD,∴∠DAN=∠DNA.
∵DC∥AB,∴∠DNA=∠NAB,∴∠DAN=∠NAB,
∴AN平分∠DAB.
21. (1)∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD.
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF.
在△BCE和△DCF中,BE=DF,∠B=∠D,BC=DC,
∴△BCE≌△DCF(SAS).
(2)由题意得,OF=12DC,OE=12BC,OE∥BC,∴AE=OE=OF=AF,
∴四边形AEOF是菱形.
∵AB⊥BC,OE∥BC,
∴OE⊥AB,∴∠AEO=90°,
∴四边形AEOF是正方形.
22. (1)如图,连接AE.
∵OA=OC,OB=OE,
∴四边形ABCE是平行四边形,∴CD∥AB.
∵AD∥BE,∴四边形ABED是平行四边形.
(2)∵四边形ABCE是平行四边形,∠ABC=90°,
∴四边形ABCE是矩形,
∴∠BCE=90°.
∵∠ACB=30°,∴∠ACD=60°.
∵AB=CE=ED=1,AC=2AB=2,
∴CD=AC=2,∴△ACD是等边三角形,
∴△ACD的周长为6.
23. (1)∵AE⊥BD,∴∠AED=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠DAE+∠ADE=90°.
∵∠BAE=∠DAE,∴∠ABE=∠ADE,∴AB=AD.
∵AE⊥BD,∴BE=DE,
又∵BF=FC,∴EF=12DC=12(AC-AD)=12(AC-AB).
(2)EF=12(AB-AC).
如图,延长AC交BE的延长线于点P,
∵AE⊥BP,∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°.
∵∠BAE=∠PAE,∴∠ABE=∠APE,
∴AB=AP.
∵AE⊥BP,∴BE=PE,
又∵BF=FC,∴EF=12PC=12(AP-AC)=12(AB-AC).
24. (1)如图1,作EP⊥CD于点P,EQ⊥BC于点Q,
∵∠DCA=∠BCA,EC=EC,
∴△EQC≌△EPC,
∴EQ=EP.
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED.
在Rt△EQF和Rt△EPD中,∠QEF=∠PED,EQ=EP,∠EQF=∠EPD,
∴Rt△EQF≌Rt△EPD,∴EF=ED,
∴矩形DEFG是正方形.
(2)如图2,在Rt△ABC中,AC=2AB=2 2,
∵EC=2,∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=2.
(3)∠EFC=120°或∠EFC=30°.
①当DE与AD的夹角为30°时,∠EFC=120°;
②当DE与DC的夹角为30°时,∠EFC=30°.
综上所述,∠EFC=120°或∠EFC=30°.
25. (1)∵BD是矩形ABCD的对角线,∠ABD=30°,
∴∠ADB=60°,
由平移可得,B'C'=BC=AD,∠D'B'C'=∠DBC=∠ADB=60°,
∴AD∥B'C',∴四边形AB'C'D是平行四边形.
∵B'为BD的中点,
∴在Rt△BAD中,AB'=12BD=DB'.
又∵∠ADB=60°,
∴△ADB'是等边三角形,∴AD=AB',
∴四边形AB'C'D是菱形.
(2)43
由平移可得,AB=C'D',∠ABD'=∠C'D'B=30°,
∴AB∥C'D',∴四边形ABC'D'是平行四边形.
由(1)可得,AC'⊥B'D,∴四边形ABC'D'是菱形.
∵AB=3AD=3,
∴四边形ABC'D'的周长为43.
(3)拼成的矩形的周长是6+3或23+3.
将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,如图所示:
∴拼成的矩形的周长为6+3或2 3+3.
26. (1)∵A(5,0),B(0,3),∴OA=5,OB=3.
∵四边形AOBC是矩形,
∴AC=OB=3,OA=BC=5,∠OBC=∠C=90°.
∵矩形ADEF是由矩形AOBC旋转得到的,∴AD=AO=5.
在Rt△ACD中,CD=AD2-AC2=4,
∴BD=BC-CD=1,
∴D(1,3).
(2)①由四边形ADEF是矩形,得到∠ADE=90°.
∵点D在线段BE上,∴∠ADB=90°.
∵AD=AO,AB=AB,∠AOB=90°,
∴Rt△ADB≌Rt△AOB(HL).
②由△ADB≌△AOB,得到∠BAD=∠BAO.
在矩形AOBC中,OA∥BC,
∴∠CBA=∠OAB,∴∠BAD=∠CBA,
∴BH=AH,设AH=BH=m,则HC=BC-BH=5-m.
在Rt△ACH中,∵AH2=HC2+AC2,
∴m2=32+(5-m)2,∴m=175,∴BH=175,∴H( 175,3).
(3)S的取值范围是30-3344≤S≤30+3344.
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法正确的是( )
A.对角线相等且互相垂直的四边形是菱形
B.对角线互相平分的四边形是正方形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等且互相平分的四边形是矩形
2.若一个多边形的内角和是外角和的2倍,则它是( )
A.四边形 B.五边形 C.六边形 D.八边形
3.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,且BD=16,则EF=( )
A.32 B.16
C.8 D.4
4.要使四边形ABCD是平行四边形,则∠A∶∠B∶∠C∶∠D可能为( )
A.4∶5∶4∶5 B.3∶4∶5∶6 C.3∶3∶5∶5 D.2∶3∶6∶7
5.若一个菱形的周长是20 cm,两条对角线的比是4∶3,则这个菱形的面积是( )
A.12 cm2 B.24 cm2 C.48 cm2 D.96 cm2
6.如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=100°,则∠DAE的度数为( )
A.10° B.20° C.30° D.40°
第6题图 第7题图 第8题图 第9题图
7.已知?ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
A.∠DAE=∠BAE B.∠DEA=12∠DAB
C.DE=BE D.BC=DE
8.如图,?ABCD的对角线AC,BD相交于点O,点E是AB的中点,△BEO的周长为8,则△BCD的周长为( )
A.8 B.10 C.16 D.20
9.如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
A.75° B.60° C.54° D.67.5°
10.如图,四边形ABCD是矩形,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.若AB=2,则△OEC的面积为( )
A.1 B.2 C.3 D.4
第10题图 第11题图 第12题图
11.如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形 B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形 D.若AD平分∠BAC,则四边形AEDF是菱形
12.如图,在平行四边形ABCD中,∠ABC的平分线BF交AD于点F,FE∥AB.若AB=5,BF=6,则四边形ABEF的面积为( )
A.48 B.35 C.30 D.24
13.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,交AB于点E,连接DF,BF,则∠CDF=( )
A.60° B.65° C.70° D.80°
第13题图 第14题图 第15题图 第16题图
14.如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
A.53 B.35 C.73 D.54
15.如图,在正方形ABCD中,点O是对角线AC的中点,点E是BC边上的一个动点,OF⊥OE交AB边于点F,点G,H分别是点E,F关于AC的对称点,点E从点C运动到点B的过程中,图中阴影部分的面积大小变化情况是( )
A.先增大后减小 B.先减小后增大 C.一直不变 D.不确定
16.如图,在矩形ABCD中,M为CD的中点,连接AM,BM,分别取AM,BM的中点P,Q,以P,Q为顶点作第2个矩形PSRQ,使S,R在AB上.在矩形PSRQ中,重复以上的步骤继续画图.若AM⊥MB,矩形ABCD的周长为30,则第n个矩形的边长分别是( )
A.10×(12)n,5×(12)n B.10×(12)n-1,5×(12)n
C.10×(12)n,5×(12)n-1 D.10×(12)n-1,5×(12)n-1
二、填空题(本大题有3个小题,共12分.17~18小题各3分,19小题有2个空,每空3分)
17.正十边形的外角和为 .?
18.如图,正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为 .?
第18题图 第19题图
19.如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与AD,BC分别相交于点E,F,则四边形AFCE是 ,若AB=6,BC=8,则EF的长为 .?
三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)
如图,在平行四边形ABCD中,过D作DM⊥AB于点M,点N在边CD上,DN=BM,连接AN,BN.
(1)求证:四边形BNDM是矩形.
(2)若CN=3,BN=4,DN=5,求证:AN平分∠DAB.
21.(本小题满分9分)
如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF.
(2)若AB⊥BC,求证:四边形AEOF是正方形.
22.(本小题满分9分)
如图,在△ABC中,∠ABC=90°,∠ACB=30°,O为AC的中点,连接BO并延长到E,使OE=OB,过点A作AD∥BE交CE的延长线于点D.
(1)求证:四边形ABED是平行四边形.
(2)若AB=1 cm,求△ACD的周长.
23. (本小题满分9分)
在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC相交于点D,求证:EF=12(AC-AB);
(2)如图2,请直接写出线段AB,AC,EF之间的数量关系.
24.(本小题满分10分)
如图,四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)若AB=2,CE=2,求CG的长度.
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
25.(本小题满分10分)
如图1,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD的中点,连接AB',C'D,AD',BC',AC',如图2.
(1)求证:四边形AB'C'D是菱形.
(2)四边形ABC'D'的周长为 .?
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形的周长.
26. (本小题满分11分)
在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,按顺时针方向旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(1)如图1,当点D落在BC边上时,求点D的坐标.
(2)如图2,当点D落在线段BE上时,AD与BC交于点H.
①求证:△ADB≌△AOB;
②求点H的坐标.
(3)连接OC,AB,记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
D
C
C
A
B
B
C
C
B
A
D
D
A
A
C
D
17.360° 18.5 19.菱形 152
20. (1)∵四边形ABCD为平行四边形,
∴DC∥AB,∴DN∥BM.
∵DN=BM,∴四边形BNDM是平行四边形.
∵DM⊥AB,∴∠DMB=90°,
∴四边形BNDM是矩形.
(2)由(1)得四边形BNDM是矩形,
∴∠DNB=90°,∴∠BNC=90°.
∵CN=3,BN=4,∴BC=5,∴AD=BC=5.
∵DN=5,∴DN=AD,∴∠DAN=∠DNA.
∵DC∥AB,∴∠DNA=∠NAB,∴∠DAN=∠NAB,
∴AN平分∠DAB.
21. (1)∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD.
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF.
在△BCE和△DCF中,BE=DF,∠B=∠D,BC=DC,
∴△BCE≌△DCF(SAS).
(2)由题意得,OF=12DC,OE=12BC,OE∥BC,∴AE=OE=OF=AF,
∴四边形AEOF是菱形.
∵AB⊥BC,OE∥BC,
∴OE⊥AB,∴∠AEO=90°,
∴四边形AEOF是正方形.
22. (1)如图,连接AE.
∵OA=OC,OB=OE,
∴四边形ABCE是平行四边形,∴CD∥AB.
∵AD∥BE,∴四边形ABED是平行四边形.
(2)∵四边形ABCE是平行四边形,∠ABC=90°,
∴四边形ABCE是矩形,
∴∠BCE=90°.
∵∠ACB=30°,∴∠ACD=60°.
∵AB=CE=ED=1,AC=2AB=2,
∴CD=AC=2,∴△ACD是等边三角形,
∴△ACD的周长为6.
23. (1)∵AE⊥BD,∴∠AED=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠DAE+∠ADE=90°.
∵∠BAE=∠DAE,∴∠ABE=∠ADE,∴AB=AD.
∵AE⊥BD,∴BE=DE,
又∵BF=FC,∴EF=12DC=12(AC-AD)=12(AC-AB).
(2)EF=12(AB-AC).
如图,延长AC交BE的延长线于点P,
∵AE⊥BP,∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°.
∵∠BAE=∠PAE,∴∠ABE=∠APE,
∴AB=AP.
∵AE⊥BP,∴BE=PE,
又∵BF=FC,∴EF=12PC=12(AP-AC)=12(AB-AC).
24. (1)如图1,作EP⊥CD于点P,EQ⊥BC于点Q,
∵∠DCA=∠BCA,EC=EC,
∴△EQC≌△EPC,
∴EQ=EP.
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED.
在Rt△EQF和Rt△EPD中,∠QEF=∠PED,EQ=EP,∠EQF=∠EPD,
∴Rt△EQF≌Rt△EPD,∴EF=ED,
∴矩形DEFG是正方形.
(2)如图2,在Rt△ABC中,AC=2AB=2 2,
∵EC=2,∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=2.
(3)∠EFC=120°或∠EFC=30°.
①当DE与AD的夹角为30°时,∠EFC=120°;
②当DE与DC的夹角为30°时,∠EFC=30°.
综上所述,∠EFC=120°或∠EFC=30°.
25. (1)∵BD是矩形ABCD的对角线,∠ABD=30°,
∴∠ADB=60°,
由平移可得,B'C'=BC=AD,∠D'B'C'=∠DBC=∠ADB=60°,
∴AD∥B'C',∴四边形AB'C'D是平行四边形.
∵B'为BD的中点,
∴在Rt△BAD中,AB'=12BD=DB'.
又∵∠ADB=60°,
∴△ADB'是等边三角形,∴AD=AB',
∴四边形AB'C'D是菱形.
(2)43
由平移可得,AB=C'D',∠ABD'=∠C'D'B=30°,
∴AB∥C'D',∴四边形ABC'D'是平行四边形.
由(1)可得,AC'⊥B'D,∴四边形ABC'D'是菱形.
∵AB=3AD=3,
∴四边形ABC'D'的周长为43.
(3)拼成的矩形的周长是6+3或23+3.
将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,如图所示:
∴拼成的矩形的周长为6+3或2 3+3.
26. (1)∵A(5,0),B(0,3),∴OA=5,OB=3.
∵四边形AOBC是矩形,
∴AC=OB=3,OA=BC=5,∠OBC=∠C=90°.
∵矩形ADEF是由矩形AOBC旋转得到的,∴AD=AO=5.
在Rt△ACD中,CD=AD2-AC2=4,
∴BD=BC-CD=1,
∴D(1,3).
(2)①由四边形ADEF是矩形,得到∠ADE=90°.
∵点D在线段BE上,∴∠ADB=90°.
∵AD=AO,AB=AB,∠AOB=90°,
∴Rt△ADB≌Rt△AOB(HL).
②由△ADB≌△AOB,得到∠BAD=∠BAO.
在矩形AOBC中,OA∥BC,
∴∠CBA=∠OAB,∴∠BAD=∠CBA,
∴BH=AH,设AH=BH=m,则HC=BC-BH=5-m.
在Rt△ACH中,∵AH2=HC2+AC2,
∴m2=32+(5-m)2,∴m=175,∴BH=175,∴H( 175,3).
(3)S的取值范围是30-3344≤S≤30+3344.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
