冀教版八年级数学下册第二十一章 一次函数检测卷综合测试题(Word版 含答案)
文档属性
| 名称 | 冀教版八年级数学下册第二十一章 一次函数检测卷综合测试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 217.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 14:23:10 | ||
图片预览



文档简介
第二十一章 一次函数检测卷
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数中是一次函数的是( )
A.y=x+13 B.y=-1x C.y=2x2-1 D.y=3x+2x2-1
2.函数y=3x+1的图像过点( )
A.(3,5) B.(-2,3) C.(2,7) D.(4,10)
3.已知点A(x1,y1)和点B(x1+1,y2)都在一次函数y=2 019x-2 020的图像上,则下列结论正确的是( )
A.y1>y2 B.y14.不论实数k取何值,一次函数y=kx-3的图像必过的点的坐标为( )
A.(0,-3) B.(0,3) C.(32,0) D.(-32,0)
5.函数y=2x,y=-3x,y=-12x的共同特点是( )
A.图像位于同样的象限 B.y随x的增大而减小
C.y随x的增大而增大 D.图像都过原点
6.在同一直角坐标系中,一次函数y=(k-2)x+k的图像与正比例函数y=kx的图像的位置可能是( )
A B C D
7.已知变量y与x的关系满足下表,那么能反映y与x之间的函数关系式的是( )
x
…
-2
-1
0
1
2
…
y
…
4
3
2
1
0
…
A.y=-2x B.y=x+4 C.y=2x-2 D.y=-x+2
8.对于一次函数y=-2x+4,下列说法错误的是( )
A.函数值随自变量的增大而减小 B.函数的图像不经过第三象限
C.函数的图像与x轴的交点坐标是(0,4) D.函数的图像向下平移4个单位长度得y=-2x的图像
9.若弹簧的总长度y(cm)与所挂重物的质量x(kg)的一次函数关系的图像如图所示,则不挂重物时,弹簧的长度是( )
A.5 cm B.8 cm C.9 cm D.10 cm
10.直线y=2x+2沿x轴向左平移3个单位长度后与y轴的交点坐标是( )
A.(0,2) B.(0,4) C.(0,-4) D.(0,8)
11.已知一次函数y1=kx+b与y2=x+a的图像如图所示,给出下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④x>3时,y1A.1 B.2 C.3 D.4
第11题图 第12题图
12.一次函数y=(k+2)x+1-k的图像如图所示,则使式子3k+1+(1+k)0有意义的k的值可能为( )
A.-2 B.-1 C.0 D.2
13.已知直线y=kx-4(k<0)与两坐标轴所围成的三角形的面积等于4,则直线的表达式为( )
A.y=-2x-4 B.y=-x-4 C.y=-3x-4 D.y=-4x-4
14.如图,在平面直角坐标系中,直线y=23x-23与四边形ABCO的边OC,BC分别交于点E,F.已知∠BCO=90°,OC=4,则△CEF的面积是( )
A.6 B.3 C.12 D.43
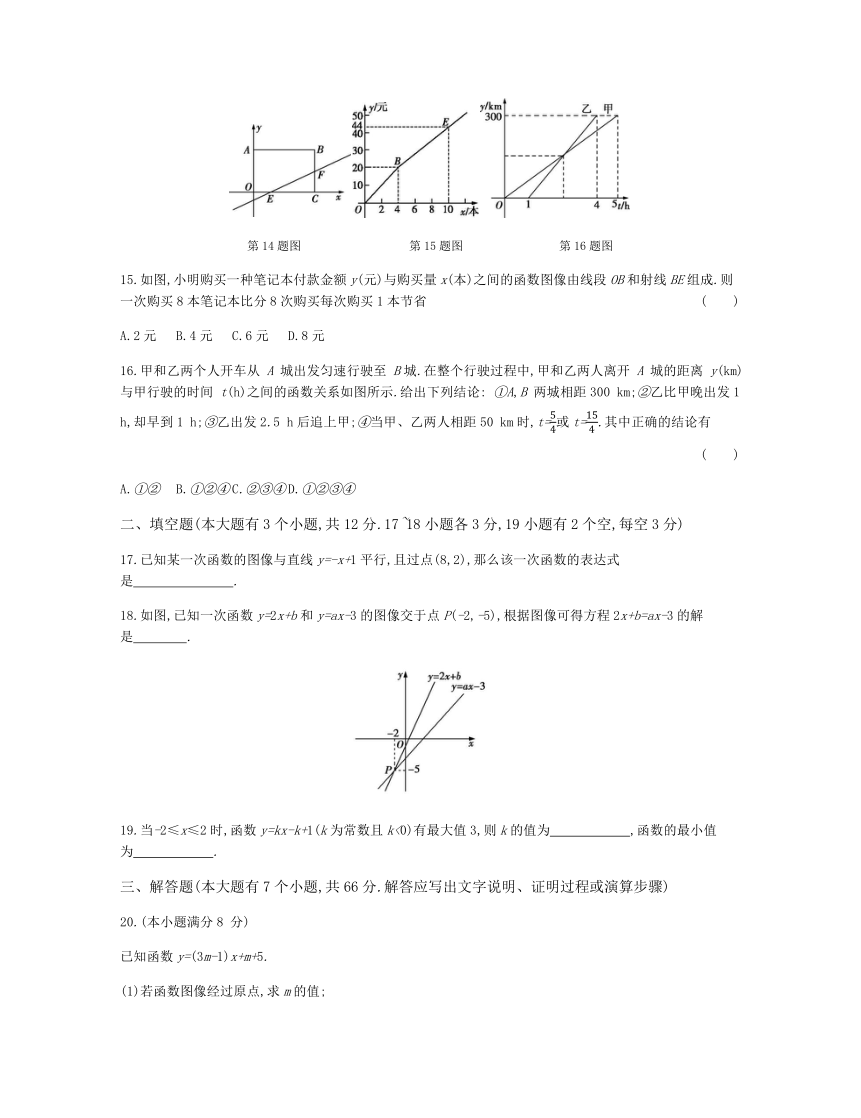
第14题图 第15题图 第16题图
15.如图,小明购买一种笔记本付款金额y(元)与购买量x(本)之间的函数图像由线段OB和射线BE组成.则一次购买8本笔记本比分8次购买每次购买1本节省( )
A.2元 B.4元 C.6元 D.8元
16.甲和乙两个人开车从 A 城出发匀速行驶至 B城.在整个行驶过程中,甲和乙两人离开 A 城的距离 y(km)与甲行驶的时间 t(h)之间的函数关系如图所示.给出下列结论: ①A,B 两城相距300 km;②乙比甲晚出发1 h,却早到1 h;③乙出发2.5 h后追上甲;④当甲、乙两人相距50 km时,t=54或t=154.其中正确的结论有( )
A.①② B.①②④ C.②③④ D.①②③④
二、填空题(本大题有3个小题,共12分.17~18小题各3分,19小题有2个空,每空3分)
17.已知某一次函数的图像与直线y=-x+1平行,且过点(8,2),那么该一次函数的表达式是 .?
18.如图,已知一次函数y=2x+b和y=ax-3的图像交于点P(-2,-5),根据图像可得方程2x+b=ax-3的解是 .?
19.当-2≤x≤2时,函数y=kx-k+1(k为常数且k<0)有最大值3,则k的值为 ,函数的最小值为 .?
三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8 分)
已知函数y=(3m-1)x+m+5.
(1)若函数图像经过原点,求m的值;
(2)若这个函数是一次函数,且y的值随x的值的增大而减小,求m的取值范围.
21.(本小题满分9分)
已知一次函数y=2x-6.
(1)在如图所示的平面直角坐标系中,画出该函数的图像;
(2)判断点(4,3)是否在此函数的图像上;
(3)观察画出的图像,写出当x在什么范围内时y<0.
22.(本小题满分9分)
已知直线l经过A(6,0),B(0,12)两点,且与直线y=x交于点C.
(1)求直线l的表达式;
(2)已知点P(3,0),过点P作直线l的平行线交直线y=x于点D,求△PCD的面积.
23.(本小题满分9分)
某工厂计划生产甲、乙两种产品共2 500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x吨,生产甲、乙两种产品获得的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1 000吨,其他原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
24.(本小题满分10分)
某物流公司引进A,B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5 h,A种机器人于某日0时开始搬运,过了1 h,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(kg)与时间x(时)的函数图像,线段EF表示B种机器人的搬运量yB(kg)与时间x(时)的函数图像.根据图像提供的信息,解答下列问题:
(1)求yB关于x的函数表达式;
(2)如果A,B两种机器人各连续搬运5 h,那么B种机器人比A种机器人多搬运了多少千克?
25.(本小题满分10分)
如图,直线y=kx+6与x轴、y轴分别交于点E,F,点E的坐标为(-8,0),点A 的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内直线y=kx+6上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:在(2)的条件下,当点P运动到什么位置时,△OPA的面积为278?请说明理由.
26.(本小题满分11分)
如图,l1,l2分别表示一种白炽灯和一种节能灯的费用(费用=灯的售价+电费,单位:元)y1,y2与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2 000 h,照明效果一样.
(1)根据图像分别求出l1,l2对应的函数表达式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2 500 h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法.(直接给出答案,不必写出解答过程)
第二十一章
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
A
C
B
A
D
C
D
C
B
D
C
C
A
B
B
A
17.y=-x+10 18.x=-2 19.-23 -1
20. (1)把(0,0)代入y=(3m-1)x+m+5,
得m+5=0,解得m=-5.
(2)因为函数y=(3m-1)x+m+5是一次函数,且y的值随x的值的增大而减小,所以3m-1<0,解得m<13.
21. (1)∵一次函数y=2x-6的图像与两坐标轴的交点坐标分别为(0,-6),(3,0),
∴函数图像如图所示.
(2)∵当x=4时,y=8-6=2≠3,∴该点不在此函数的图像上.
(3)由图可知,当x<3时,y<0.
22. (1)设直线l的表达式为y=kx+b(k≠0),
把A,B两点的坐标分别代入可得6k+b=0,b=12, 解得k=-2,b=12,
∴直线l的表达式为y=-2x+12.
(2)由y=-2x+12,y=x,可得x=4,y=4,
∴C点坐标为(4,4).
设直线PD的表达式为y=-2x+n,
把P(3,0)代入,得-6+n=0,解得n=6,
∴直线PD的表达式为y=-2x+6.
由y=-2x+6,y=x,可得x=2,y=2,
∴D点的坐标为(2,2).
∴S△POD=12×3×2=3,S△POC=12×3×4=6,
∴S△PCD=S△POC-S△POD=6-3=3.
23. (1)由题意,得y=0.3x+0.4(2 500-x)=-0.1x+1 000,
因此y与x之间的函数关系式为y=-0.1x+1 000.
(2)由题意,得0.25x+0.5(2500-x)≤1000,x≤2500,所以1 000≤x≤2 500,
在函数y=-0.1x+1 000中,因为k=-0.1<0,所以y的值随x的值的增大而减小,
所以当x=1 000时,y最大.
2 500-1 000=1 500(吨).
因此生产甲产品1 000吨,乙产品1 500吨时,利润最大.
24. (1)根据题图,设yB关于x的函数表达式为yB=kx+b(k≠0).
将(1,0),(3,180)代入,得k+b=0,3k+b=180,
解得k=90,b=-90.
所以yB关于x的函数表达式为yB=90x-90(1≤x≤6).
(2)根据题图,设yA关于x的函数表达式为yA=k1x(k1≠0).
根据题意,得3k1=180,解得k1=60.
所以yA=60x(0≤x≤5).
当x=5时,yA=60×5=300.
当x=6时,yB=90×6-90=450.
450-300=150(kg).
答:如果A,B两种机器人各连续搬运5 h,那么B种机器人比A种机器人多搬运了150 kg.
25. (1)因为直线y=kx+6与x轴交于点E(-8,0),
所以-8k+6=0,解得k=34.
(2)过点P作PH⊥x轴于点H.
因为点A的坐标为(-6,0),所以AO=6.
因为点P(x,y)是第二象限内直线y=34x+6上的一个动点,
所以PH=y=34x+6,
所以S=12AO×PH=12×6×(34x+6)=94x+18(-8 (3)当点P的坐标为(-132,98)时,△OPA的面积为278.理由如下:
当S=278时,94x+18=278,解得x=-132,
此时y=34×(-132)+6=98.
所以当点P的坐标为(-132,98)时,△OPA的面积为278.
26. (1)设l1的函数表达式为y1=k1x+b1(k1≠0),l2的函数表达式为y2=k2x+b2(k2≠0).
由题图可知l1过点(0,2),(500,17),
∴b1=2,500k1+b1=17,∴k1=0.03,b1=2,
∴y1=0.03x+2(0≤x≤2 000).
由l2过点(0,20),(500,26),
同理可得y2=0.012x+20(0≤x≤2 000).
(2)由y1=y2,得x=1 000,
∴当照明时间为1 000 h时,两种灯的费用相同.
(3)先用节能灯2 000 h,再用白炽灯500 h.(或先用白炽灯500 h,再用节能灯2 000 h)
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数中是一次函数的是( )
A.y=x+13 B.y=-1x C.y=2x2-1 D.y=3x+2x2-1
2.函数y=3x+1的图像过点( )
A.(3,5) B.(-2,3) C.(2,7) D.(4,10)
3.已知点A(x1,y1)和点B(x1+1,y2)都在一次函数y=2 019x-2 020的图像上,则下列结论正确的是( )
A.y1>y2 B.y1
A.(0,-3) B.(0,3) C.(32,0) D.(-32,0)
5.函数y=2x,y=-3x,y=-12x的共同特点是( )
A.图像位于同样的象限 B.y随x的增大而减小
C.y随x的增大而增大 D.图像都过原点
6.在同一直角坐标系中,一次函数y=(k-2)x+k的图像与正比例函数y=kx的图像的位置可能是( )
A B C D
7.已知变量y与x的关系满足下表,那么能反映y与x之间的函数关系式的是( )
x
…
-2
-1
0
1
2
…
y
…
4
3
2
1
0
…
A.y=-2x B.y=x+4 C.y=2x-2 D.y=-x+2
8.对于一次函数y=-2x+4,下列说法错误的是( )
A.函数值随自变量的增大而减小 B.函数的图像不经过第三象限
C.函数的图像与x轴的交点坐标是(0,4) D.函数的图像向下平移4个单位长度得y=-2x的图像
9.若弹簧的总长度y(cm)与所挂重物的质量x(kg)的一次函数关系的图像如图所示,则不挂重物时,弹簧的长度是( )
A.5 cm B.8 cm C.9 cm D.10 cm
10.直线y=2x+2沿x轴向左平移3个单位长度后与y轴的交点坐标是( )
A.(0,2) B.(0,4) C.(0,-4) D.(0,8)
11.已知一次函数y1=kx+b与y2=x+a的图像如图所示,给出下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④x>3时,y1
第11题图 第12题图
12.一次函数y=(k+2)x+1-k的图像如图所示,则使式子3k+1+(1+k)0有意义的k的值可能为( )
A.-2 B.-1 C.0 D.2
13.已知直线y=kx-4(k<0)与两坐标轴所围成的三角形的面积等于4,则直线的表达式为( )
A.y=-2x-4 B.y=-x-4 C.y=-3x-4 D.y=-4x-4
14.如图,在平面直角坐标系中,直线y=23x-23与四边形ABCO的边OC,BC分别交于点E,F.已知∠BCO=90°,OC=4,则△CEF的面积是( )
A.6 B.3 C.12 D.43
第14题图 第15题图 第16题图
15.如图,小明购买一种笔记本付款金额y(元)与购买量x(本)之间的函数图像由线段OB和射线BE组成.则一次购买8本笔记本比分8次购买每次购买1本节省( )
A.2元 B.4元 C.6元 D.8元
16.甲和乙两个人开车从 A 城出发匀速行驶至 B城.在整个行驶过程中,甲和乙两人离开 A 城的距离 y(km)与甲行驶的时间 t(h)之间的函数关系如图所示.给出下列结论: ①A,B 两城相距300 km;②乙比甲晚出发1 h,却早到1 h;③乙出发2.5 h后追上甲;④当甲、乙两人相距50 km时,t=54或t=154.其中正确的结论有( )
A.①② B.①②④ C.②③④ D.①②③④
二、填空题(本大题有3个小题,共12分.17~18小题各3分,19小题有2个空,每空3分)
17.已知某一次函数的图像与直线y=-x+1平行,且过点(8,2),那么该一次函数的表达式是 .?
18.如图,已知一次函数y=2x+b和y=ax-3的图像交于点P(-2,-5),根据图像可得方程2x+b=ax-3的解是 .?
19.当-2≤x≤2时,函数y=kx-k+1(k为常数且k<0)有最大值3,则k的值为 ,函数的最小值为 .?
三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8 分)
已知函数y=(3m-1)x+m+5.
(1)若函数图像经过原点,求m的值;
(2)若这个函数是一次函数,且y的值随x的值的增大而减小,求m的取值范围.
21.(本小题满分9分)
已知一次函数y=2x-6.
(1)在如图所示的平面直角坐标系中,画出该函数的图像;
(2)判断点(4,3)是否在此函数的图像上;
(3)观察画出的图像,写出当x在什么范围内时y<0.
22.(本小题满分9分)
已知直线l经过A(6,0),B(0,12)两点,且与直线y=x交于点C.
(1)求直线l的表达式;
(2)已知点P(3,0),过点P作直线l的平行线交直线y=x于点D,求△PCD的面积.
23.(本小题满分9分)
某工厂计划生产甲、乙两种产品共2 500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x吨,生产甲、乙两种产品获得的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1 000吨,其他原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
24.(本小题满分10分)
某物流公司引进A,B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5 h,A种机器人于某日0时开始搬运,过了1 h,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(kg)与时间x(时)的函数图像,线段EF表示B种机器人的搬运量yB(kg)与时间x(时)的函数图像.根据图像提供的信息,解答下列问题:
(1)求yB关于x的函数表达式;
(2)如果A,B两种机器人各连续搬运5 h,那么B种机器人比A种机器人多搬运了多少千克?
25.(本小题满分10分)
如图,直线y=kx+6与x轴、y轴分别交于点E,F,点E的坐标为(-8,0),点A 的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内直线y=kx+6上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:在(2)的条件下,当点P运动到什么位置时,△OPA的面积为278?请说明理由.
26.(本小题满分11分)
如图,l1,l2分别表示一种白炽灯和一种节能灯的费用(费用=灯的售价+电费,单位:元)y1,y2与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2 000 h,照明效果一样.
(1)根据图像分别求出l1,l2对应的函数表达式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2 500 h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法.(直接给出答案,不必写出解答过程)
第二十一章
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
A
C
B
A
D
C
D
C
B
D
C
C
A
B
B
A
17.y=-x+10 18.x=-2 19.-23 -1
20. (1)把(0,0)代入y=(3m-1)x+m+5,
得m+5=0,解得m=-5.
(2)因为函数y=(3m-1)x+m+5是一次函数,且y的值随x的值的增大而减小,所以3m-1<0,解得m<13.
21. (1)∵一次函数y=2x-6的图像与两坐标轴的交点坐标分别为(0,-6),(3,0),
∴函数图像如图所示.
(2)∵当x=4时,y=8-6=2≠3,∴该点不在此函数的图像上.
(3)由图可知,当x<3时,y<0.
22. (1)设直线l的表达式为y=kx+b(k≠0),
把A,B两点的坐标分别代入可得6k+b=0,b=12, 解得k=-2,b=12,
∴直线l的表达式为y=-2x+12.
(2)由y=-2x+12,y=x,可得x=4,y=4,
∴C点坐标为(4,4).
设直线PD的表达式为y=-2x+n,
把P(3,0)代入,得-6+n=0,解得n=6,
∴直线PD的表达式为y=-2x+6.
由y=-2x+6,y=x,可得x=2,y=2,
∴D点的坐标为(2,2).
∴S△POD=12×3×2=3,S△POC=12×3×4=6,
∴S△PCD=S△POC-S△POD=6-3=3.
23. (1)由题意,得y=0.3x+0.4(2 500-x)=-0.1x+1 000,
因此y与x之间的函数关系式为y=-0.1x+1 000.
(2)由题意,得0.25x+0.5(2500-x)≤1000,x≤2500,所以1 000≤x≤2 500,
在函数y=-0.1x+1 000中,因为k=-0.1<0,所以y的值随x的值的增大而减小,
所以当x=1 000时,y最大.
2 500-1 000=1 500(吨).
因此生产甲产品1 000吨,乙产品1 500吨时,利润最大.
24. (1)根据题图,设yB关于x的函数表达式为yB=kx+b(k≠0).
将(1,0),(3,180)代入,得k+b=0,3k+b=180,
解得k=90,b=-90.
所以yB关于x的函数表达式为yB=90x-90(1≤x≤6).
(2)根据题图,设yA关于x的函数表达式为yA=k1x(k1≠0).
根据题意,得3k1=180,解得k1=60.
所以yA=60x(0≤x≤5).
当x=5时,yA=60×5=300.
当x=6时,yB=90×6-90=450.
450-300=150(kg).
答:如果A,B两种机器人各连续搬运5 h,那么B种机器人比A种机器人多搬运了150 kg.
25. (1)因为直线y=kx+6与x轴交于点E(-8,0),
所以-8k+6=0,解得k=34.
(2)过点P作PH⊥x轴于点H.
因为点A的坐标为(-6,0),所以AO=6.
因为点P(x,y)是第二象限内直线y=34x+6上的一个动点,
所以PH=y=34x+6,
所以S=12AO×PH=12×6×(34x+6)=94x+18(-8
当S=278时,94x+18=278,解得x=-132,
此时y=34×(-132)+6=98.
所以当点P的坐标为(-132,98)时,△OPA的面积为278.
26. (1)设l1的函数表达式为y1=k1x+b1(k1≠0),l2的函数表达式为y2=k2x+b2(k2≠0).
由题图可知l1过点(0,2),(500,17),
∴b1=2,500k1+b1=17,∴k1=0.03,b1=2,
∴y1=0.03x+2(0≤x≤2 000).
由l2过点(0,20),(500,26),
同理可得y2=0.012x+20(0≤x≤2 000).
(2)由y1=y2,得x=1 000,
∴当照明时间为1 000 h时,两种灯的费用相同.
(3)先用节能灯2 000 h,再用白炽灯500 h.(或先用白炽灯500 h,再用节能灯2 000 h)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
