冀教版八年级数学下册第二十章 函数 检测卷(word版 含答案)
文档属性
| 名称 | 冀教版八年级数学下册第二十章 函数 检测卷(word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 274.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 14:18:33 | ||
图片预览


文档简介
第二十章 函数
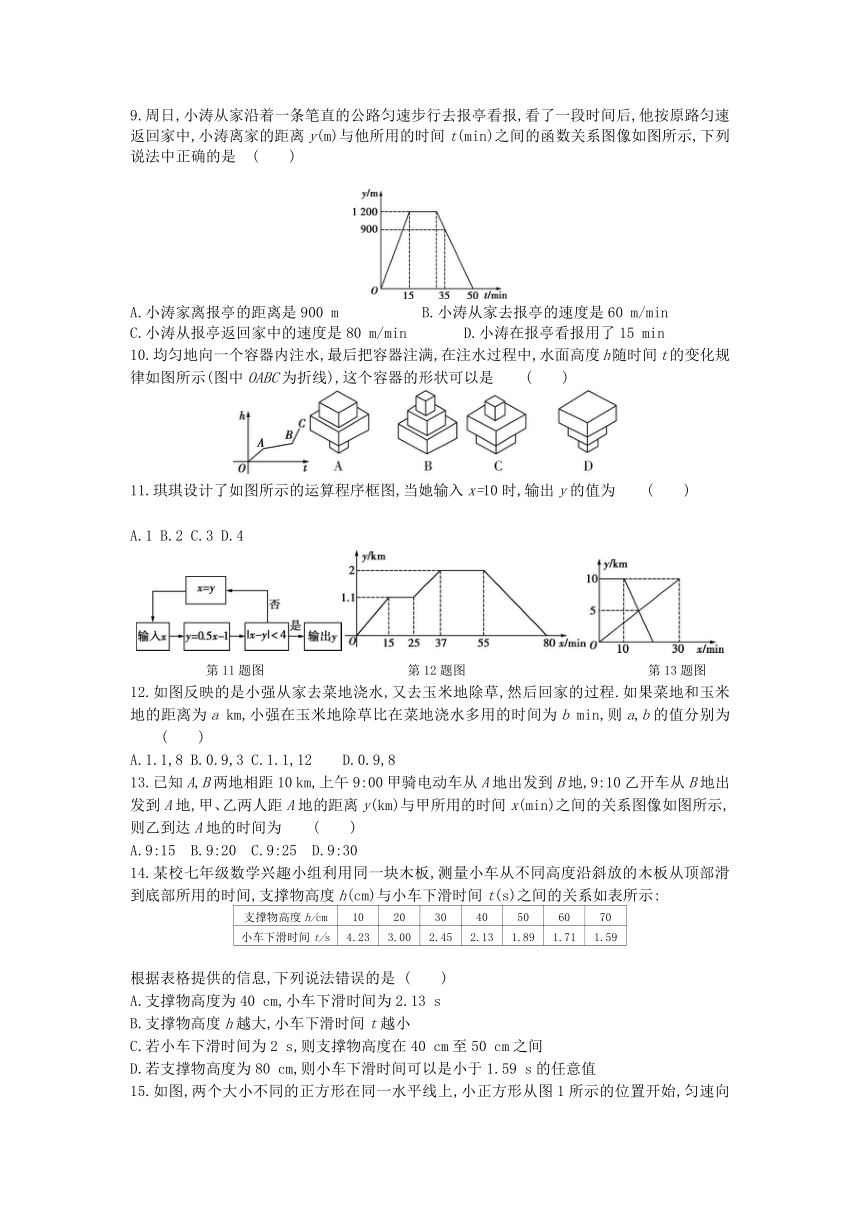
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在圆的面积公式S=πR2中,变量是 ( )
A.S B.R C.π和R D.S和R
2.下列曲线都表示变量y与变量x之间的对应关系,其中不能看作y是x的函数的是 ( )
3.函数y=中自变量x的取值范围是 ( )
A.x≥-2 B.x>-2 C.x≤-2 D.x<-2
4.下列变量间的关系不是函数关系的是 ( )
A.长方形的长一定,其宽与面积 B.正方形的周长与面积
C.等腰三角形的底边长与面积 D.圆的周长与半径
5.下表列出了一项试验的统计数据,表示的是皮球从高处落下时,弹跳高度b与下降高度d的关系,下列能表示这个函数关系的式子是 ( )
d
50
80
100
150
b
25
40
50
75
A.b=d2 B.b=2d C.b= D.b=d+25
6.小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校.小明从家到学校行驶路程s(m)与时间t(min)的大致图像是 ( )
7.有一段导线,在0 ℃时电阻为2 Ω,温度每增加1 ℃,电阻增加0.008 Ω,那么电阻R(Ω)与温度T(℃)之间的函数关系式为 ( )
A.R=2+0.008T B.R=2-0.008T C.T=2+0.008R D.T=2-0.008R
8.“龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它在途中睡觉,而乌龟一直坚持爬行,最终赢得比赛,下列函数图像可以体现这一比赛过程的是 ( )
9.周日,小涛从家沿着一条笔直的公路匀速步行去报亭看报,看了一段时间后,他按原路匀速返回家中,小涛离家的距离y(m)与他所用的时间t(min)之间的函数关系图像如图所示,下列说法中正确的是 ( )
A.小涛家离报亭的距离是900 m B.小涛从家去报亭的速度是60 m/min
C.小涛从报亭返回家中的速度是80 m/min D.小涛在报亭看报用了15 min
10.均匀地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是 ( )
11.琪琪设计了如图所示的运算程序框图,当她输入x=10时,输出y的值为 ( )
A.1 B.2 C.3 D.4
第11题图 第12题图 第13题图
12.如图反映的是小强从家去菜地浇水,又去玉米地除草,然后回家的过程.如果菜地和玉米地的距离为a km,小强在玉米地除草比在菜地浇水多用的时间为b min,则a,b的值分别为 ( )
A.1.1,8 B.0.9,3 C.1.1,12 D.0.9,8
13.已知A,B两地相距10 km,上午9:00甲骑电动车从A地出发到B地,9:10乙开车从B地出发到A地,甲、乙两人距A地的距离y(km)与甲所用的时间x(min)之间的关系图像如图所示,则乙到达A地的时间为 ( )
A.9:15 B.9:20 C.9:25 D.9:30
14.某校七年级数学兴趣小组利用同一块木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间,支撑物高度h(cm)与小车下滑时间t(s)之间的关系如表所示:
支撑物高度h/cm
10
20
30
40
50
60
70
小车下滑时间t/s
4.23
3.00
2.45
2.13
1.89
1.71
1.59
根据表格提供的信息,下列说法错误的是 ( )
A.支撑物高度为40 cm,小车下滑时间为2.13 s
B.支撑物高度h越大,小车下滑时间t越小
C.若小车下滑时间为2 s,则支撑物高度在40 cm至50 cm之间
D.若支撑物高度为80 cm,则小车下滑时间可以是小于1.59 s的任意值
15.如图,两个大小不同的正方形在同一水平线上,小正方形从图1所示的位置开始,匀速向右平移,到图3所示的位置停止运动.如果设运动时间为x,两个正方形重叠部分的面积为y,则能表示y与x之间函数关系的大致图像的是 ( )
A B C D
16.甲、乙两人在直线跑道上同起点、同终点匀速跑步500 m,先到终点的人原地休息.已知甲先出发2 s,在跑步过程中,甲、乙两人之间的距离y(m)与乙出发的时间t(s)之间的函数关系图像如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的结论是 ( )
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题有3个小题,共12分.17~18小题各3分,19小题有2个空,每空3分)
17.某市冬季某一天的气温变化曲线如图所示,其中变量有 .?
第17题图 第19题图
18.在百米跑道上,小亮正以8 m/s的速度匀速向前奔跑,则他距终点的路程s(m)与奔跑时间t(s)之间的函数关系式及自变量t的取值范围为 .?
19.如图1,一种圆环的外圆直径是8 cm,环宽1 cm.如图2,若把2个这样的圆环扣在一起并拉紧,则其长度为 cm;如图3,若把x个这样的圆环扣在一起并拉紧,其长度为y cm,则y与x之间的函数关系式是 .?
三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)
指出下列各关系式中的常量、变量及自变量的取值范围.
(1)学校游泳池盛满水2 400立方米,出水管每分钟可放水30立方米,打开出水管,一直到放尽为止,则游泳池内水量W(立方米)与放水时间t(分)的函数关系式是W=2 400-30t;
(2)若数学练习本每本0.8元,则所付款数y与所买练习本的本数x之间的函数关系式是y=0.8x.
21.(本小题满分8分)
图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的函数关系图像如图2所示.
(1)根据图2填表:
x/min
0
3
6
8
12
…
y/m
…
(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.
22.(本小题满分8分)
一辆汽车的油箱中有汽油50 L,如果不再加油,那么油箱中的剩余油量y(L)随行驶路程x(km)的增加而减少,平均耗油量为0.1 L/km.
(1)写出y与x之间的函数关系式;
(2)写出自变量x的取值范围;
(3)当汽车行驶200 km时,油箱中还有多少汽油?
23.(本小题满分10分)
某市自来水公司为了鼓励市民节约用水,采取分段收费标准,居民每月应缴水费y(元)是用水量x(吨)的函数,当0≤x≤5时,y=0.72x;当x>5时,y=0.9x-0.9.
(1)画出函数的图像;
(2)观察(1)中的图像,利用函数关系式,说明该自来水公司采取的收费标准.
24.(本小题满分10分)
某天早晨,王老师从家出发,驾车前往学校,途中在路旁一家饭店吃早餐,如图所示是王老师从家到学校这一过程中行驶路程s(km)与时间t(min)之间的关系.
(1)学校离王老师家有多远?王老师从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快速度为多少?
25.(本小题满分10分)
某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3 000元;另一部分是按月销售量确定的奖励工资,每销售一件产品,奖励工资10元.设某销售员销售产品x件,他应得工资记为y元.
(1)求y与x的函数关系式;
(2)该销售员的工资为4 100元,他这个月销售了多少件产品?
(3)要使每月工资超过4 500元,则每月的销售量应当超过多少件?
26.(本小题满分12分)
如图1,正方形ABCD的边长为4 cm,E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E,向终点E以a cm/s的速度匀速运动,设运动时间为t(s),△PBF的面积记为S(cm2).S与t之间的部分函数图像如图2所示,已知点M(1,),N(5,6)在S与t的函数图像上.
(1)求线段BF的长及a的值;
(2)写出S与t的函数关系式,并补全该函数图像;
(3)当t为多少时,△PBF的面积S为4 cm2?
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
D
C
B
C
C
C
A
B
D
C
A
D
B
D
C
D
17.温度、时间 18.s=100-8t,0≤t≤12.5
19.14 y=6x+2
20. (1)变量有W,t,常量有2 400,-30,
自变量t的取值范围是0≤t≤80.
(2)变量有x,y,常量有0.8,
自变量x的取值范围是全体自然数.
21. (1)填表如下:
x/min
0
3
6
8
12
…
y/m
5
70
5
54
5
…
(2)是.因为每给定一个x的值都有唯一确定的函数值y与之对应,符合函数的定义,所以变量y是x的函数.
(3)因为最高点为70 m,最低点为5 m,所以摩天轮的直径为65 m.
22. (1)根据题意可知,当汽车行驶x km时,耗油量为0.1x L,
所以剩余油量y=50-0.1x,即y与x之间的函数关系式为y=50-0.1x.
(2)当y=0时,x==500,
所以自变量x的取值范围是0≤x≤500.
(3)当x=200时,y=50-20=30,
所以当汽车行驶200 km时,油箱中还有30 L汽油.
23. (1)函数图像如图所示.
(2)由(1)中的图像可得,当0≤x≤5时,用水收费标准为每吨0.72元,当x>5时,用水量超出5吨的部分每吨0.9元.
24. (1)学校离王老师家10 km,王老师从出发到学校,用了25 min.
(2)王老师吃早餐用了20-10=10(min).
(3)王老师吃早餐以前的速度为5÷10=0.5(km/min),
王老师吃完早餐以后的速度为(10-5)÷(25-20)=1(km/min),
所以王老师吃完早餐以后的速度快,最快速度为1 km/min.
25. (1)由题意可知,y=10x+3 000(x≥0,且x为整数).
(2)因为该销售员的工资为4 100元,
所以10x+3 000=4 100,解得x=110,
所以该销售员的工资为4 100元,他这个月销售了110件产品.
(3)根据题意可得,10x+3 000>4 500,解得x>150,
所以要使每月工资超过4 500元,则每月的销售量应当超过150件.
26. (1)根据题意可知,当点P在CD边上时,△PBF的面积S=6 cm2,
则有BF×4=6,解得BF=3 cm,
当t=1 s时,S= cm2,BP=a cm,
则有BF×BP=,即a=,解得a=1,
故线段BF的长为3 cm,a的值为1.
(2)由(1)可知,a=1,BF=3 cm,
因为BC=CD=4 cm,DE=2 cm,
所以当0≤t≤4时,S=×BF×BP=×3×t=t;
当4当8综上,S=
函数图像如图所示.
(3)当0≤t≤4时,t=4,t=,符合题意;
当8故当t=或t=时,△PBF的面积S为4 cm2.
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在圆的面积公式S=πR2中,变量是 ( )
A.S B.R C.π和R D.S和R
2.下列曲线都表示变量y与变量x之间的对应关系,其中不能看作y是x的函数的是 ( )
3.函数y=中自变量x的取值范围是 ( )
A.x≥-2 B.x>-2 C.x≤-2 D.x<-2
4.下列变量间的关系不是函数关系的是 ( )
A.长方形的长一定,其宽与面积 B.正方形的周长与面积
C.等腰三角形的底边长与面积 D.圆的周长与半径
5.下表列出了一项试验的统计数据,表示的是皮球从高处落下时,弹跳高度b与下降高度d的关系,下列能表示这个函数关系的式子是 ( )
d
50
80
100
150
b
25
40
50
75
A.b=d2 B.b=2d C.b= D.b=d+25
6.小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校.小明从家到学校行驶路程s(m)与时间t(min)的大致图像是 ( )
7.有一段导线,在0 ℃时电阻为2 Ω,温度每增加1 ℃,电阻增加0.008 Ω,那么电阻R(Ω)与温度T(℃)之间的函数关系式为 ( )
A.R=2+0.008T B.R=2-0.008T C.T=2+0.008R D.T=2-0.008R
8.“龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它在途中睡觉,而乌龟一直坚持爬行,最终赢得比赛,下列函数图像可以体现这一比赛过程的是 ( )
9.周日,小涛从家沿着一条笔直的公路匀速步行去报亭看报,看了一段时间后,他按原路匀速返回家中,小涛离家的距离y(m)与他所用的时间t(min)之间的函数关系图像如图所示,下列说法中正确的是 ( )
A.小涛家离报亭的距离是900 m B.小涛从家去报亭的速度是60 m/min
C.小涛从报亭返回家中的速度是80 m/min D.小涛在报亭看报用了15 min
10.均匀地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是 ( )
11.琪琪设计了如图所示的运算程序框图,当她输入x=10时,输出y的值为 ( )
A.1 B.2 C.3 D.4
第11题图 第12题图 第13题图
12.如图反映的是小强从家去菜地浇水,又去玉米地除草,然后回家的过程.如果菜地和玉米地的距离为a km,小强在玉米地除草比在菜地浇水多用的时间为b min,则a,b的值分别为 ( )
A.1.1,8 B.0.9,3 C.1.1,12 D.0.9,8
13.已知A,B两地相距10 km,上午9:00甲骑电动车从A地出发到B地,9:10乙开车从B地出发到A地,甲、乙两人距A地的距离y(km)与甲所用的时间x(min)之间的关系图像如图所示,则乙到达A地的时间为 ( )
A.9:15 B.9:20 C.9:25 D.9:30
14.某校七年级数学兴趣小组利用同一块木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间,支撑物高度h(cm)与小车下滑时间t(s)之间的关系如表所示:
支撑物高度h/cm
10
20
30
40
50
60
70
小车下滑时间t/s
4.23
3.00
2.45
2.13
1.89
1.71
1.59
根据表格提供的信息,下列说法错误的是 ( )
A.支撑物高度为40 cm,小车下滑时间为2.13 s
B.支撑物高度h越大,小车下滑时间t越小
C.若小车下滑时间为2 s,则支撑物高度在40 cm至50 cm之间
D.若支撑物高度为80 cm,则小车下滑时间可以是小于1.59 s的任意值
15.如图,两个大小不同的正方形在同一水平线上,小正方形从图1所示的位置开始,匀速向右平移,到图3所示的位置停止运动.如果设运动时间为x,两个正方形重叠部分的面积为y,则能表示y与x之间函数关系的大致图像的是 ( )
A B C D
16.甲、乙两人在直线跑道上同起点、同终点匀速跑步500 m,先到终点的人原地休息.已知甲先出发2 s,在跑步过程中,甲、乙两人之间的距离y(m)与乙出发的时间t(s)之间的函数关系图像如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的结论是 ( )
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题有3个小题,共12分.17~18小题各3分,19小题有2个空,每空3分)
17.某市冬季某一天的气温变化曲线如图所示,其中变量有 .?
第17题图 第19题图
18.在百米跑道上,小亮正以8 m/s的速度匀速向前奔跑,则他距终点的路程s(m)与奔跑时间t(s)之间的函数关系式及自变量t的取值范围为 .?
19.如图1,一种圆环的外圆直径是8 cm,环宽1 cm.如图2,若把2个这样的圆环扣在一起并拉紧,则其长度为 cm;如图3,若把x个这样的圆环扣在一起并拉紧,其长度为y cm,则y与x之间的函数关系式是 .?
三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)
指出下列各关系式中的常量、变量及自变量的取值范围.
(1)学校游泳池盛满水2 400立方米,出水管每分钟可放水30立方米,打开出水管,一直到放尽为止,则游泳池内水量W(立方米)与放水时间t(分)的函数关系式是W=2 400-30t;
(2)若数学练习本每本0.8元,则所付款数y与所买练习本的本数x之间的函数关系式是y=0.8x.
21.(本小题满分8分)
图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的函数关系图像如图2所示.
(1)根据图2填表:
x/min
0
3
6
8
12
…
y/m
…
(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.
22.(本小题满分8分)
一辆汽车的油箱中有汽油50 L,如果不再加油,那么油箱中的剩余油量y(L)随行驶路程x(km)的增加而减少,平均耗油量为0.1 L/km.
(1)写出y与x之间的函数关系式;
(2)写出自变量x的取值范围;
(3)当汽车行驶200 km时,油箱中还有多少汽油?
23.(本小题满分10分)
某市自来水公司为了鼓励市民节约用水,采取分段收费标准,居民每月应缴水费y(元)是用水量x(吨)的函数,当0≤x≤5时,y=0.72x;当x>5时,y=0.9x-0.9.
(1)画出函数的图像;
(2)观察(1)中的图像,利用函数关系式,说明该自来水公司采取的收费标准.
24.(本小题满分10分)
某天早晨,王老师从家出发,驾车前往学校,途中在路旁一家饭店吃早餐,如图所示是王老师从家到学校这一过程中行驶路程s(km)与时间t(min)之间的关系.
(1)学校离王老师家有多远?王老师从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快速度为多少?
25.(本小题满分10分)
某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3 000元;另一部分是按月销售量确定的奖励工资,每销售一件产品,奖励工资10元.设某销售员销售产品x件,他应得工资记为y元.
(1)求y与x的函数关系式;
(2)该销售员的工资为4 100元,他这个月销售了多少件产品?
(3)要使每月工资超过4 500元,则每月的销售量应当超过多少件?
26.(本小题满分12分)
如图1,正方形ABCD的边长为4 cm,E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E,向终点E以a cm/s的速度匀速运动,设运动时间为t(s),△PBF的面积记为S(cm2).S与t之间的部分函数图像如图2所示,已知点M(1,),N(5,6)在S与t的函数图像上.
(1)求线段BF的长及a的值;
(2)写出S与t的函数关系式,并补全该函数图像;
(3)当t为多少时,△PBF的面积S为4 cm2?
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
D
C
B
C
C
C
A
B
D
C
A
D
B
D
C
D
17.温度、时间 18.s=100-8t,0≤t≤12.5
19.14 y=6x+2
20. (1)变量有W,t,常量有2 400,-30,
自变量t的取值范围是0≤t≤80.
(2)变量有x,y,常量有0.8,
自变量x的取值范围是全体自然数.
21. (1)填表如下:
x/min
0
3
6
8
12
…
y/m
5
70
5
54
5
…
(2)是.因为每给定一个x的值都有唯一确定的函数值y与之对应,符合函数的定义,所以变量y是x的函数.
(3)因为最高点为70 m,最低点为5 m,所以摩天轮的直径为65 m.
22. (1)根据题意可知,当汽车行驶x km时,耗油量为0.1x L,
所以剩余油量y=50-0.1x,即y与x之间的函数关系式为y=50-0.1x.
(2)当y=0时,x==500,
所以自变量x的取值范围是0≤x≤500.
(3)当x=200时,y=50-20=30,
所以当汽车行驶200 km时,油箱中还有30 L汽油.
23. (1)函数图像如图所示.
(2)由(1)中的图像可得,当0≤x≤5时,用水收费标准为每吨0.72元,当x>5时,用水量超出5吨的部分每吨0.9元.
24. (1)学校离王老师家10 km,王老师从出发到学校,用了25 min.
(2)王老师吃早餐用了20-10=10(min).
(3)王老师吃早餐以前的速度为5÷10=0.5(km/min),
王老师吃完早餐以后的速度为(10-5)÷(25-20)=1(km/min),
所以王老师吃完早餐以后的速度快,最快速度为1 km/min.
25. (1)由题意可知,y=10x+3 000(x≥0,且x为整数).
(2)因为该销售员的工资为4 100元,
所以10x+3 000=4 100,解得x=110,
所以该销售员的工资为4 100元,他这个月销售了110件产品.
(3)根据题意可得,10x+3 000>4 500,解得x>150,
所以要使每月工资超过4 500元,则每月的销售量应当超过150件.
26. (1)根据题意可知,当点P在CD边上时,△PBF的面积S=6 cm2,
则有BF×4=6,解得BF=3 cm,
当t=1 s时,S= cm2,BP=a cm,
则有BF×BP=,即a=,解得a=1,
故线段BF的长为3 cm,a的值为1.
(2)由(1)可知,a=1,BF=3 cm,
因为BC=CD=4 cm,DE=2 cm,
所以当0≤t≤4时,S=×BF×BP=×3×t=t;
当4
函数图像如图所示.
(3)当0≤t≤4时,t=4,t=,符合题意;
当8
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
