冀教版八年级数学下册第十九章平面直角坐标系综合能力检测卷(Word版 含答案)
文档属性
| 名称 | 冀教版八年级数学下册第十九章平面直角坐标系综合能力检测卷(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 351.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 14:24:32 | ||
图片预览



文档简介
第十九章 综合能力检测卷
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.以下描述中,能确定具体位置的是 ( )
A.万达电影院2排 B.距唐山高铁站2 km
C.北偏东30° D.东经106°,北纬31°
2.如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为 ( )
A.(2,2) B.(2,3)
C.(3,2) D.(0,3)
3.已知古塔在嘉淇的北偏东30°方向,且距离嘉淇2 km,符合条件的示意图是 ( )
4.下列各点中,通过上下平移不能与点(2,-1)重合的是 ( )
A.(-2,-1) B.(2,-2) C.(2,0) D.(2,-3)
5.已知点A(1,2)与点B(-1,a)关于原点对称,则a的值为 ( )
A.1 B.2 C.-1 D.-2
6.若点P(a,b)在第三象限,则点M(-a+2,b-3)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知平面直角坐标系中,长方形ABCD上各点的横坐标不变,纵坐标分别乘,则所得图形相当于将原图形 ( )
A.横向压缩为原来的 B.纵向压缩为原来的
C.横向拉长为原来的2倍 D.纵向压缩为原来的2倍
8.已知平面直角坐标系中点A的坐标为(-4,3),则下列结论正确的是 ( )
A.点A到x轴的距离为4
B.点A到y轴的距离为3
C.点A到原点的距离为5
D.点A关于x轴对称的点的坐标为(4,-3)
9.已知△ABC在平面直角坐标系中的位置如图所示,若△A'B'C'与△ABC关于y轴对称,则点A的对应点A'的坐标是 ( )
A.(3,2) B.(3,-2)
C.(2,3) D.(2,-3)
10.将点P(2m+3,m-2)向上平移1个单位长度后得到点P',且点P'在x轴上,那么点P的坐标是 ( )
A.(9,1) B.(5,-1) C.(7,0) D.(1,-3)
11.平面直角坐标系中的四边形ABCD,各顶点的横、纵坐标均扩大为原来的2倍,则下列说法正确的是 ( )
A.四边形ABCD的形状改变,面积变为原来的2倍
B.四边形ABCD的形状不变,面积变为原来的2倍
C.四边形ABCD的形状改变,面积变为原来的4倍
D.四边形ABCD的形状不变,面积变为原来的4倍
12.如图是A,B,C,D四位同学的家所在的位置,若以A同学家的位置为坐标原点建立平面直角坐标系,且C同学家的位置的坐标为(1,5),则B,D同学家的坐标分别为 ( )
A.(2,3),(3,2) B.(3,2),(2,3)
C.(3,2),(-2,3) D.(2,3),(-3,2)
第12题图 第13题图 第14题图
13.已知图1中的△ABC经过一定的变换后得到图2中的△A'B'C',如果图1中△ABC上的点P的坐标为(a,b),那么点P在图2中的对应点P'的坐标为 ( )
A.(a-2,b-3) B.(a-3,b-2) C.(a+3,b+2) D.(a+2,b+3)
14.如图,在3×3的正方形网格中有四个格点A,B,C,D,若以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是 ( )
A.点A B.点B C.点C D.点D
15.已知点A(2,3),其关于x轴的对称点是点B,点B关于y轴的对称点是点C,那么相当于将点A ( )
A.先向上平移6个单位长度,再向左平移4个单位长度后得到点C
B.先向下平移6个单位长度,再向左平移4个单位长度后得到点C
C.先向上平移6个单位长度,再向右平移4个单位长度后得到点C
D.先向下平移6个单位长度,再向右平移4个单位长度后得到点C
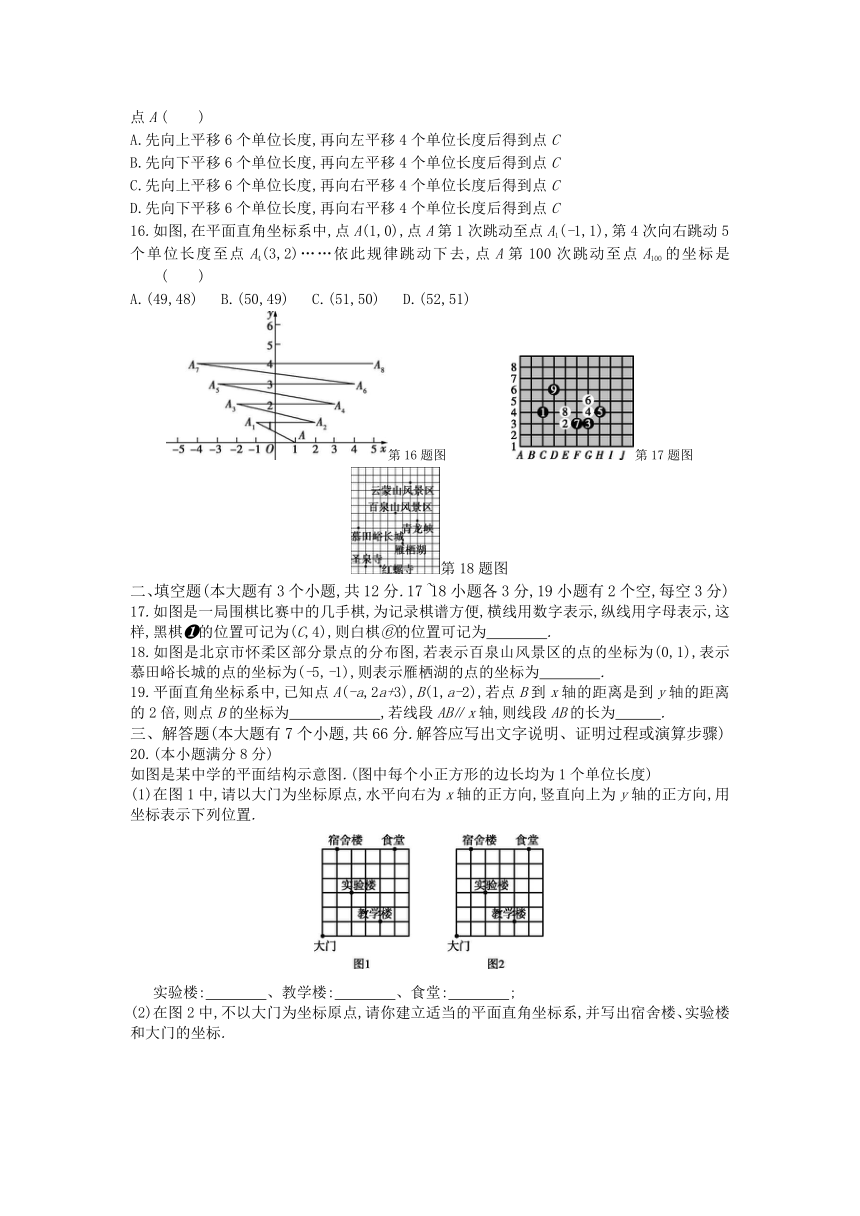
16.如图,在平面直角坐标系中,点A(1,0),点A第1次跳动至点A1(-1,1),第4次向右跳动5个单位长度至点A4(3,2)……依此规律跳动下去,点A第100次跳动至点A100的坐标是 ( )
A.(49,48) B.(50,49) C.(51,50) D.(52,51)
第16题图 第17题图 第18题图
二、填空题(本大题有3个小题,共12分.17~18小题各3分,19小题有2个空,每空3分)
17.如图是一局围棋比赛中的几手棋,为记录棋谱方便,横线用数字表示,纵线用字母表示,这样,黑棋?的位置可记为(C,4),则白棋⑥的位置可记为 .?
18.如图是北京市怀柔区部分景点的分布图,若表示百泉山风景区的点的坐标为(0,1),表示慕田峪长城的点的坐标为(-5,-1),则表示雁栖湖的点的坐标为 .?
19.平面直角坐标系中,已知点A(-a,2a+3),B(1,a-2),若点B到x轴的距离是到y轴的距离的2倍,则点B的坐标为 ,若线段AB∥x轴,则线段AB的长为 .?
三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)
如图是某中学的平面结构示意图.(图中每个小正方形的边长均为1个单位长度)
(1)在图1中,请以大门为坐标原点,水平向右为x轴的正方向,竖直向上为y轴的正方向,用坐标表示下列位置.
实验楼: 、教学楼: 、食堂: ;?
(2)在图2中,不以大门为坐标原点,请你建立适当的平面直角坐标系,并写出宿舍楼、实验楼和大门的坐标.
21.(本小题满分9分)
嘉琪的爸爸是个工程师,专门搞机械零件研究,几年前他开了家机械制造厂,自己设计,自己加工生产.有一天,他急需一个如图所示的配件,而这种配件又不能自己生产,附近厂家也没有能力生产,只有远在千里之外的一家大型工厂才能铸造生产.他在电话里努力地描述该配件的形状和大小,可对方一点儿也没弄明白,这可急坏了他.嘉琪知道了此事,接过电话,很快将这个零件的形状和尺寸告诉了对方,你认为嘉琪是用的什么方法?并简述说明.
22.(本小题满分9分)在平面直角坐标系中,已知点A,B都是x轴上的点,若点A的坐标为(4,0),且AB=5,点C的坐标为(2,5).
(1)请写出点B的坐标,并在如图所示的平面直角坐标系中画出符合条件的△ABC;
(2)求S△ABC.
23.(本小题满分9分)
已知点M(3a-8,a-1),根据下列条件分别求出点M的坐标.
(1)点M在x轴上;
(2)点M在第二、四象限的角平分线上;
(3)点M在第二象限,且a为整数;
(4)点N的坐标为(1,6),并且直线MN∥y轴.
24.(本小题满分10分)
△ABC的顶点在如图所示的正方形网格的格点(网格线的交点)上,每个小正方形的边长均为1.
(1)直接写出△ABC各顶点的坐标;
(2)画出△ABC关于x轴对称的图形△A1B1C1,并写出点B1的坐标;
(3)将△ABC先向右平移5个单位长度,再向上平移3个单位长度,画出平移后的图形△A2B2C2,并写出点C2的坐标.
25.(本小题满分10分)
如图,长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(4,0),点C的坐标为(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线匀速移动(即沿着长方形OABC移动一周).
(1)写出点B的坐标;
(2)当点P移动了4秒时,描出此时点P的位置,并写出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
26.(本小题满分11分)
平面直角坐标系中,点A(x,y),点A'(x',y'),当x'=x+m,y'=y+n,即点A'(x+m,y+n)时,表示点A到点A'的一个平移.例如:点A(x,y),点A'(x',y'),当x'=x+1,y'=y-2时,表示点A向右平移1个单位长度,再向下平移2个单位长度得到点A'.
根据上述定义,探究下列问题:
(1)已知点A(x,y),A'(x-3,y),则线段AA'的长度是多少;
(2)已知点A(x,y),A'(x+2,y-1),则线段AA'的长度是多少;
(3)长方形AOCB在平面直角坐标系中的位置如图所示,A(0,2),C(4,0),点A'(x',y'),若x'=x+m,y'=y-2m(m均为正数),点A'(x',y')能否在△OCB的直角边上?若能,求m的值;若不能,请说明理由.
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
D
A
B
A
D
D
B
C
A
B
D
C
C
B
B
C
17.(G,5) 18.(1,-3) 19.(1,2)或(1,-2) 4
20. (1)(2,3) (4,1) (5,6)
以大门为坐标原点,水平向右为x轴的正方向,竖直向上为y轴的正方向,建立如图1所示的平面直角坐标系.
则实验楼的坐标为(2,3)、教学楼的坐标为(4,1)、食堂的坐标为(5,6).
(2)以实验楼为坐标原点,水平向右为x轴的正方向,竖直向上为y轴的正方向,建立如图2所示的平面直角坐标系.
则宿舍楼的坐标为(-1,3)、实验楼的坐标为(0,0)、大门的坐标为(-2,-3).(答案不唯一,合理即可)
21. 嘉琪利用平面直角坐标系中点的坐标确定了该配件的形状和大小,方法如下:
(1)以配件的左下角顶点为原点,配件底边所在直线为x轴,最左边所在的直线为y轴,建立平面直角坐标系,如图所示.
(2)按照图示,在配件的各顶点处标注字母O,A,B,C,D,E,F,G,H,I,J,K,各点的坐标是O(0,0),A(4,0),B(4,2),C(6,2),D(6,0),E(8,0),F(8,5),G(4,7),H(4,3),I(2,3),J(2,8),K(0,8).
(3)告诉对方:以1 cm为单位长度建立平面直角坐标系,在直角坐标系中依次描出O,A,B,C,D,E,F,G,H,I,J,K各点,并顺次连接各点,则得到配件的形状和大小.
22. (1)由题意可知,点B的位置有两个:①当点B在点A的左边时,根据AB=5,得点B的坐标为(-1,0);②当点B在点A的右边时,根据AB=5,得点B的坐标为(9,0).
画图如图所示.
(2)因为点C的坐标为(2,5),所以点C到AB的距离为5,
所以S△ABC=×AB×5=×5×5=.
23. (1)∵点M在x轴上,
∴a-1=0,∴a=1,
∴3a-8=-5,
∴点M的坐标为(-5,0).
(2)∵点M在第二、四象限的角平分线上,
∴3a-8+a-1=0,
解得a=,
∴3a-8=3×-8=-,a-1=-1=,
∴点M的坐标为(-,).
(3)∵点M在第二象限,
∴
解得1又∵a为整数,∴a=2,
∴3a-8=-2,a-1=1,
∴点M的坐标为(-2,1).
(4)∵直线MN∥y轴,
∴3a-8=1,且a-1≠6,解得a=3,
∴a-1=2,
∴点M的坐标为(1,2).
24. (1)A(-2,0),B(-4,-3),C(-1,-4).
(2)画出的△A1B1C1如图所示.
由图可知点B1的坐标为(-4,3).
(3)画出的△A2B2C2如图所示.
由图可知点C2的坐标为(4,-1).
25. (1)∵点A的坐标为(4,0),点C的坐标为(0,6),
∴OA=4,OC=6,
又∵点B在第一象限内,
∴点B的坐标为(4,6).
(2)如图,∵点P移动了4秒时的路程是2×4=8,
∴此时点P为BC的中点,
∴点P的坐标为(2,6).
(3)∵点P到x轴的距离为5个单位长度,∴点P的纵坐标为5,
若点P在OC上,则OP=5,
5÷2=2.5(秒);
若点P在AB上,
则OC+BC+BP=6+4+(6-5)=11,
11÷2=5.5(秒).
综上,点P移动的时间为2.5秒或5.5秒.
26. (1)已知点A(x,y),A'(x-3,y),则线段AA'的长度是3.
(2)已知点A(x,y),A'(x+2,y-1),则线段AA'的长度是=.
(3)点A'(x',y')能在△OCB的直角边上.理由如下:
因为A(0,2),A'(x',y'),所以x'=x+m=m,y'=y-2m=2-2m.所以点A'的坐标为(m,2-2m).
若点A'在边OC上,则2-2m=0,解得m=1,此时点A'的坐标为(1,0).
因为C(4,0),所以当m=1时,点A'在边OC上.
若点A'在边BC上,则m=4,此时点A'的坐标为(4,-6),在第四象限,
所以当m=4时,点A'不在边BC上.
综上,当m=1时,点A'(x',y')在△OCB的直角边上.
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.以下描述中,能确定具体位置的是 ( )
A.万达电影院2排 B.距唐山高铁站2 km
C.北偏东30° D.东经106°,北纬31°
2.如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为 ( )
A.(2,2) B.(2,3)
C.(3,2) D.(0,3)
3.已知古塔在嘉淇的北偏东30°方向,且距离嘉淇2 km,符合条件的示意图是 ( )
4.下列各点中,通过上下平移不能与点(2,-1)重合的是 ( )
A.(-2,-1) B.(2,-2) C.(2,0) D.(2,-3)
5.已知点A(1,2)与点B(-1,a)关于原点对称,则a的值为 ( )
A.1 B.2 C.-1 D.-2
6.若点P(a,b)在第三象限,则点M(-a+2,b-3)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知平面直角坐标系中,长方形ABCD上各点的横坐标不变,纵坐标分别乘,则所得图形相当于将原图形 ( )
A.横向压缩为原来的 B.纵向压缩为原来的
C.横向拉长为原来的2倍 D.纵向压缩为原来的2倍
8.已知平面直角坐标系中点A的坐标为(-4,3),则下列结论正确的是 ( )
A.点A到x轴的距离为4
B.点A到y轴的距离为3
C.点A到原点的距离为5
D.点A关于x轴对称的点的坐标为(4,-3)
9.已知△ABC在平面直角坐标系中的位置如图所示,若△A'B'C'与△ABC关于y轴对称,则点A的对应点A'的坐标是 ( )
A.(3,2) B.(3,-2)
C.(2,3) D.(2,-3)
10.将点P(2m+3,m-2)向上平移1个单位长度后得到点P',且点P'在x轴上,那么点P的坐标是 ( )
A.(9,1) B.(5,-1) C.(7,0) D.(1,-3)
11.平面直角坐标系中的四边形ABCD,各顶点的横、纵坐标均扩大为原来的2倍,则下列说法正确的是 ( )
A.四边形ABCD的形状改变,面积变为原来的2倍
B.四边形ABCD的形状不变,面积变为原来的2倍
C.四边形ABCD的形状改变,面积变为原来的4倍
D.四边形ABCD的形状不变,面积变为原来的4倍
12.如图是A,B,C,D四位同学的家所在的位置,若以A同学家的位置为坐标原点建立平面直角坐标系,且C同学家的位置的坐标为(1,5),则B,D同学家的坐标分别为 ( )
A.(2,3),(3,2) B.(3,2),(2,3)
C.(3,2),(-2,3) D.(2,3),(-3,2)
第12题图 第13题图 第14题图
13.已知图1中的△ABC经过一定的变换后得到图2中的△A'B'C',如果图1中△ABC上的点P的坐标为(a,b),那么点P在图2中的对应点P'的坐标为 ( )
A.(a-2,b-3) B.(a-3,b-2) C.(a+3,b+2) D.(a+2,b+3)
14.如图,在3×3的正方形网格中有四个格点A,B,C,D,若以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是 ( )
A.点A B.点B C.点C D.点D
15.已知点A(2,3),其关于x轴的对称点是点B,点B关于y轴的对称点是点C,那么相当于将点A ( )
A.先向上平移6个单位长度,再向左平移4个单位长度后得到点C
B.先向下平移6个单位长度,再向左平移4个单位长度后得到点C
C.先向上平移6个单位长度,再向右平移4个单位长度后得到点C
D.先向下平移6个单位长度,再向右平移4个单位长度后得到点C
16.如图,在平面直角坐标系中,点A(1,0),点A第1次跳动至点A1(-1,1),第4次向右跳动5个单位长度至点A4(3,2)……依此规律跳动下去,点A第100次跳动至点A100的坐标是 ( )
A.(49,48) B.(50,49) C.(51,50) D.(52,51)
第16题图 第17题图 第18题图
二、填空题(本大题有3个小题,共12分.17~18小题各3分,19小题有2个空,每空3分)
17.如图是一局围棋比赛中的几手棋,为记录棋谱方便,横线用数字表示,纵线用字母表示,这样,黑棋?的位置可记为(C,4),则白棋⑥的位置可记为 .?
18.如图是北京市怀柔区部分景点的分布图,若表示百泉山风景区的点的坐标为(0,1),表示慕田峪长城的点的坐标为(-5,-1),则表示雁栖湖的点的坐标为 .?
19.平面直角坐标系中,已知点A(-a,2a+3),B(1,a-2),若点B到x轴的距离是到y轴的距离的2倍,则点B的坐标为 ,若线段AB∥x轴,则线段AB的长为 .?
三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)
如图是某中学的平面结构示意图.(图中每个小正方形的边长均为1个单位长度)
(1)在图1中,请以大门为坐标原点,水平向右为x轴的正方向,竖直向上为y轴的正方向,用坐标表示下列位置.
实验楼: 、教学楼: 、食堂: ;?
(2)在图2中,不以大门为坐标原点,请你建立适当的平面直角坐标系,并写出宿舍楼、实验楼和大门的坐标.
21.(本小题满分9分)
嘉琪的爸爸是个工程师,专门搞机械零件研究,几年前他开了家机械制造厂,自己设计,自己加工生产.有一天,他急需一个如图所示的配件,而这种配件又不能自己生产,附近厂家也没有能力生产,只有远在千里之外的一家大型工厂才能铸造生产.他在电话里努力地描述该配件的形状和大小,可对方一点儿也没弄明白,这可急坏了他.嘉琪知道了此事,接过电话,很快将这个零件的形状和尺寸告诉了对方,你认为嘉琪是用的什么方法?并简述说明.
22.(本小题满分9分)在平面直角坐标系中,已知点A,B都是x轴上的点,若点A的坐标为(4,0),且AB=5,点C的坐标为(2,5).
(1)请写出点B的坐标,并在如图所示的平面直角坐标系中画出符合条件的△ABC;
(2)求S△ABC.
23.(本小题满分9分)
已知点M(3a-8,a-1),根据下列条件分别求出点M的坐标.
(1)点M在x轴上;
(2)点M在第二、四象限的角平分线上;
(3)点M在第二象限,且a为整数;
(4)点N的坐标为(1,6),并且直线MN∥y轴.
24.(本小题满分10分)
△ABC的顶点在如图所示的正方形网格的格点(网格线的交点)上,每个小正方形的边长均为1.
(1)直接写出△ABC各顶点的坐标;
(2)画出△ABC关于x轴对称的图形△A1B1C1,并写出点B1的坐标;
(3)将△ABC先向右平移5个单位长度,再向上平移3个单位长度,画出平移后的图形△A2B2C2,并写出点C2的坐标.
25.(本小题满分10分)
如图,长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(4,0),点C的坐标为(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线匀速移动(即沿着长方形OABC移动一周).
(1)写出点B的坐标;
(2)当点P移动了4秒时,描出此时点P的位置,并写出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
26.(本小题满分11分)
平面直角坐标系中,点A(x,y),点A'(x',y'),当x'=x+m,y'=y+n,即点A'(x+m,y+n)时,表示点A到点A'的一个平移.例如:点A(x,y),点A'(x',y'),当x'=x+1,y'=y-2时,表示点A向右平移1个单位长度,再向下平移2个单位长度得到点A'.
根据上述定义,探究下列问题:
(1)已知点A(x,y),A'(x-3,y),则线段AA'的长度是多少;
(2)已知点A(x,y),A'(x+2,y-1),则线段AA'的长度是多少;
(3)长方形AOCB在平面直角坐标系中的位置如图所示,A(0,2),C(4,0),点A'(x',y'),若x'=x+m,y'=y-2m(m均为正数),点A'(x',y')能否在△OCB的直角边上?若能,求m的值;若不能,请说明理由.
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
D
A
B
A
D
D
B
C
A
B
D
C
C
B
B
C
17.(G,5) 18.(1,-3) 19.(1,2)或(1,-2) 4
20. (1)(2,3) (4,1) (5,6)
以大门为坐标原点,水平向右为x轴的正方向,竖直向上为y轴的正方向,建立如图1所示的平面直角坐标系.
则实验楼的坐标为(2,3)、教学楼的坐标为(4,1)、食堂的坐标为(5,6).
(2)以实验楼为坐标原点,水平向右为x轴的正方向,竖直向上为y轴的正方向,建立如图2所示的平面直角坐标系.
则宿舍楼的坐标为(-1,3)、实验楼的坐标为(0,0)、大门的坐标为(-2,-3).(答案不唯一,合理即可)
21. 嘉琪利用平面直角坐标系中点的坐标确定了该配件的形状和大小,方法如下:
(1)以配件的左下角顶点为原点,配件底边所在直线为x轴,最左边所在的直线为y轴,建立平面直角坐标系,如图所示.
(2)按照图示,在配件的各顶点处标注字母O,A,B,C,D,E,F,G,H,I,J,K,各点的坐标是O(0,0),A(4,0),B(4,2),C(6,2),D(6,0),E(8,0),F(8,5),G(4,7),H(4,3),I(2,3),J(2,8),K(0,8).
(3)告诉对方:以1 cm为单位长度建立平面直角坐标系,在直角坐标系中依次描出O,A,B,C,D,E,F,G,H,I,J,K各点,并顺次连接各点,则得到配件的形状和大小.
22. (1)由题意可知,点B的位置有两个:①当点B在点A的左边时,根据AB=5,得点B的坐标为(-1,0);②当点B在点A的右边时,根据AB=5,得点B的坐标为(9,0).
画图如图所示.
(2)因为点C的坐标为(2,5),所以点C到AB的距离为5,
所以S△ABC=×AB×5=×5×5=.
23. (1)∵点M在x轴上,
∴a-1=0,∴a=1,
∴3a-8=-5,
∴点M的坐标为(-5,0).
(2)∵点M在第二、四象限的角平分线上,
∴3a-8+a-1=0,
解得a=,
∴3a-8=3×-8=-,a-1=-1=,
∴点M的坐标为(-,).
(3)∵点M在第二象限,
∴
解得1
∴3a-8=-2,a-1=1,
∴点M的坐标为(-2,1).
(4)∵直线MN∥y轴,
∴3a-8=1,且a-1≠6,解得a=3,
∴a-1=2,
∴点M的坐标为(1,2).
24. (1)A(-2,0),B(-4,-3),C(-1,-4).
(2)画出的△A1B1C1如图所示.
由图可知点B1的坐标为(-4,3).
(3)画出的△A2B2C2如图所示.
由图可知点C2的坐标为(4,-1).
25. (1)∵点A的坐标为(4,0),点C的坐标为(0,6),
∴OA=4,OC=6,
又∵点B在第一象限内,
∴点B的坐标为(4,6).
(2)如图,∵点P移动了4秒时的路程是2×4=8,
∴此时点P为BC的中点,
∴点P的坐标为(2,6).
(3)∵点P到x轴的距离为5个单位长度,∴点P的纵坐标为5,
若点P在OC上,则OP=5,
5÷2=2.5(秒);
若点P在AB上,
则OC+BC+BP=6+4+(6-5)=11,
11÷2=5.5(秒).
综上,点P移动的时间为2.5秒或5.5秒.
26. (1)已知点A(x,y),A'(x-3,y),则线段AA'的长度是3.
(2)已知点A(x,y),A'(x+2,y-1),则线段AA'的长度是=.
(3)点A'(x',y')能在△OCB的直角边上.理由如下:
因为A(0,2),A'(x',y'),所以x'=x+m=m,y'=y-2m=2-2m.所以点A'的坐标为(m,2-2m).
若点A'在边OC上,则2-2m=0,解得m=1,此时点A'的坐标为(1,0).
因为C(4,0),所以当m=1时,点A'在边OC上.
若点A'在边BC上,则m=4,此时点A'的坐标为(4,-6),在第四象限,
所以当m=4时,点A'不在边BC上.
综上,当m=1时,点A'(x',y')在△OCB的直角边上.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
