冀教版初中数学七年级下册 第七章 相交线与平行线习 平行线习 题课 教案
文档属性
| 名称 | 冀教版初中数学七年级下册 第七章 相交线与平行线习 平行线习 题课 教案 | 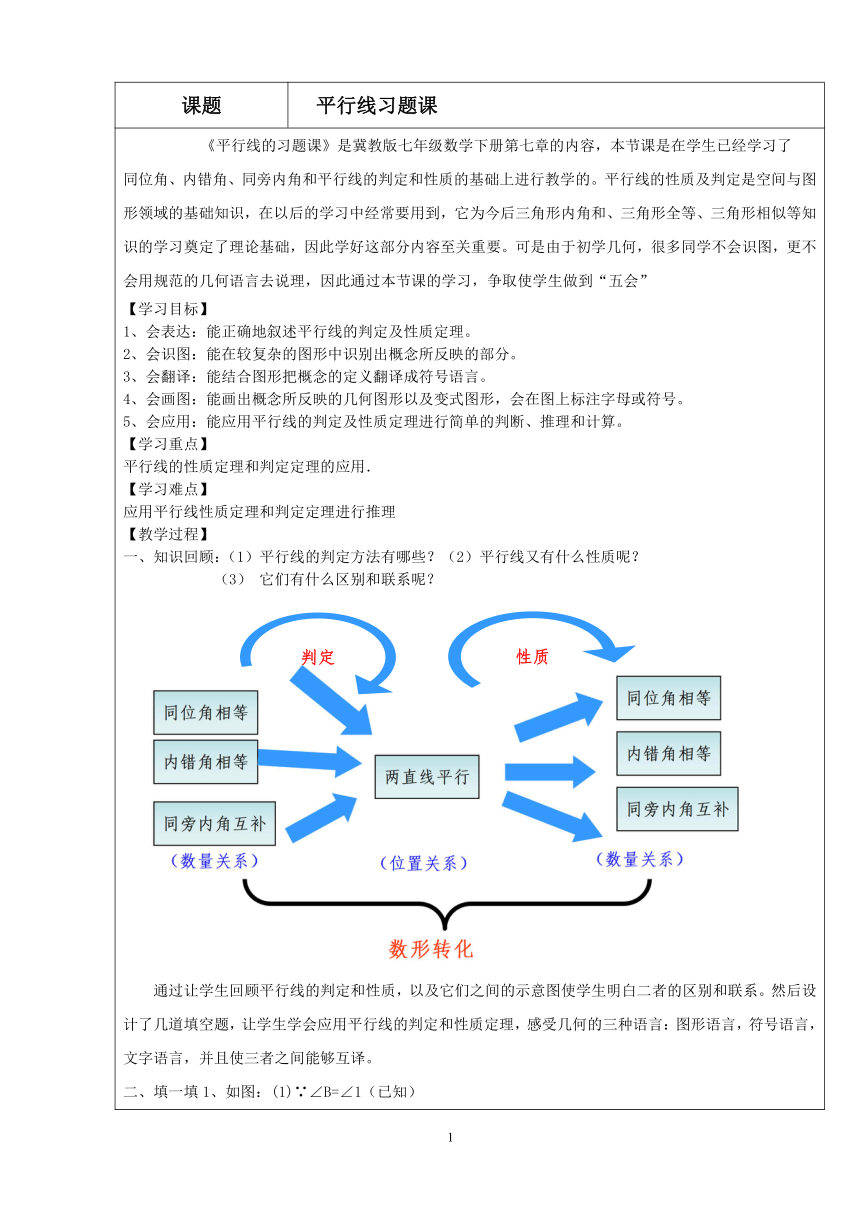 | |
| 格式 | doc | ||
| 文件大小 | 118.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 13:33:57 | ||
图片预览


文档简介
课题
平行线习题课
《平行线的习题课》是冀教版七年级数学下册第七章的内容,本节课是在学生已经学习了
同位角、内错角、同旁内角和平行线的判定和性质的基础上进行教学的。平行线的性质及判定是空间与图形领域的基础知识,在以后的学习中经常要用到,它为今后三角形内角和、三角形全等、三角形相似等知识的学习奠定了理论基础,因此学好这部分内容至关重要。可是由于初学几何,很多同学不会识图,更不会用规范的几何语言去说理,因此通过本节课的学习,争取使学生做到“五会”
【学习目标】
1、会表达:能正确地叙述平行线的判定及性质定理。
2、会识图:能在较复杂的图形中识别出概念所反映的部分。
3、会翻译:能结合图形把概念的定义翻译成符号语言。
4、会画图:能画出概念所反映的几何图形以及变式图形,会在图上标注字母或符号。
5、会应用:能应用平行线的判定及性质定理进行简单的判断、推理和计算。
【学习重点】
平行线的性质定理和判定定理的应用.
【学习难点】
应用平行线性质定理和判定定理进行推理
【教学过程】
知识回顾:(1)平行线的判定方法有哪些?(2)平行线又有什么性质呢?
(3) 它们有什么区别和联系呢?
2860040185420性质
性质
1029970195580判定
判定
数形转化
(数量关系)
(位置关系)
(数量关系)
内错角相等
同旁内角互补
同位角相等
两直线平行
同旁内角互补
同位角相等
内错角相等
数形转化
(数量关系)
(位置关系)
(数量关系)
内错角相等
同旁内角互补
同位角相等
两直线平行
同旁内角互补
同位角相等
内错角相等
通过让学生回顾平行线的判定和性质,以及它们之间的示意图使学生明白二者的区别和联系。然后设计了几道填空题,让学生学会应用平行线的判定和性质定理,感受几何的三种语言:图形语言,符号语言,文字语言,并且使三者之间能够互译。
二、填一填1、如图:(1)∵∠B=∠1(已知)
∴____//____( )
(2)∵∠3=∠D(已知)
G
5
4
3
F
E
D
C
B
A
2
1
∴____//____( )
(3)∵∠B+∠4=180°(已知)
∴____//____( )
(4)∵CG // DF(已知)
∴∠2=_____ ( )
(5) ∵AB // DE(已知)
∴∠3=_____ ( )
(6)∵CG // DF(已知)
∴∠F+ =180°( )
然后由浅入深设计了一道说理题,使学生明白在解题时要学会把复杂图形分解为基本图形 ;在尝试说理时,对于过程的书写要讲究逻辑,先因后果,因果对应,推理严密,言必有据。
38862001917704
3
2
1
4
3
2
1
能力挑战
三、202882586360尝试推理: C D C D
2、如图,AB∥CD
让学生猜想
F E
问题:(1)可得什么结论? A B
A B
(1) (2)
(2)若∠1= ∠2,又可得什么结论? (学生思考后回答,师板书推理过程)
①∠3= ∠4 ⑵ DF ∥ AE
(3)出示问题:如图,AB∥CD,∠1=∠2,试说明 DF ∥ AE
3429000927104
3
2
1
4
3
2
1
(4)连结EF,请问又能得出什么结论? C D
(5)出示问题: 如图,AB∥CD,∠1=∠2 F E
∠E=37°,求:∠F
(学生在练习本上完成推理,代表展示)
A B
最后提高难度,对一道习题尝试说理,并通过变式尝试书写推理过程,体验成功喜悦;
3、尝试说理(1) 已知:CD∥EF, ∠1= ∠2,
试说明: ∠AGD= ∠ACB(师分析,让学生学会由已知看可知,由未知想需知, 学生交流后有代表回答,师板书)
变式:(2)已知: CD∥EF, ∠AGD= ∠ACB. B
2
3
1
E
F
G
D
C
A
B
2
3
1
E
F
G
D
C
A
试说明: ∠1= ∠2
(3)已知:∠AGD= ∠ACB,∠1= ∠2.
试说明: CD∥EF.(两道变式题由学生独立思考,合作交流,尝试书写推理过程,代表展示)
四、课堂小结:
解决几何问题的方法
(1)分析问题的方法:
由已知看可知,扩大已知面。
由未知想需知,明确解题方向
(2)识图的方法:
会在定理图形中提炼基本图形,
会在解题时把复杂图形分解为基本图形
结束寄语:
严格性之于数学,犹如道德之于人.
3430270-4445E
E
由“因”导“果”,言必有据.是初学
297180092710365887094615证明者谨记和遵循的原则.
37719001917701
1
六、布置作业:
3430270-44453
3
537210092710C
C
297307094615D
D
1:已知:如图∠1= ∠ 2, ∠ A= ∠ C,
331470092710491490092710 说明:AE∥BC
2971800290830A 2 B
通过应用定理进行简单的推理,锻炼学生的观察能力、动手能力和思维能力,提高学生的分析、识图、逻辑推理以及语言表达能力,增强学习数学的兴趣;使他们能够主动探索与合作交流,领会数形结合、转化的数学思想和方法,调动了学生学习的积极性;让学生在轻松的学习气氛中去发现问题,激发学生的求知欲;这样不但解决了本节课的重点与难点,让每个学生都能从同伴的交流中获益,同时也培养了学生的合作意识,提高了学生的动手、动口能力和归纳能力。让学生在愤悱中学习,在学习中合作,在合作中交流,在交流中学会。
平行线习题课
《平行线的习题课》是冀教版七年级数学下册第七章的内容,本节课是在学生已经学习了
同位角、内错角、同旁内角和平行线的判定和性质的基础上进行教学的。平行线的性质及判定是空间与图形领域的基础知识,在以后的学习中经常要用到,它为今后三角形内角和、三角形全等、三角形相似等知识的学习奠定了理论基础,因此学好这部分内容至关重要。可是由于初学几何,很多同学不会识图,更不会用规范的几何语言去说理,因此通过本节课的学习,争取使学生做到“五会”
【学习目标】
1、会表达:能正确地叙述平行线的判定及性质定理。
2、会识图:能在较复杂的图形中识别出概念所反映的部分。
3、会翻译:能结合图形把概念的定义翻译成符号语言。
4、会画图:能画出概念所反映的几何图形以及变式图形,会在图上标注字母或符号。
5、会应用:能应用平行线的判定及性质定理进行简单的判断、推理和计算。
【学习重点】
平行线的性质定理和判定定理的应用.
【学习难点】
应用平行线性质定理和判定定理进行推理
【教学过程】
知识回顾:(1)平行线的判定方法有哪些?(2)平行线又有什么性质呢?
(3) 它们有什么区别和联系呢?
2860040185420性质
性质
1029970195580判定
判定
数形转化
(数量关系)
(位置关系)
(数量关系)
内错角相等
同旁内角互补
同位角相等
两直线平行
同旁内角互补
同位角相等
内错角相等
数形转化
(数量关系)
(位置关系)
(数量关系)
内错角相等
同旁内角互补
同位角相等
两直线平行
同旁内角互补
同位角相等
内错角相等
通过让学生回顾平行线的判定和性质,以及它们之间的示意图使学生明白二者的区别和联系。然后设计了几道填空题,让学生学会应用平行线的判定和性质定理,感受几何的三种语言:图形语言,符号语言,文字语言,并且使三者之间能够互译。
二、填一填1、如图:(1)∵∠B=∠1(已知)
∴____//____( )
(2)∵∠3=∠D(已知)
G
5
4
3
F
E
D
C
B
A
2
1
∴____//____( )
(3)∵∠B+∠4=180°(已知)
∴____//____( )
(4)∵CG // DF(已知)
∴∠2=_____ ( )
(5) ∵AB // DE(已知)
∴∠3=_____ ( )
(6)∵CG // DF(已知)
∴∠F+ =180°( )
然后由浅入深设计了一道说理题,使学生明白在解题时要学会把复杂图形分解为基本图形 ;在尝试说理时,对于过程的书写要讲究逻辑,先因后果,因果对应,推理严密,言必有据。
38862001917704
3
2
1
4
3
2
1
能力挑战
三、202882586360尝试推理: C D C D
2、如图,AB∥CD
让学生猜想
F E
问题:(1)可得什么结论? A B
A B
(1) (2)
(2)若∠1= ∠2,又可得什么结论? (学生思考后回答,师板书推理过程)
①∠3= ∠4 ⑵ DF ∥ AE
(3)出示问题:如图,AB∥CD,∠1=∠2,试说明 DF ∥ AE
3429000927104
3
2
1
4
3
2
1
(4)连结EF,请问又能得出什么结论? C D
(5)出示问题: 如图,AB∥CD,∠1=∠2 F E
∠E=37°,求:∠F
(学生在练习本上完成推理,代表展示)
A B
最后提高难度,对一道习题尝试说理,并通过变式尝试书写推理过程,体验成功喜悦;
3、尝试说理(1) 已知:CD∥EF, ∠1= ∠2,
试说明: ∠AGD= ∠ACB(师分析,让学生学会由已知看可知,由未知想需知, 学生交流后有代表回答,师板书)
变式:(2)已知: CD∥EF, ∠AGD= ∠ACB. B
2
3
1
E
F
G
D
C
A
B
2
3
1
E
F
G
D
C
A
试说明: ∠1= ∠2
(3)已知:∠AGD= ∠ACB,∠1= ∠2.
试说明: CD∥EF.(两道变式题由学生独立思考,合作交流,尝试书写推理过程,代表展示)
四、课堂小结:
解决几何问题的方法
(1)分析问题的方法:
由已知看可知,扩大已知面。
由未知想需知,明确解题方向
(2)识图的方法:
会在定理图形中提炼基本图形,
会在解题时把复杂图形分解为基本图形
结束寄语:
严格性之于数学,犹如道德之于人.
3430270-4445E
E
由“因”导“果”,言必有据.是初学
297180092710365887094615证明者谨记和遵循的原则.
37719001917701
1
六、布置作业:
3430270-44453
3
537210092710C
C
297307094615D
D
1:已知:如图∠1= ∠ 2, ∠ A= ∠ C,
331470092710491490092710 说明:AE∥BC
2971800290830A 2 B
通过应用定理进行简单的推理,锻炼学生的观察能力、动手能力和思维能力,提高学生的分析、识图、逻辑推理以及语言表达能力,增强学习数学的兴趣;使他们能够主动探索与合作交流,领会数形结合、转化的数学思想和方法,调动了学生学习的积极性;让学生在轻松的学习气氛中去发现问题,激发学生的求知欲;这样不但解决了本节课的重点与难点,让每个学生都能从同伴的交流中获益,同时也培养了学生的合作意识,提高了学生的动手、动口能力和归纳能力。让学生在愤悱中学习,在学习中合作,在合作中交流,在交流中学会。
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
