第四章《图形的认识》达标检测题（含解析）

中小学教育资源及组卷应用平台
湘教版七年级数学上册
第四章达标检测题
(本试卷分第Ⅰ卷和第Ⅱ卷，考试时间：120分钟，赋分：120分)
第Ⅰ卷　(选择题　共36分)
选择题(本大题共12小题，每小题3分，共36分)
1．(白银中考)下列四个几何体中，是三棱柱的为(　　)
A
B
C
D
2．小张同学的座右铭是“态度决定一切”，他将这几个字写在一个正方体纸盒的每个面上，其平面展开图如图所示，那么在该正方体中，和“一”相对的字是(　　)
A.态
B．度
C．决
D．切
3．下列四个生活、生产现象：
①用两个钉子就可以把木条固定在墙上；
②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；
③从A地到B地架设电线，总是尽可能沿着线段AB架设；
④把弯曲的公路改直，就能缩短路程．
其中可用公理“两点之间，线段最短”来解释的现象是(　　)
A．①②
B．①③
C．②④
D．③④
4．下列各图中的几何图形能相交的是(　　)
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
5．下列语句：
①一条直线有且只有一条垂线；②不相等的两个角一定不是对顶角；③不在同一直线上的四个点可以画6条直线；④如果两个角是邻补角，那么这两个角的平分线所成的角是直角．
其中错误的有(　　)
A．1个
B．2个
C．3个
D．4个
6．★如果线段AB＝6
cm，BC＝4
cm，且线段A，B，C在同一直线上，那么A，C两点之间的距离是(　　)
A．10
cm
B．2
cm
C．10
cm或2
cm
D．无法确定
7．如图，已知A，B，C，D，E五点在同一直线上，点D是线段AB的中点，点E是线段BC的中点，若线段AC＝12，则线段DE等于(　　)
A．10
B．8
C．6
D．4
8．点A，B，C在同一条数轴上，其中点A，B表示的数分别为－3，1，若BC＝2，则AC等于(　　)
A．3
B．2
C．3或5
D．2或6
9．在∠AOB的内部任取一点C，作射线OC，则一定存在(　　)
A．∠AOB＞∠AOC
B．∠AOB＜∠BOC
C．∠BOC＞∠AOC
D．∠AOC＞∠BOC
10．如果一个角的余角是50°，那么这个角的补角的度数是(　　)
A．130°
B．40°
C．90°
D．140°
11．将一副直角三角尺如图放置，若∠AOD＝20°，则∠BOC的大小为(　　)
A.140°
B．160°
C．170°
D．150°
12．★如图，OB是∠AOC的平分线，OD是∠COE的平分线，若∠AOB＝40°，∠COE＝60°，则∠BOD的度数为(　　)
A．50°
B．60°
C．65°
D．70°
eq
\o(\s\up7(),\s\do5(第12题图))
　　　
eq
\o(\s\up7(),\s\do5(第13题图))
第Ⅱ卷　(非选择题　共84分)
二、填空题(本大题共6小题，每小题3分，共18分)
13．如图是某个几何体的表面展开图，那么这个几何体是
．
14．如图，点A，B，C在直线l上，则图中共有
条线段，有
条射线．
15．A，B，C三点在同一条直线上，若BC＝2AB且AB＝m，则AC＝
．
16．如图，点O是直线AD上的点，∠AOB，∠BOC，∠COD三个角从小到大依次相差25°，则这三个角中最小角的度数是
．
eq
\o(\s\up7(),\s\do5(第16题图))
　
eq
\o(\s\up7(),\s\do5(第17题图))
17．如图，把一张长方形纸片ABCD沿EF折叠，点C，D分别落在点C′，D′的位置上，EC′交AD于G，已知∠FEG＝56°，那么∠BEG＝
．
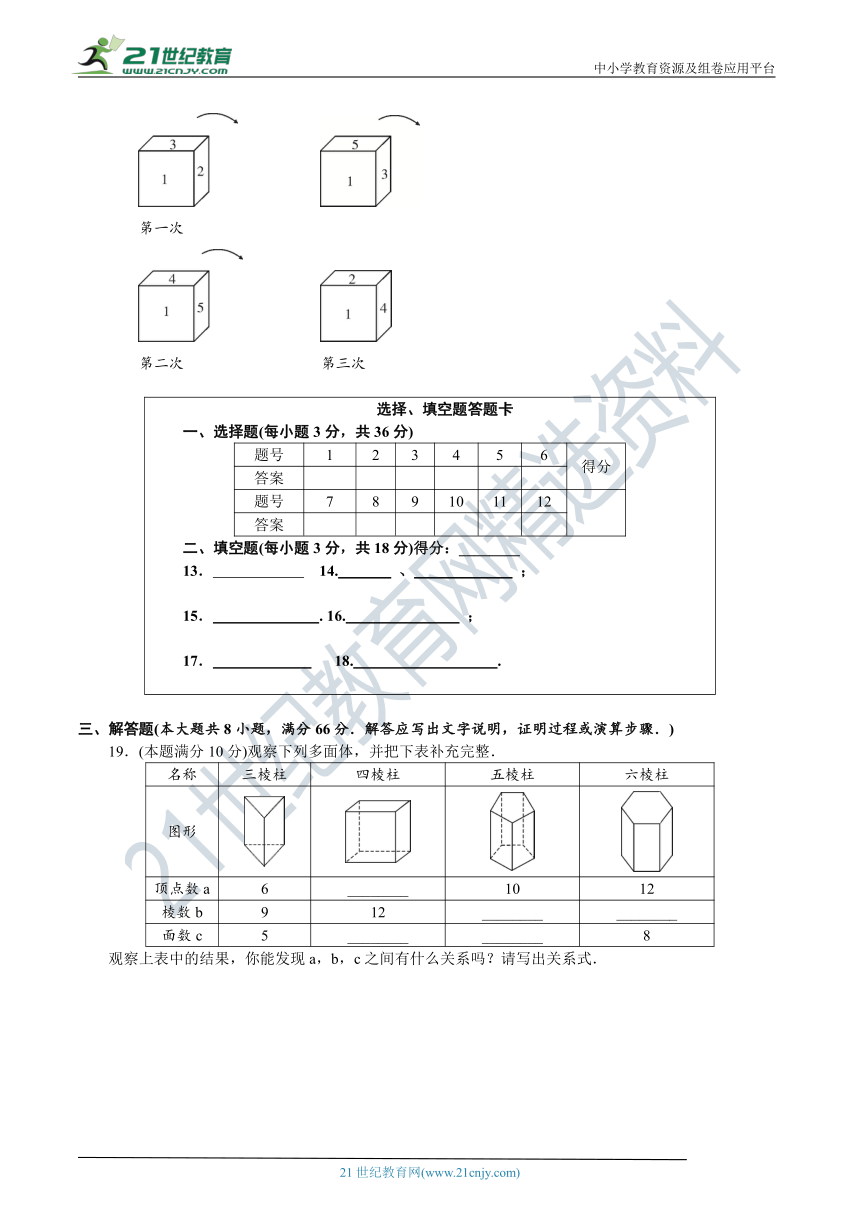
18．★有一个正六面体骰子放在桌面上，将骰子沿如图所示顺时针方向滚动，每滚动90°算一次，则滚动第2
020次后，骰子朝下一面的数字是
．
　　
第一次　　
第二次
第三次
选择、填空题答题卡一、选择题(每小题3分，共36分)题号123456得分答案题号789101112答案二、填空题(每小题3分，共18分)得分：________13．
　14.
、
；
15．
.
16.
；
17．
18.
.
三、解答题(本大题共8小题，满分66分．解答应写出文字说明，证明过程或演算步骤．)
19．(本题满分10分)观察下列多面体，并把下表补充完整．
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数a
6
________
10
12
棱数b
9
12
________
________
面数c
5
________
________
8
观察上表中的结果，你能发现a，b，c之间有什么关系吗？请写出关系式．
20．(本题满分5分)如图，C为线段AB上的一点，AC∶CB＝3∶2，D，E两点分别为AC，AB的中点，若线段DE为2
cm，则AB的长为多少？
21．(本题满分6分)如图，OD平分∠AOB，OE平分∠BOC，∠COD＝20°，∠AOB＝140°，求∠DOE的度数．
22．(本题满分8分)如图，线段AD＝6
cm，线段AC＝BD＝4
cm，E，F分别是线段AB，CD的中点，求线段EF的长．
23．(本题满分8分)观察下图，回答下列问题：
(1)在图①中角的个数有多少？
(2)在图②中角的个数有多少？
(3)在图③中角的个数有多少？
(4)依此类推，如图④所示，若一个角内有n条射线，此时共有多少个角？
eq
\o(\s\up7(),\s\do5(①))
　　　　
eq
\o(\s\up7(),\s\do5(②))
③
④
24．(本题满分8分)如图，直线AB，CD相交于点O，OE平分∠AOD，∠FOC＝90°，∠1＝40°，求∠2和∠3的度数．
25．(本题满分11分)(沙河口区期末)已知∠AOB＝α，过O作射线OC，OM平分∠AOC，ON平分∠BOC.
(1)如图，若α＝120°，当OC在∠AOB内部时，求∠MON的度数；
(2)当OC在∠AOB外部时，画出相应图形，求∠MON的度数(用含α的式子表示).
eq
\o(\s\up7(),\s\do5(题图))
26．(本题满分10分)(孝南区期末)如图，已知数轴上点A表示的数为a，点B表示的数为b，且满足(a－6)2＋|b＋4|＝0.
(1)写出a，b及AB的距离：
a＝________；b＝________；AB＝________；
(2)若动点P从点A出发，以每秒6个单位长度沿数轴向左匀速运动，动点Q从点B出发，以每秒4个单位长度向左匀速运动．
①若P，Q同时出发，问点P运动多少秒追上点Q?
②若M为AP的中点，N为PB的中点，点P在运动过程中，线段MN是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长．
参考答案
第Ⅰ卷　(选择题　共36分)
选择题(本大题共12小题，每小题3分，共36分)
1．(白银中考)下列四个几何体中，是三棱柱的为(　C　)
A
B
C
D
2．小张同学的座右铭是“态度决定一切”，他将这几个字写在一个正方体纸盒的每个面上，其平面展开图如图所示，那么在该正方体中，和“一”相对的字是(　A　)
A.态
B．度
C．决
D．切
3．下列四个生活、生产现象：
①用两个钉子就可以把木条固定在墙上；
②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；
③从A地到B地架设电线，总是尽可能沿着线段AB架设；
④把弯曲的公路改直，就能缩短路程．
其中可用公理“两点之间，线段最短”来解释的现象是(　D　)
A．①②
B．①③
C．②④
D．③④
4．下列各图中的几何图形能相交的是(　A　)
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
5．下列语句：
①一条直线有且只有一条垂线；②不相等的两个角一定不是对顶角；③不在同一直线上的四个点可以画6条直线；④如果两个角是邻补角，那么这两个角的平分线所成的角是直角．
其中错误的有(　B　)
A．1个
B．2个
C．3个
D．4个
6．★如果线段AB＝6
cm，BC＝4
cm，且线段A，B，C在同一直线上，那么A，C两点之间的距离是(　C　)
A．10
cm
B．2
cm
C．10
cm或2
cm
D．无法确定
7．如图，已知A，B，C，D，E五点在同一直线上，点D是线段AB的中点，点E是线段BC的中点，若线段AC＝12，则线段DE等于(　C　)
A．10
B．8
C．6
D．4
8．点A，B，C在同一条数轴上，其中点A，B表示的数分别为－3，1，若BC＝2，则AC等于(　D　)
A．3
B．2
C．3或5
D．2或6
9．在∠AOB的内部任取一点C，作射线OC，则一定存在(　A　)
A．∠AOB＞∠AOC
B．∠AOB＜∠BOC
C．∠BOC＞∠AOC
D．∠AOC＞∠BOC
10．如果一个角的余角是50°，那么这个角的补角的度数是(　D　)
A．130°
B．40°
C．90°
D．140°
11．将一副直角三角尺如图放置，若∠AOD＝20°，则∠BOC的大小为(　B　)
A.140°
B．160°
C．170°
D．150°
12．★如图，OB是∠AOC的平分线，OD是∠COE的平分线，若∠AOB＝40°，∠COE＝60°，则∠BOD的度数为(　D　)
A．50°
B．60°
C．65°
D．70°
eq
\o(\s\up7(),\s\do5(第12题图))
　　　
eq
\o(\s\up7(),\s\do5(第13题图))
第Ⅱ卷　(非选择题　共84分)
二、填空题(本大题共6小题，每小题3分，共18分)
13．如图是某个几何体的表面展开图，那么这个几何体是
圆锥
．
14．如图，点A，B，C在直线l上，则图中共有
3
条线段，有
6
条射线．
15．A，B，C三点在同一条直线上，若BC＝2AB且AB＝m，则AC＝
m或3m
．
16．如图，点O是直线AD上的点，∠AOB，∠BOC，∠COD三个角从小到大依次相差25°，则这三个角中最小角的度数是
35°
．
eq
\o(\s\up7(),\s\do5(第16题图))
　
eq
\o(\s\up7(),\s\do5(第17题图))
17．如图，把一张长方形纸片ABCD沿EF折叠，点C，D分别落在点C′，D′的位置上，EC′交AD于G，已知∠FEG＝56°，那么∠BEG＝
68°
．
18．★有一个正六面体骰子放在桌面上，将骰子沿如图所示顺时针方向滚动，每滚动90°算一次，则滚动第2
020次后，骰子朝下一面的数字是
4
．
　　
第一次　　
第二次
第三次
选择、填空题答题卡一、选择题(每小题3分，共36分)题号123456答案CADABC得分题号789101112答案CDADBD二、填空题(每小题3分，共18分)得分：________13．
圆锥
　
14.
3
　
6
　15.
m或3m
16．
35°
17.
68°
18.
4
三、解答题(本大题共8小题，满分66分．解答应写出文字说明，证明过程或演算步骤．)
19．(本题满分10分)观察下列多面体，并把下表补充完整．
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数a
6
________
10
12
棱数b
9
12
________
________
面数c
5
________
________
8
观察上表中的结果，你能发现a，b，c之间有什么关系吗？请写出关系式．
解：答案为：8，15，18，6，7；
关系式：a＋c－b＝2.
20．(本题满分5分)如图，C为线段AB上的一点，AC∶CB＝3∶2，D，E两点分别为AC，AB的中点，若线段DE为2
cm，则AB的长为多少？
解：设AB＝x，由题意得
AC＝x，BC＝x，
∵D，E两点分别为AC，AB的中点，
∴DC＝x，BE＝x，
DE＝DC－EC＝DC－(BE－BC)，
即x－＝2，
解得x＝10，
则AB的长为10
cm.
21．(本题满分6分)如图，OD平分∠AOB，OE平分∠BOC，∠COD＝20°，∠AOB＝140°，求∠DOE的度数．
解：∵OD平分∠AOB，∠AOB＝140°，
∴∠AOD＝∠AOB＝70°，
∴∠BOC＝∠AOB－∠AOD－∠COD＝50°，
∴∠COE＝∠BOC＝25°，
∴∠DOE＝∠COD＋∠COE＝45°.
22．(本题满分8分)如图，线段AD＝6
cm，线段AC＝BD＝4
cm，E，F分别是线段AB，CD的中点，求线段EF的长．
解：∵线段AD＝6
cm，线段AC＝BD＝4
cm，
∴BC＝AC＋BD－AD＝4＋4－6＝2(cm).
∴AB＋CD＝AD－BC＝6－2＝4(cm).
又∵E，F分别是线段AB，CD的中点，
∴EB＝AB，CF＝CD.
∴EB＋CF＝AB＋CD
＝(AB＋CD)
＝×4
＝2(cm).
∴EF＝EB＋BC＋CF＝2＋2＝4(cm).
答：线段EF的长为4
cm.
23．(本题满分8分)观察下图，回答下列问题：
(1)在图①中角的个数有多少？
(2)在图②中角的个数有多少？
(3)在图③中角的个数有多少？
(4)依此类推，如图④所示，若一个角内有n条射线，此时共有多少个角？
eq
\o(\s\up7(),\s\do5(①))
　　　　
eq
\o(\s\up7(),\s\do5(②))
③
④
解：由分析知：
(1)图①中有2条射线，则角的个数为＝1(个)；
(2)图②中有3条射线，则角的个数为＝3(个)；
(3)图③中有4条射线，则角的个数为＝6(个)；
(4)由(1)(2)(3)类推，角内有n条射线时，图中共有(n＋2)条射线，此时共有
个角．
24．(本题满分8分)如图，直线AB，CD相交于点O，OE平分∠AOD，∠FOC＝90°，∠1＝40°，求∠2和∠3的度数．
解：∵∠FOC＝90°，
∠1＝40°，AB为直线，
∴∠3＋∠FOC＋∠1
＝180°，
∴∠3＝180°－90°－40°
＝50°.
∵∠3与∠AOD互补，
∴∠AOD＝180°－∠3＝130°.
∵OE平分∠AOD，
∴∠2＝∠AOD＝65°.
25．(本题满分11分)(沙河口区期末)已知∠AOB＝α，过O作射线OC，OM平分∠AOC，ON平分∠BOC.
(1)如图，若α＝120°，当OC在∠AOB内部时，求∠MON的度数；
(2)当OC在∠AOB外部时，画出相应图形，求∠MON的度数(用含α的式子表示).
eq
\o(\s\up7(),\s\do5(题图))
解：(1)∵OM平分∠AOC，ON平分∠BOC，
∴∠MOC＝∠AOC，∠NOC＝∠BOC，
∴∠MON＝∠MOC＋∠NOC
＝∠AOC＋∠BOC
＝(∠AOC＋∠BOC)
＝∠AOB＝α
＝60°.
(2)如答图．
答图
∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝(∠AOB＋∠BOC)，
∠CON＝∠BOC.
∴∠MON＝∠MOC－∠CON
＝(∠AOB＋∠BOC)－∠BOC
＝∠AOB
＝α.
26．(本题满分10分)(孝南区期末)如图，已知数轴上点A表示的数为a，点B表示的数为b，且满足(a－6)2＋|b＋4|＝0.
(1)写出a，b及AB的距离：
a＝________；b＝________；AB＝________；
(2)若动点P从点A出发，以每秒6个单位长度沿数轴向左匀速运动，动点Q从点B出发，以每秒4个单位长度向左匀速运动．
①若P，Q同时出发，问点P运动多少秒追上点Q?
②若M为AP的中点，N为PB的中点，点P在运动过程中，线段MN是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长．
解：(1)∵(a－6)2＋|b＋4|＝0，
∴a－6＝0，b＋4＝0，
解得a＝6，b＝－4，
∴AB＝10，
故答案为6；－4；10.
(2)①设点P运动t秒时追上点Q，则
6t－4t＝10，
∴t＝5，
即点P运动5秒时追上点Q.
②线段MN不发生变化，
理由：
当P在线段AB之间时，如图①：
MN＝AB－(BN＋AM)
＝AB－
＝AB－(BP＋AP)
＝AB－AB＝5.
当P在线段AB的延长线上时，如图②：
MN＝AP－PB＝AB＝5，
故MN的长不发生变化．
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)