人教版数学八年级上册 第12章 12.2三角形全等的判定同步测试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 第12章 12.2三角形全等的判定同步测试题(一)(Word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览


文档简介
三角形全等的判定同步测试题(一)
一.选择题
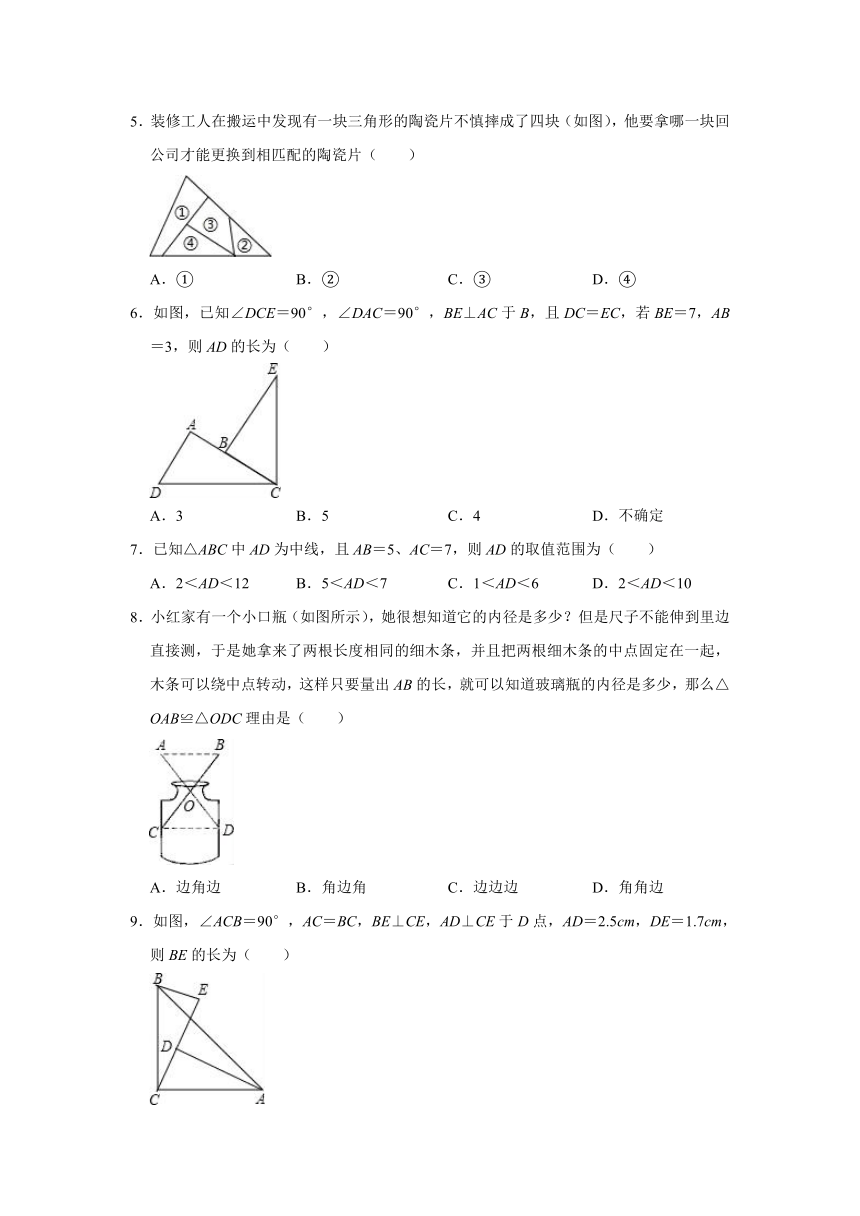
1.如图,点D在线段BC上,若∠ACE=180°﹣∠ABC﹣2x°,且BC=DE,AC=DC,AB=EC,则下列角中,大小为x°的角是( )
A.∠EFC B.∠ABC C.∠FDC D.∠DFC
2.如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AB=AB C.∠ABC=∠ABD D.∠BAC=∠BAD
3.如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
A.∠B=∠C B.BE=CD C.BD=CE D.∠ADC=∠AEB
4.用尺规作图,不能作出唯一三角形的是( )
A.已知两角和夹边
B.已知两边和其中一边的对角
C.已知两边和夹角
D.已知两角和其中一角的对边
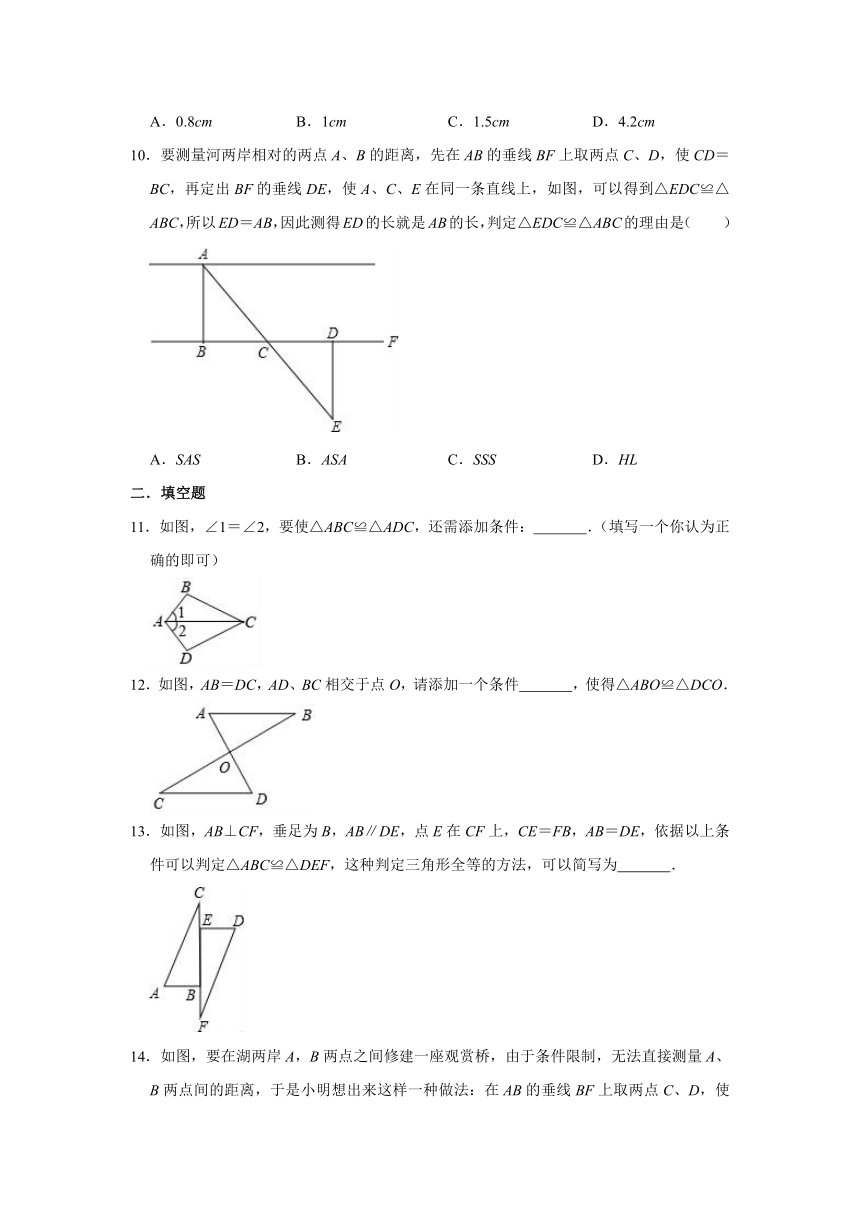
5.装修工人在搬运中发现有一块三角形的陶瓷片不慎摔成了四块(如图),他要拿哪一块回公司才能更换到相匹配的陶瓷片( )
A.① B.② C.③ D.④
6.如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC,若BE=7,AB=3,则AD的长为( )
A.3 B.5 C.4 D.不确定
7.已知△ABC中AD为中线,且AB=5、AC=7,则AD的取值范围为( )
A.2<AD<12 B.5<AD<7 C.1<AD<6 D.2<AD<10
8.小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸到里边直接测,于是她拿来了两根长度相同的细木条,并且把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△ODC理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
9.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D点,AD=2.5cm,DE=1.7cm,则BE的长为( )
A.0.8cm B.1cm C.1.5cm D.4.2cm
10.要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在同一条直线上,如图,可以得到△EDC≌△ABC,所以ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC的理由是( )
A.SAS B.ASA C.SSS D.HL
二.填空题
11.如图,∠1=∠2,要使△ABC≌△ADC,还需添加条件: .(填写一个你认为正确的即可)
12.如图,AB=DC,AD、BC相交于点O,请添加一个条件 ,使得△ABO≌△DCO.
13.如图,AB⊥CF,垂足为B,AB∥DE,点E在CF上,CE=FB,AB=DE,依据以上条件可以判定△ABC≌△DEF,这种判定三角形全等的方法,可以简写为 .
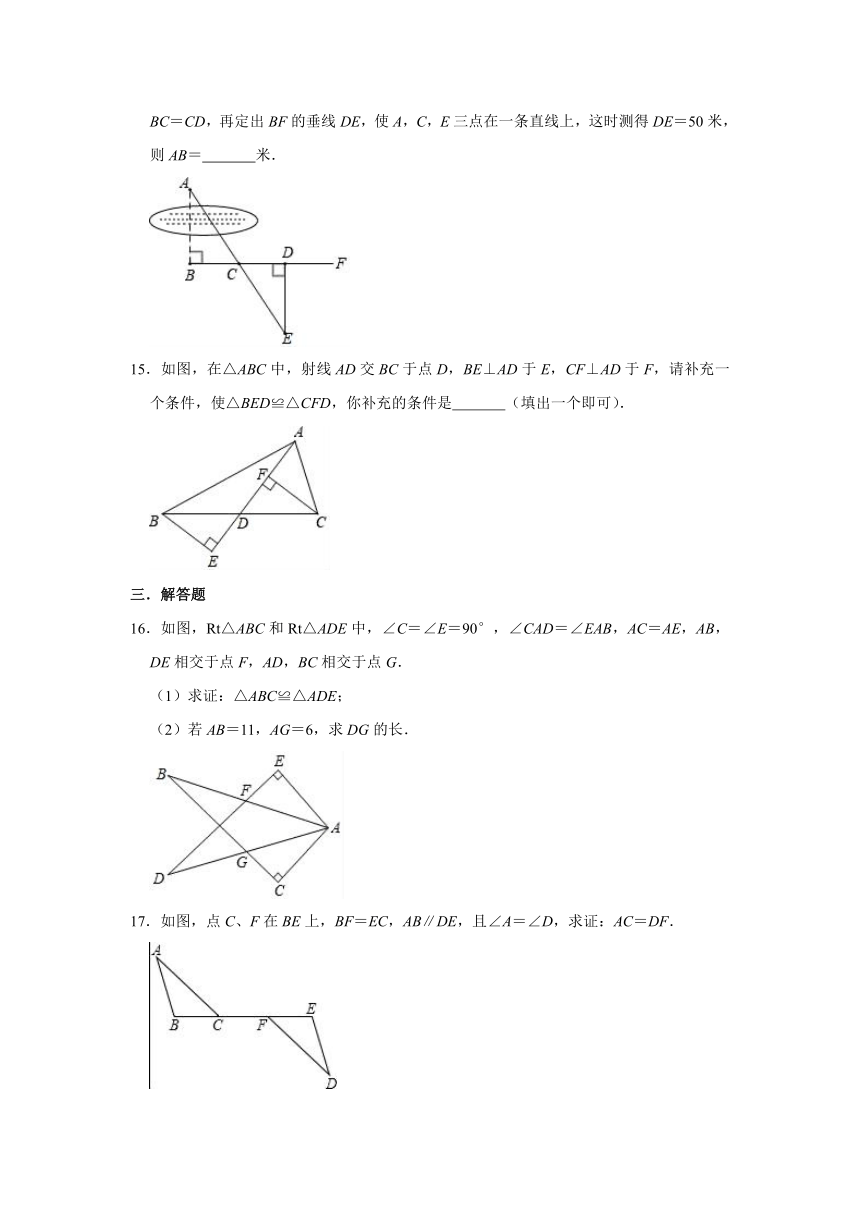
14.如图,要在湖两岸A,B两点之间修建一座观赏桥,由于条件限制,无法直接测量A、B两点间的距离,于是小明想出来这样一种做法:在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE=50米,则AB= 米.
15.如图,在△ABC中,射线AD交BC于点D,BE⊥AD于E,CF⊥AD于F,请补充一个条件,使△BED≌△CFD,你补充的条件是 (填出一个即可).
三.解答题
16.如图,Rt△ABC和Rt△ADE中,∠C=∠E=90°,∠CAD=∠EAB,AC=AE,AB,DE相交于点F,AD,BC相交于点G.
(1)求证:△ABC≌△ADE;
(2)若AB=11,AG=6,求DG的长.
17.如图,点C、F在BE上,BF=EC,AB∥DE,且∠A=∠D,求证:AC=DF.
18.如图,AE=AD,∠ABE=∠ACD,BE与CD相交于O.
(1)如图1,求证:AB=AC;
(2)如图2,连接BC、AO,请直接写出图2中所有的全等三角形(除△ABE≌△ACD外).
19.已知:直线m∥n,点A,B分别是直线m,n上任意两点,在直线n上取一点C,使BC=AB,连接AC,在直线AC上任取一点E,作∠BEF=∠ABC,EF交直线m于点F.
(1)如图1,若点E是线段AC上任意一点,EF交AB于H,求证:EF=BE;
(2)如图2,点E在线段AC的延长线上时,∠ABE与∠AFE互为补角,若∠ABC=90°,请判断线段EF与BE的数量关系,并说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:在△ABC和△CED中,
,
∴△ABC≌△CED(SSS),
∴∠B=∠E,∠ACB=∠EDC
∵∠ACE=180°﹣∠ABC﹣2x°=180°﹣∠E﹣∠CFE,
∴∠CFE=2x°,
∵∠EFC=∠FDC+∠FCD=2∠FDC,
∴∠FDC=x°,
故选:C.
2.【解答】解:需要添加的条件为BC=BD或AC=AD,理由为:
若添加的条件为BC=BD,
在Rt△ABC与Rt△ABD中,
∵,
∴Rt△ABC≌Rt△ABD(HL);
若添加的条件为AC=AD,
在Rt△ABC与Rt△ABD中,
∵,
∴Rt△ABC≌Rt△ABD(HL).
故选:A.
3.【解答】解:A、添加∠B=∠C可利用ASA定理判定△ABE≌△ACD,故此选项不合题意;
B、添加BE=CD不能判定△ABE≌△ACD,故此选项符合题意;
C、添加BD=CE可得AD=AE,可利用利用SAS定理判定△ABE≌△ACD,故此选项不合题意;
D、添加∠ADC=∠AEB可利用AAS定理判定△ABE≌△ACD,故此选项不合题意;
故选:B.
4.【解答】解:A、两角夹边(ASA)是成立的;
B、已知两边和其中一边的对角,不能证全等,故B是错误的;
C、两边夹角(SAS)是成立的;
D、已知两角和其中一角的对边(AAS)是成立的;
故选:B.
5.【解答】解:②、③、④块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第①块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选:A.
6.【解答】解:∵∠DCE=90°,
∴∠ACD+∠BCE=90°,
∵BE⊥AC,
∴∠CBE=90°,∠E+∠BCE=90°,
∴∠ACD=∠E,
在△ACD和△BCE中,
,
∴△ACD≌△BEC(AAS),
∴AD=BC,AC=BE=7,
∵AB=3,
∴BC=AC﹣AB=7﹣3=4.
故选:C.
7.【解答】解:
延长AD至点E,使DE=AD,连接EC,
在△ADB和△EDC中
∴△ADB≌△EDC(SAS),
∴CE=AB,
∵AB=5,AC=7,
∴CE=5,
设AD=x,则AE=2x,
∴7﹣5<2x<7+5,
∴1<x<6,
故选:C.
8.【解答】证明:在△AOB和△COD中,
,
∴△AOB≌△ODC(SAS),
∴AB=CD.
故选:A.
9.【解答】解:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中,
,
∴△CEB≌△ADC(AAS),
∴BE=DC.CE=AD=2.5.
∵DC=CE﹣DE,DE=1.7cm,
∴DC=2.5﹣1.7=0.8cm.
故选:A.
10.【解答】解:∵AB⊥BF,DE⊥BF,
∴∠ABC=∠EDC=90°,
在△EDC和△ABC中,
,
∴△EDC≌△ABC(ASA).
故选:B.
二.填空题(共5小题)
11.【解答】解:由已知可得,
∠1=∠2,AC=AC,
∴若添加条件AB=AC,则△ABC≌△ADC(SAS);
若添加条件∠ACB=∠ACD,则△ABC≌△ADC(ASA);
若添加条件∠ABC=∠ADC,则△ABC≌△ADC(AAS);
故答案为:AB=AC.
12.【解答】解:由题意可得,
AB=DC,∠AOB=∠DOC,
∴若添加条件∠A=∠D,则△ABO≌△DCO(AAS),
若添加条件∠B=∠C,则△ABO≌△DCO(AAS),
故答案为:∠A=∠D.
13.【解答】解:∵AB⊥CF,AB∥DE,
∴△ABC和△DEF都是直角三角形.
∵CE=FB,CE为公共部分,
∴CB=EF,
又∵AB=DE,
∴△ABC≌△DEF(SAS).
故答案为:SAS.
14.【解答】解:根据题意可知∠B=∠D=90°,BC=CD,∠ACB=∠ECD
∴△ABC≌△EDC(ASA)
∴AB=DE=50米.
故答案为:50
15.【解答】解:可以添加条件:BD=DC.
理由:∵BD=CD;
又∵BE⊥AD,CF⊥AD,
∴∠E=∠CFD=90°;
∴在△BED和△CFD中,
,
∴△BED≌△CFD(AAS).
故答案是:答案不唯一,如BD=DC.
三.解答题(共4小题)
16.【解答】(1)证明:∵∠CAD=∠EAB,
∴∠CAD+∠BAD=∠EAB+∠DAB,即∠CAB=∠EAD.
又AC=AE,∠C=∠E=90°,
∴△ABC≌△ADE(ASA);
(2)∵△ABC≌△ADE,
∴AB=AD.
∵AB=11,
∴AD=11.
又AG=6,
∴DG=11﹣6=5.
17.【解答】证明:∵BF=EC(已知),
即BC+CF=EF+FC,
∴BC=EF(等式性质).
∵AB∥DE,
∴∠B=∠E(两直线平行,内错角相等).
在△ABC和△DEF中
,
∴△ABC≌△DEF(AAS).
∴AC=DF(全等三角形对应边相等).
18.【解答】(1)证明:在△ABE和△ACD 中
,
∴△ABE≌△ACD (AAS),
∴AB=AC;
(2)解:∵AD=AE,
∴BD=CE,
而△ABE≌△ACD,
∴CD=BE,
∵BD=CE,CD=BE,BC=CB,
∴△BDC≌△CEB(SSS);
∴∠BCD=∠EBC,
∴OB=OC,
∴OD=OE,
而∠BOD=∠COE,
∴△DOB≌△EOC(SAS);
∵AB=AC,∠ABO=∠ACO,BO=CO,
∴△AOB≌△AOC(SAS);
∵AD=AE,OD=OE,AO=AO,
∴△ADO≌△AEO(SSS).
19.【解答】(1)证明:如图1,在直线m上,取点M,使ME=EA,
∴∠EMA=∠EAM,
∵BC=AB,
∴∠CAB=∠ACB,
∵m∥n,
∴∠MAC=∠ACB,∠FAB=∠ABC,
∴∠MAC=∠CAB,
∴∠CAB=∠EMA,
∵∠BEF=∠ABC,
∴∠FAB=∠BEF,
∵∠AHF=∠EHB
∴∠AFE=∠EBA,
∴△AEB≌△MEF(AAS),
∴EF=EB;
(2)解:EF=BE.
理由如下:如图2,在直线m上截取AN=AB,连接NE,
∵∠ABC=90°,
∴∠CAB=∠ACB=45°,
∵m∥n,
∴∠NAE=∠ACB=∠CAB=45°,∠FAB=90°,
∵AE=AE
∴△NAE≌△ABE(SAS),
∴EN=EB,∠ANE=∠ABE,
∵∠ABE+∠EFA=180°,∠ANE+∠ENF=180°
∴∠ENF=∠EFA,
∴EN=EF,
∴EF=BE.
一.选择题
1.如图,点D在线段BC上,若∠ACE=180°﹣∠ABC﹣2x°,且BC=DE,AC=DC,AB=EC,则下列角中,大小为x°的角是( )
A.∠EFC B.∠ABC C.∠FDC D.∠DFC
2.如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AB=AB C.∠ABC=∠ABD D.∠BAC=∠BAD
3.如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
A.∠B=∠C B.BE=CD C.BD=CE D.∠ADC=∠AEB
4.用尺规作图,不能作出唯一三角形的是( )
A.已知两角和夹边
B.已知两边和其中一边的对角
C.已知两边和夹角
D.已知两角和其中一角的对边
5.装修工人在搬运中发现有一块三角形的陶瓷片不慎摔成了四块(如图),他要拿哪一块回公司才能更换到相匹配的陶瓷片( )
A.① B.② C.③ D.④
6.如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC,若BE=7,AB=3,则AD的长为( )
A.3 B.5 C.4 D.不确定
7.已知△ABC中AD为中线,且AB=5、AC=7,则AD的取值范围为( )
A.2<AD<12 B.5<AD<7 C.1<AD<6 D.2<AD<10
8.小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸到里边直接测,于是她拿来了两根长度相同的细木条,并且把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△ODC理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
9.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D点,AD=2.5cm,DE=1.7cm,则BE的长为( )
A.0.8cm B.1cm C.1.5cm D.4.2cm
10.要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在同一条直线上,如图,可以得到△EDC≌△ABC,所以ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC的理由是( )
A.SAS B.ASA C.SSS D.HL
二.填空题
11.如图,∠1=∠2,要使△ABC≌△ADC,还需添加条件: .(填写一个你认为正确的即可)
12.如图,AB=DC,AD、BC相交于点O,请添加一个条件 ,使得△ABO≌△DCO.
13.如图,AB⊥CF,垂足为B,AB∥DE,点E在CF上,CE=FB,AB=DE,依据以上条件可以判定△ABC≌△DEF,这种判定三角形全等的方法,可以简写为 .
14.如图,要在湖两岸A,B两点之间修建一座观赏桥,由于条件限制,无法直接测量A、B两点间的距离,于是小明想出来这样一种做法:在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE=50米,则AB= 米.
15.如图,在△ABC中,射线AD交BC于点D,BE⊥AD于E,CF⊥AD于F,请补充一个条件,使△BED≌△CFD,你补充的条件是 (填出一个即可).
三.解答题
16.如图,Rt△ABC和Rt△ADE中,∠C=∠E=90°,∠CAD=∠EAB,AC=AE,AB,DE相交于点F,AD,BC相交于点G.
(1)求证:△ABC≌△ADE;
(2)若AB=11,AG=6,求DG的长.
17.如图,点C、F在BE上,BF=EC,AB∥DE,且∠A=∠D,求证:AC=DF.
18.如图,AE=AD,∠ABE=∠ACD,BE与CD相交于O.
(1)如图1,求证:AB=AC;
(2)如图2,连接BC、AO,请直接写出图2中所有的全等三角形(除△ABE≌△ACD外).
19.已知:直线m∥n,点A,B分别是直线m,n上任意两点,在直线n上取一点C,使BC=AB,连接AC,在直线AC上任取一点E,作∠BEF=∠ABC,EF交直线m于点F.
(1)如图1,若点E是线段AC上任意一点,EF交AB于H,求证:EF=BE;
(2)如图2,点E在线段AC的延长线上时,∠ABE与∠AFE互为补角,若∠ABC=90°,请判断线段EF与BE的数量关系,并说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:在△ABC和△CED中,
,
∴△ABC≌△CED(SSS),
∴∠B=∠E,∠ACB=∠EDC
∵∠ACE=180°﹣∠ABC﹣2x°=180°﹣∠E﹣∠CFE,
∴∠CFE=2x°,
∵∠EFC=∠FDC+∠FCD=2∠FDC,
∴∠FDC=x°,
故选:C.
2.【解答】解:需要添加的条件为BC=BD或AC=AD,理由为:
若添加的条件为BC=BD,
在Rt△ABC与Rt△ABD中,
∵,
∴Rt△ABC≌Rt△ABD(HL);
若添加的条件为AC=AD,
在Rt△ABC与Rt△ABD中,
∵,
∴Rt△ABC≌Rt△ABD(HL).
故选:A.
3.【解答】解:A、添加∠B=∠C可利用ASA定理判定△ABE≌△ACD,故此选项不合题意;
B、添加BE=CD不能判定△ABE≌△ACD,故此选项符合题意;
C、添加BD=CE可得AD=AE,可利用利用SAS定理判定△ABE≌△ACD,故此选项不合题意;
D、添加∠ADC=∠AEB可利用AAS定理判定△ABE≌△ACD,故此选项不合题意;
故选:B.
4.【解答】解:A、两角夹边(ASA)是成立的;
B、已知两边和其中一边的对角,不能证全等,故B是错误的;
C、两边夹角(SAS)是成立的;
D、已知两角和其中一角的对边(AAS)是成立的;
故选:B.
5.【解答】解:②、③、④块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第①块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选:A.
6.【解答】解:∵∠DCE=90°,
∴∠ACD+∠BCE=90°,
∵BE⊥AC,
∴∠CBE=90°,∠E+∠BCE=90°,
∴∠ACD=∠E,
在△ACD和△BCE中,
,
∴△ACD≌△BEC(AAS),
∴AD=BC,AC=BE=7,
∵AB=3,
∴BC=AC﹣AB=7﹣3=4.
故选:C.
7.【解答】解:
延长AD至点E,使DE=AD,连接EC,
在△ADB和△EDC中
∴△ADB≌△EDC(SAS),
∴CE=AB,
∵AB=5,AC=7,
∴CE=5,
设AD=x,则AE=2x,
∴7﹣5<2x<7+5,
∴1<x<6,
故选:C.
8.【解答】证明:在△AOB和△COD中,
,
∴△AOB≌△ODC(SAS),
∴AB=CD.
故选:A.
9.【解答】解:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中,
,
∴△CEB≌△ADC(AAS),
∴BE=DC.CE=AD=2.5.
∵DC=CE﹣DE,DE=1.7cm,
∴DC=2.5﹣1.7=0.8cm.
故选:A.
10.【解答】解:∵AB⊥BF,DE⊥BF,
∴∠ABC=∠EDC=90°,
在△EDC和△ABC中,
,
∴△EDC≌△ABC(ASA).
故选:B.
二.填空题(共5小题)
11.【解答】解:由已知可得,
∠1=∠2,AC=AC,
∴若添加条件AB=AC,则△ABC≌△ADC(SAS);
若添加条件∠ACB=∠ACD,则△ABC≌△ADC(ASA);
若添加条件∠ABC=∠ADC,则△ABC≌△ADC(AAS);
故答案为:AB=AC.
12.【解答】解:由题意可得,
AB=DC,∠AOB=∠DOC,
∴若添加条件∠A=∠D,则△ABO≌△DCO(AAS),
若添加条件∠B=∠C,则△ABO≌△DCO(AAS),
故答案为:∠A=∠D.
13.【解答】解:∵AB⊥CF,AB∥DE,
∴△ABC和△DEF都是直角三角形.
∵CE=FB,CE为公共部分,
∴CB=EF,
又∵AB=DE,
∴△ABC≌△DEF(SAS).
故答案为:SAS.
14.【解答】解:根据题意可知∠B=∠D=90°,BC=CD,∠ACB=∠ECD
∴△ABC≌△EDC(ASA)
∴AB=DE=50米.
故答案为:50
15.【解答】解:可以添加条件:BD=DC.
理由:∵BD=CD;
又∵BE⊥AD,CF⊥AD,
∴∠E=∠CFD=90°;
∴在△BED和△CFD中,
,
∴△BED≌△CFD(AAS).
故答案是:答案不唯一,如BD=DC.
三.解答题(共4小题)
16.【解答】(1)证明:∵∠CAD=∠EAB,
∴∠CAD+∠BAD=∠EAB+∠DAB,即∠CAB=∠EAD.
又AC=AE,∠C=∠E=90°,
∴△ABC≌△ADE(ASA);
(2)∵△ABC≌△ADE,
∴AB=AD.
∵AB=11,
∴AD=11.
又AG=6,
∴DG=11﹣6=5.
17.【解答】证明:∵BF=EC(已知),
即BC+CF=EF+FC,
∴BC=EF(等式性质).
∵AB∥DE,
∴∠B=∠E(两直线平行,内错角相等).
在△ABC和△DEF中
,
∴△ABC≌△DEF(AAS).
∴AC=DF(全等三角形对应边相等).
18.【解答】(1)证明:在△ABE和△ACD 中
,
∴△ABE≌△ACD (AAS),
∴AB=AC;
(2)解:∵AD=AE,
∴BD=CE,
而△ABE≌△ACD,
∴CD=BE,
∵BD=CE,CD=BE,BC=CB,
∴△BDC≌△CEB(SSS);
∴∠BCD=∠EBC,
∴OB=OC,
∴OD=OE,
而∠BOD=∠COE,
∴△DOB≌△EOC(SAS);
∵AB=AC,∠ABO=∠ACO,BO=CO,
∴△AOB≌△AOC(SAS);
∵AD=AE,OD=OE,AO=AO,
∴△ADO≌△AEO(SSS).
19.【解答】(1)证明:如图1,在直线m上,取点M,使ME=EA,
∴∠EMA=∠EAM,
∵BC=AB,
∴∠CAB=∠ACB,
∵m∥n,
∴∠MAC=∠ACB,∠FAB=∠ABC,
∴∠MAC=∠CAB,
∴∠CAB=∠EMA,
∵∠BEF=∠ABC,
∴∠FAB=∠BEF,
∵∠AHF=∠EHB
∴∠AFE=∠EBA,
∴△AEB≌△MEF(AAS),
∴EF=EB;
(2)解:EF=BE.
理由如下:如图2,在直线m上截取AN=AB,连接NE,
∵∠ABC=90°,
∴∠CAB=∠ACB=45°,
∵m∥n,
∴∠NAE=∠ACB=∠CAB=45°,∠FAB=90°,
∵AE=AE
∴△NAE≌△ABE(SAS),
∴EN=EB,∠ANE=∠ABE,
∵∠ABE+∠EFA=180°,∠ANE+∠ENF=180°
∴∠ENF=∠EFA,
∴EN=EF,
∴EF=BE.
