人教版数学九年级上册 第24章 24.2点和圆、直线和圆的位置关系同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级上册 第24章 24.2点和圆、直线和圆的位置关系同步测试试题(一)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 344.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 19:58:24 | ||
图片预览



文档简介
点和圆、直线和圆的位置关系同步测试试题(一)
一.选择题
1.用反证法证明:“一个三角形中,至少有一个内角大于或等于60°”.应假设( )
A.一个三角形中没有一个角大于或等于60°
B.一个三角形中至少有一个角小于60°
C.一个三角形中三个角都大于等于60°
D.一个三角形中有一个角大于等于60°
2.已知⊙A与⊙B外切,⊙C与⊙A、⊙B都内切,且AB=5,AC=6,BC=7,那么⊙C的半径长是( )
A.11 B.10 C.9 D.8
3.如图是某商品标牌的示意图,⊙O与等边△ABC的边BC相切于点C,且⊙O的直径与△ABC的高相等,已知等边△ABC边长为4,设⊙O与AC相交于点E,则AE的长为( )
A. B.1 C.﹣1 D.
4.如图,线段AB=6,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )
A.6 B. C.2 D.3
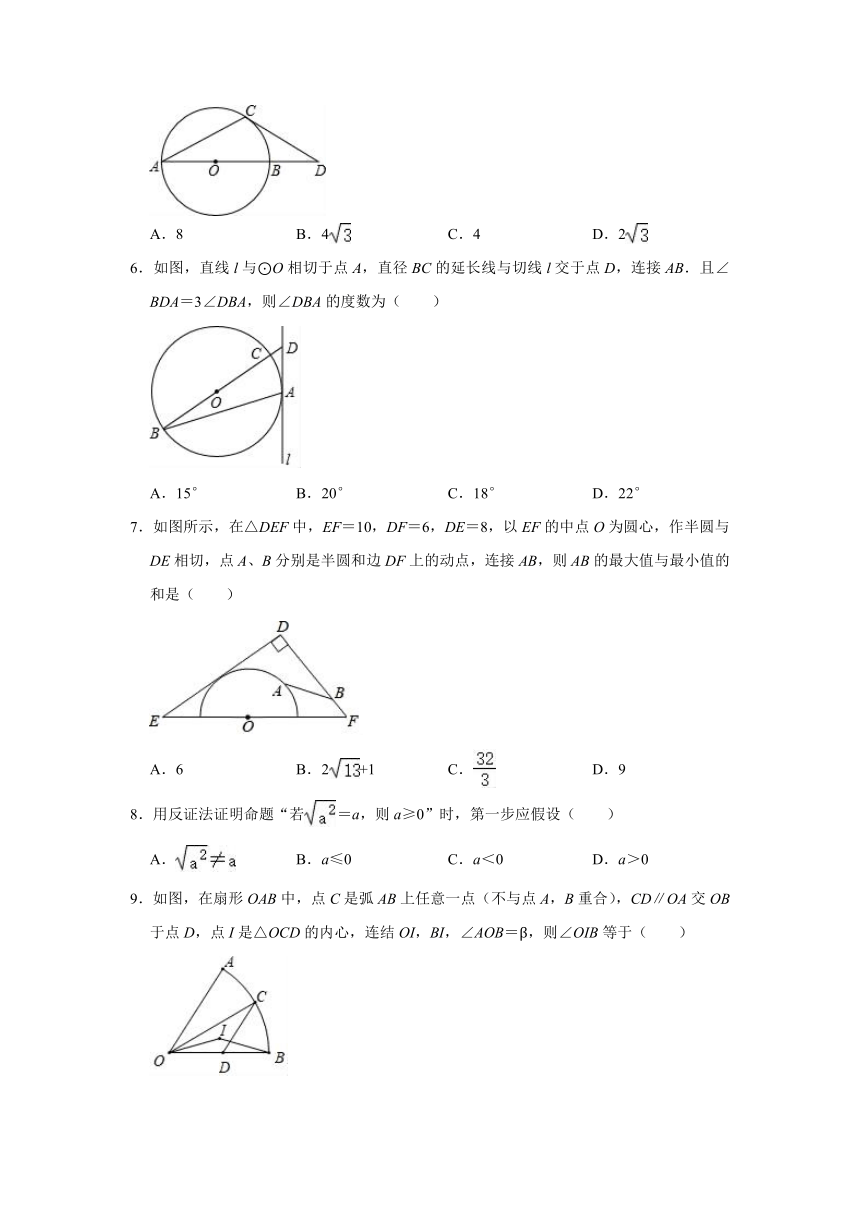
5.如图,圆O半径为4,AB是圆O的直径,C是圆O上的一点,D是AB延长线上一点,DC是圆O的切线,∠CAB=30°,则CD长( )
A.8 B.4 C.4 D.2
6.如图,直线l与⊙O相切于点A,直径BC的延长线与切线l交于点D,连接AB.且∠BDA=3∠DBA,则∠DBA的度数为( )
A.15° B.20° C.18° D.22°
7.如图所示,在△DEF中,EF=10,DF=6,DE=8,以EF的中点O为圆心,作半圆与DE相切,点A、B分别是半圆和边DF上的动点,连接AB,则AB的最大值与最小值的和是( )
A.6 B.2+1 C. D.9
8.用反证法证明命题“若=a,则a≥0”时,第一步应假设( )
A. B.a≤0 C.a<0 D.a>0
9.如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I是△OCD的内心,连结OI,BI,∠AOB=β,则∠OIB等于( )
A. B.180°﹣β C. D.90°+β
10.已知△ABC内接于⊙O,连接OA,OB,OC,设∠OAC=α,∠OBA=β,∠OCB=γ.则下列叙述中正确的有( )
①若α<β,α<γ,且OC∥AB,则γ=90°﹣α;
②若α:β:γ=1:4:3,则∠ACB=30°;
③若β<α,β<γ,则α+γ﹣β=90°;
④若β<α,β<γ,则∠BAC+∠ABC=α+γ﹣2β.
A.① B.③④ C.①②③ D.①②③④
二.填空题
11.在Rt△ABC中,∠C=90°,AC=5,BC=3,则其外接圆的直径为 .
12.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,∠AOP= °.
13.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°.CE平分∠ACB交⊙O于E,交AB于点D,连接AE,若△ADE的面积是5,则△CDB的面积是 .
14.如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD的延长线于点C,OE⊥AB于E,且AB=AC,若OE=,则CD= .
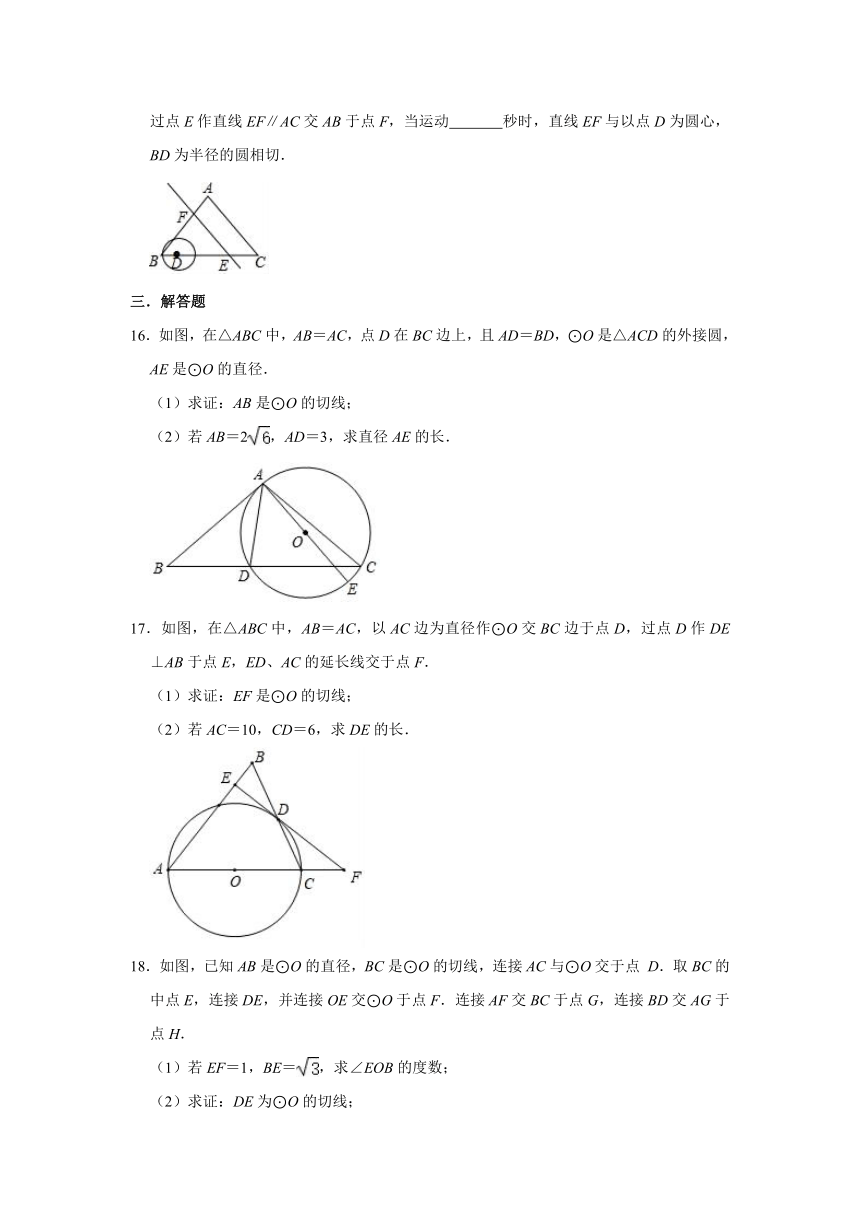
15.如图,△ABC中,BC=5,AC=4,S△ABC=,点D从点B开始以每秒1个单位的速度沿BC向点C运动,同时点E从点C开始以每秒2个单位的速度沿CB向点B运动,过点E作直线EF∥AC交AB于点F,当运动 秒时,直线EF与以点D为圆心,BD为半径的圆相切.
三.解答题
16.如图,在△ABC中,AB=AC,点D在BC边上,且AD=BD,⊙O是△ACD的外接圆,AE是⊙O的直径.
(1)求证:AB是⊙O的切线;
(2)若AB=2,AD=3,求直径AE的长.
17.如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若AC=10,CD=6,求DE的长.
18.如图,已知AB是⊙O的直径,BC是⊙O的切线,连接AC与⊙O交于点 D.取BC的中点E,连接DE,并连接OE交⊙O于点F.连接AF交BC于点G,连接BD交AG于点H.
(1)若EF=1,BE=,求∠EOB的度数;
(2)求证:DE为⊙O的切线;
(3)求证:点F为线段HG的中点.
19.如图,在Rt△ABC中,∠ACB=90°,AD为∠CAB的平分线,点O在AB上,⊙O经过点A,D两点,与AC,AB分别交于点E,F
(1)求证:BC与⊙O相切;
(2)若AC=8,AF=10,求AD和BC的长.
参考答案与试题解析
一.选择题
1.【解答】解:要证明原命题成立,则反证法假设的命题肯定不成立.从这一点出发,可以排除B,D这两个选项;反证法的核心是假设出原命题的相反面(或者说除原命题外的其他情况),证明假设的命题不成立,进而间接的证明原命题成立!原命题中出现“至少有一个”,则其对立面应该是“没有”、“不存在”、“没有一个”,所以应假设:一个三角形中没有一个角大于或等于60°
故选:A.
2.【解答】解:如图,设⊙A,⊙B,⊙C的半径为x,y,z.
由题意:,
解得,
故选:C.
3.【解答】解:连接OC,过点O作OF⊥CE于F,
∵△ABC为等边三角形,边长为4,
∴△ABC的高为2,即OC=,
∵⊙O与BC相切于点C,
∴OC⊥BC,
又∵∠ACB=60°,
∴∠OCF=30°,
在Rt△OFC中,FC=OCcos30°=×=,
∵OF过圆心,且OF⊥CE,
∴CE=2FC=3cm,
∴AE=4﹣3=1cm.
故选:B.
4.【解答】解:如图,分别作∠A与∠B角平分线,交点为P.
∵△ACD和△BCE都是等边三角形,
∴AP与BP为CD、CE垂直平分线.
又∵圆心O在CD、CE垂直平分线上,
∴∠OAB=∠OBA=30°,则交点P与圆心O重合,即圆心O是一个定点.
连接OC.
若半径OC最短,则OC⊥AB.
又∵∠OAC=∠OBC=30°,AB=6,
∴OA=OB,
∴AC=BC=3,
∴在直角△AOC中,OC=ACtan∠OAC=3×tan30°=.
故选:B.
5.【解答】解:连接OC,
∵DC是圆O切线,
∴∠OCD=90°,
∵OA=OC,
∴∠A=∠OCA=30°,
∴∠DOC=60°,
∴∠D=30°,
∴CD=OC=4.
故选:B.
6.【解答】解:连接OA.
∵OB=OA,
∴∠OBA=∠OAB,
∴∠DOA=2∠B,
∵∠BDA=3∠DBA,
∴设∠DBA=α,
∴∠DOA=2α,∠ADB=3α,
∵AD是⊙的切线,
∴∠OAD=90°.
∴2α+3α=90°,
∴α=18°.
∴∠DBA=18°,
故选:C.
7.【解答】解:如图所示,设⊙O与DE相切于点C,连接OC,作OB⊥DF于点B,交⊙O于点A,此时AB最小,为OB﹣OA,当A在N处,B在F处时,AB最大,就是FN的长,
∵EF=10,DF=6,DE=8,
∴EF2=DF2+DE2,
∴∠D=90°,
∵∠OBF=90°,
∴OB∥DE,
∵OE=OF,
∴OB=DE=4,BF=BD=3
由勾股定理得:OF=5
∵OC⊥DE,∠D=90°,
∴OC∥DF,
∵OE=OF,
∴OC=DF=3,
∴AB的最小值是:OB﹣OA=4﹣3=1,
AB的最大值是:FN=5+3=8,
∴AB的最大值与最小值的和是:8+1=9;
故选:D.
8.【解答】解:用反证法证明命题“若=a,则a≥0”时,第一步应假设a<0.
故选:C.
9.【解答】解:如图,连接IC,∵CD∥OA
∴∠CDB=∠AOB=β,
∴∠COD+∠OCD=∠CDB=β
∵点I是△OCD的内心
∴OI、CI分别平分∠COD、∠OCD
∴∠COI=∠BOI=∠COD,∠OCI=∠OCD
∴∠OIC=180°﹣(∠COI+∠OCI)=180°﹣(∠COD+∠OCD)=180°﹣β.
在△COI和△BOI中
∴△COI≌△BOI(SAS)
∴∠OIB=∠OIC
∴∠OIB=180°﹣β.
故选:A.
10.【解答】解:①如图1,∵OC∥AB,
∴∠BOC=∠OBA=β,∠AOC=180°﹣β,
∵OB=OC
∴∠OBC=∠OCB=γ
∵∠BOC+∠OBC+∠OCB=180°,即:β+γ+γ=180°
∴γ=90°﹣β,
∵∠AOC+∠OAC+∠OCA=180°,
∴180°﹣β+α+α=180°
∴β=2α
∴γ=90°﹣α
故①正确;
②如图2,∠OAC=∠OCA=α,∠OBA=∠OAB=β,∠OCB=∠OBC=γ
∵α:β:γ=1:4:3,设α=x°,β=4x°,γ=3x°
∴∠BAC=5x°,∠ABC=7x°,∠ACB=4x°,
∵∠BAC+∠ABC+∠ACB=180°
∴5x°+7x°+4x°=180°
∴x=
∴∠ACB=4x°=45°,
故②不正确.
③如图3,∵OA=OC=OB
∴∠OCA=∠OAC=α,∠OAB=∠OBA=β,∠OBC=∠OCB=γ
∴2(α+β+γ)=180°
∴α+β+γ=90°
故③不正确
④如图3,∠BAC+∠ABC=2α+β+γ≠α+γ﹣2β
故④不正确
故选:A.
二.填空题(共5小题)
11.【解答】解:在Rt△ABC中,
∵∠ACB=90°,AC=5,BC=3,
∴AB===,
∵直角三角形的外心为斜边中点,
∴Rt△ABC的外接圆的直径为.
故答案为:.
12.【解答】解:如图,
∵∠B和∠AOC都对,
∴∠AOC=2∠B=2×60°=120°,
∵OA=OC,OP⊥AC,
∴OP平分∠AOC,
∴∠AOP=AOC=×120°=60°.
故答案为60.
13.【解答】解:连接BE,
设AC=a,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=30°,
∴AB=2AC=2a,
由勾股定理得,BC==a,
∵CE平分∠ACB,
∴=,
∴AE=BE,
∴△AEB为等腰直角三角形,
∴AE=AB=a,
∵∠AEC=∠ABC,∠ADE=∠CDB,
∴△ADE∽△CDB,
∴=()2,即=,
解得,S△CDB=,
故答案为:.
14.【解答】解:连接OA、AD,
∵BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD延长线于点C,OE⊥AB于E,
∴∠DAB=90°,∠OAC=90°,
∴OE∥AD,
∵OD=OB,
∴OE=AD,
∴AD=2OE=2,
∵AB=AC,
∴∠B=∠C,
在△ACO和△BAD中,
,
∴△ACO≌△BAD(ASA),
∴AO=AD,
∵AO=OD,
∴AO=OD=AD,
∴△AOD是等边三角形,
∴∠ADO=∠DAO=60°,
∴∠B=∠C=30°,∠OAE=30°,∠DAC=30°,
∴CD=AD=2,
故答案为:2.
15.【解答】解:如图,作BM⊥AC于M,设直线EF与⊙D相切于点N,连接DN.
∵S△ABC=ACBM=,
∴BM=,
∵FE∥AC,
∴∠DEN=∠C,∵∠DNE=∠BMC,
∴△DNE∽△BMC,
∴=,
∴=,
∴DE=x,
∵BC=BD+DE+EC,
∴5=x+x+2x,
∴x=
故答案为.
三.解答题(共4小题)
16.【解答】(1)证明:连接DE,如图1,
∵AB=AC,AD=BD,
∴∠B=∠BAD,∠B=∠C,
∴∠C=∠E,
∴∠E=∠BAD,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠DAE=90°,
∴∠BAD+∠DAE=90°,
即∠BAE=90°,
∴直线AB是⊙O的切线;
(2)解:如图2,作AH⊥BC,垂足为点H,
∵AB=AC,
∴BH=CH,
∵∠B=∠C=∠BAD,
∴△ABC∽△DBA,
∴,
即AB2=BDBC,
又AB=2,BD=AD=3,
∴BC=6,
在Rt△ABH中,BH=CH=4,
∴AH===2,
∵∠E=∠B,∠ADE=∠AHB,
∴△AED∽△ABH,
∴,
∴=3.
17.【解答】(1)证明:连接OD,如图所示:
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB,
∴EF⊥OD,
又∵OD是⊙O的半径,
∴EF是⊙O的切线;
(2)解:连接AD,
∵AC为⊙O的直径,
∴∠ADC=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD=6.
在Rt△ACD中,AC=10,CD=6,
∴AD===8,
又∵DE⊥AB,AB=AC=10,
∴S△ABD=ABDE=ADBD,
即×10×DE=×8×6,
∴DE=4.8.
18.【解答】解:(1)∵AB是⊙O的直径,BC是⊙O的切线,
∴∠ABC=90°,
在直角三角形OBE中,设圆O半径为r,
∵EF=1,BE=,则,r2+()2=(r+1)2,
解得r=1,
∴OB=1,OE=2,
∴∠EOB=60°;
(2)连结OD,
∵AB是⊙O的直径,
∴∠ADB=∠BDC=90°,
∵E为直角三角形BCD斜边的中点,
∴DE=EC,
∴∠CDE=∠C,
∵OD=OA,
∴∠OAD=∠ODA,
∴∠ODA+∠CDE=∠OAD+∠C=90°,
∴∠ODE=180°﹣90°=90°,
∴DE是⊙O的切线;
(3)∵O、E分别为AB、BC的中点,
∴OE∥AC,
∵BD⊥AC,
∴OE⊥BD,
∴=,
∴∠FBD=∠FAB,
∵∠GBF=∠FAB,
∴∠FBD=∠GBF,
∴BF⊥HG,
∴BF平分HG,
即:点F为线段HG的中点.
19.【解答】(1)证明:连接OD.
∵OA=OD,
∴∠ODA=∠OAD.
又∵AD平分∠CAB,
∴∠CAD=∠BAD.
∴∠ODA=∠CAD,
∴OD∥AC,
∴∠ODB=∠ACB=90°,
∴OD⊥BC,
∴BC与⊙O相切;
(2)解:连接DF.
∵AF为直径,
∴∠ADF=90°,
∴∠ACD=∠ADF.
又∵∠CAD=∠FAD,
∴△CAD∽△DAF,
∴=,
∴AD2=CAAF=80,
∴AD=4,
在Rt△ACD中,CD==4.
∵OD∥AC,
∴△BOD∽△BAC,
∴=,
∴=,
∴BC=.
一.选择题
1.用反证法证明:“一个三角形中,至少有一个内角大于或等于60°”.应假设( )
A.一个三角形中没有一个角大于或等于60°
B.一个三角形中至少有一个角小于60°
C.一个三角形中三个角都大于等于60°
D.一个三角形中有一个角大于等于60°
2.已知⊙A与⊙B外切,⊙C与⊙A、⊙B都内切,且AB=5,AC=6,BC=7,那么⊙C的半径长是( )
A.11 B.10 C.9 D.8
3.如图是某商品标牌的示意图,⊙O与等边△ABC的边BC相切于点C,且⊙O的直径与△ABC的高相等,已知等边△ABC边长为4,设⊙O与AC相交于点E,则AE的长为( )
A. B.1 C.﹣1 D.
4.如图,线段AB=6,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )
A.6 B. C.2 D.3
5.如图,圆O半径为4,AB是圆O的直径,C是圆O上的一点,D是AB延长线上一点,DC是圆O的切线,∠CAB=30°,则CD长( )
A.8 B.4 C.4 D.2
6.如图,直线l与⊙O相切于点A,直径BC的延长线与切线l交于点D,连接AB.且∠BDA=3∠DBA,则∠DBA的度数为( )
A.15° B.20° C.18° D.22°
7.如图所示,在△DEF中,EF=10,DF=6,DE=8,以EF的中点O为圆心,作半圆与DE相切,点A、B分别是半圆和边DF上的动点,连接AB,则AB的最大值与最小值的和是( )
A.6 B.2+1 C. D.9
8.用反证法证明命题“若=a,则a≥0”时,第一步应假设( )
A. B.a≤0 C.a<0 D.a>0
9.如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I是△OCD的内心,连结OI,BI,∠AOB=β,则∠OIB等于( )
A. B.180°﹣β C. D.90°+β
10.已知△ABC内接于⊙O,连接OA,OB,OC,设∠OAC=α,∠OBA=β,∠OCB=γ.则下列叙述中正确的有( )
①若α<β,α<γ,且OC∥AB,则γ=90°﹣α;
②若α:β:γ=1:4:3,则∠ACB=30°;
③若β<α,β<γ,则α+γ﹣β=90°;
④若β<α,β<γ,则∠BAC+∠ABC=α+γ﹣2β.
A.① B.③④ C.①②③ D.①②③④
二.填空题
11.在Rt△ABC中,∠C=90°,AC=5,BC=3,则其外接圆的直径为 .
12.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,∠AOP= °.
13.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°.CE平分∠ACB交⊙O于E,交AB于点D,连接AE,若△ADE的面积是5,则△CDB的面积是 .
14.如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD的延长线于点C,OE⊥AB于E,且AB=AC,若OE=,则CD= .
15.如图,△ABC中,BC=5,AC=4,S△ABC=,点D从点B开始以每秒1个单位的速度沿BC向点C运动,同时点E从点C开始以每秒2个单位的速度沿CB向点B运动,过点E作直线EF∥AC交AB于点F,当运动 秒时,直线EF与以点D为圆心,BD为半径的圆相切.
三.解答题
16.如图,在△ABC中,AB=AC,点D在BC边上,且AD=BD,⊙O是△ACD的外接圆,AE是⊙O的直径.
(1)求证:AB是⊙O的切线;
(2)若AB=2,AD=3,求直径AE的长.
17.如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若AC=10,CD=6,求DE的长.
18.如图,已知AB是⊙O的直径,BC是⊙O的切线,连接AC与⊙O交于点 D.取BC的中点E,连接DE,并连接OE交⊙O于点F.连接AF交BC于点G,连接BD交AG于点H.
(1)若EF=1,BE=,求∠EOB的度数;
(2)求证:DE为⊙O的切线;
(3)求证:点F为线段HG的中点.
19.如图,在Rt△ABC中,∠ACB=90°,AD为∠CAB的平分线,点O在AB上,⊙O经过点A,D两点,与AC,AB分别交于点E,F
(1)求证:BC与⊙O相切;
(2)若AC=8,AF=10,求AD和BC的长.
参考答案与试题解析
一.选择题
1.【解答】解:要证明原命题成立,则反证法假设的命题肯定不成立.从这一点出发,可以排除B,D这两个选项;反证法的核心是假设出原命题的相反面(或者说除原命题外的其他情况),证明假设的命题不成立,进而间接的证明原命题成立!原命题中出现“至少有一个”,则其对立面应该是“没有”、“不存在”、“没有一个”,所以应假设:一个三角形中没有一个角大于或等于60°
故选:A.
2.【解答】解:如图,设⊙A,⊙B,⊙C的半径为x,y,z.
由题意:,
解得,
故选:C.
3.【解答】解:连接OC,过点O作OF⊥CE于F,
∵△ABC为等边三角形,边长为4,
∴△ABC的高为2,即OC=,
∵⊙O与BC相切于点C,
∴OC⊥BC,
又∵∠ACB=60°,
∴∠OCF=30°,
在Rt△OFC中,FC=OCcos30°=×=,
∵OF过圆心,且OF⊥CE,
∴CE=2FC=3cm,
∴AE=4﹣3=1cm.
故选:B.
4.【解答】解:如图,分别作∠A与∠B角平分线,交点为P.
∵△ACD和△BCE都是等边三角形,
∴AP与BP为CD、CE垂直平分线.
又∵圆心O在CD、CE垂直平分线上,
∴∠OAB=∠OBA=30°,则交点P与圆心O重合,即圆心O是一个定点.
连接OC.
若半径OC最短,则OC⊥AB.
又∵∠OAC=∠OBC=30°,AB=6,
∴OA=OB,
∴AC=BC=3,
∴在直角△AOC中,OC=ACtan∠OAC=3×tan30°=.
故选:B.
5.【解答】解:连接OC,
∵DC是圆O切线,
∴∠OCD=90°,
∵OA=OC,
∴∠A=∠OCA=30°,
∴∠DOC=60°,
∴∠D=30°,
∴CD=OC=4.
故选:B.
6.【解答】解:连接OA.
∵OB=OA,
∴∠OBA=∠OAB,
∴∠DOA=2∠B,
∵∠BDA=3∠DBA,
∴设∠DBA=α,
∴∠DOA=2α,∠ADB=3α,
∵AD是⊙的切线,
∴∠OAD=90°.
∴2α+3α=90°,
∴α=18°.
∴∠DBA=18°,
故选:C.
7.【解答】解:如图所示,设⊙O与DE相切于点C,连接OC,作OB⊥DF于点B,交⊙O于点A,此时AB最小,为OB﹣OA,当A在N处,B在F处时,AB最大,就是FN的长,
∵EF=10,DF=6,DE=8,
∴EF2=DF2+DE2,
∴∠D=90°,
∵∠OBF=90°,
∴OB∥DE,
∵OE=OF,
∴OB=DE=4,BF=BD=3
由勾股定理得:OF=5
∵OC⊥DE,∠D=90°,
∴OC∥DF,
∵OE=OF,
∴OC=DF=3,
∴AB的最小值是:OB﹣OA=4﹣3=1,
AB的最大值是:FN=5+3=8,
∴AB的最大值与最小值的和是:8+1=9;
故选:D.
8.【解答】解:用反证法证明命题“若=a,则a≥0”时,第一步应假设a<0.
故选:C.
9.【解答】解:如图,连接IC,∵CD∥OA
∴∠CDB=∠AOB=β,
∴∠COD+∠OCD=∠CDB=β
∵点I是△OCD的内心
∴OI、CI分别平分∠COD、∠OCD
∴∠COI=∠BOI=∠COD,∠OCI=∠OCD
∴∠OIC=180°﹣(∠COI+∠OCI)=180°﹣(∠COD+∠OCD)=180°﹣β.
在△COI和△BOI中
∴△COI≌△BOI(SAS)
∴∠OIB=∠OIC
∴∠OIB=180°﹣β.
故选:A.
10.【解答】解:①如图1,∵OC∥AB,
∴∠BOC=∠OBA=β,∠AOC=180°﹣β,
∵OB=OC
∴∠OBC=∠OCB=γ
∵∠BOC+∠OBC+∠OCB=180°,即:β+γ+γ=180°
∴γ=90°﹣β,
∵∠AOC+∠OAC+∠OCA=180°,
∴180°﹣β+α+α=180°
∴β=2α
∴γ=90°﹣α
故①正确;
②如图2,∠OAC=∠OCA=α,∠OBA=∠OAB=β,∠OCB=∠OBC=γ
∵α:β:γ=1:4:3,设α=x°,β=4x°,γ=3x°
∴∠BAC=5x°,∠ABC=7x°,∠ACB=4x°,
∵∠BAC+∠ABC+∠ACB=180°
∴5x°+7x°+4x°=180°
∴x=
∴∠ACB=4x°=45°,
故②不正确.
③如图3,∵OA=OC=OB
∴∠OCA=∠OAC=α,∠OAB=∠OBA=β,∠OBC=∠OCB=γ
∴2(α+β+γ)=180°
∴α+β+γ=90°
故③不正确
④如图3,∠BAC+∠ABC=2α+β+γ≠α+γ﹣2β
故④不正确
故选:A.
二.填空题(共5小题)
11.【解答】解:在Rt△ABC中,
∵∠ACB=90°,AC=5,BC=3,
∴AB===,
∵直角三角形的外心为斜边中点,
∴Rt△ABC的外接圆的直径为.
故答案为:.
12.【解答】解:如图,
∵∠B和∠AOC都对,
∴∠AOC=2∠B=2×60°=120°,
∵OA=OC,OP⊥AC,
∴OP平分∠AOC,
∴∠AOP=AOC=×120°=60°.
故答案为60.
13.【解答】解:连接BE,
设AC=a,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=30°,
∴AB=2AC=2a,
由勾股定理得,BC==a,
∵CE平分∠ACB,
∴=,
∴AE=BE,
∴△AEB为等腰直角三角形,
∴AE=AB=a,
∵∠AEC=∠ABC,∠ADE=∠CDB,
∴△ADE∽△CDB,
∴=()2,即=,
解得,S△CDB=,
故答案为:.
14.【解答】解:连接OA、AD,
∵BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD延长线于点C,OE⊥AB于E,
∴∠DAB=90°,∠OAC=90°,
∴OE∥AD,
∵OD=OB,
∴OE=AD,
∴AD=2OE=2,
∵AB=AC,
∴∠B=∠C,
在△ACO和△BAD中,
,
∴△ACO≌△BAD(ASA),
∴AO=AD,
∵AO=OD,
∴AO=OD=AD,
∴△AOD是等边三角形,
∴∠ADO=∠DAO=60°,
∴∠B=∠C=30°,∠OAE=30°,∠DAC=30°,
∴CD=AD=2,
故答案为:2.
15.【解答】解:如图,作BM⊥AC于M,设直线EF与⊙D相切于点N,连接DN.
∵S△ABC=ACBM=,
∴BM=,
∵FE∥AC,
∴∠DEN=∠C,∵∠DNE=∠BMC,
∴△DNE∽△BMC,
∴=,
∴=,
∴DE=x,
∵BC=BD+DE+EC,
∴5=x+x+2x,
∴x=
故答案为.
三.解答题(共4小题)
16.【解答】(1)证明:连接DE,如图1,
∵AB=AC,AD=BD,
∴∠B=∠BAD,∠B=∠C,
∴∠C=∠E,
∴∠E=∠BAD,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠DAE=90°,
∴∠BAD+∠DAE=90°,
即∠BAE=90°,
∴直线AB是⊙O的切线;
(2)解:如图2,作AH⊥BC,垂足为点H,
∵AB=AC,
∴BH=CH,
∵∠B=∠C=∠BAD,
∴△ABC∽△DBA,
∴,
即AB2=BDBC,
又AB=2,BD=AD=3,
∴BC=6,
在Rt△ABH中,BH=CH=4,
∴AH===2,
∵∠E=∠B,∠ADE=∠AHB,
∴△AED∽△ABH,
∴,
∴=3.
17.【解答】(1)证明:连接OD,如图所示:
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB,
∴EF⊥OD,
又∵OD是⊙O的半径,
∴EF是⊙O的切线;
(2)解:连接AD,
∵AC为⊙O的直径,
∴∠ADC=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD=6.
在Rt△ACD中,AC=10,CD=6,
∴AD===8,
又∵DE⊥AB,AB=AC=10,
∴S△ABD=ABDE=ADBD,
即×10×DE=×8×6,
∴DE=4.8.
18.【解答】解:(1)∵AB是⊙O的直径,BC是⊙O的切线,
∴∠ABC=90°,
在直角三角形OBE中,设圆O半径为r,
∵EF=1,BE=,则,r2+()2=(r+1)2,
解得r=1,
∴OB=1,OE=2,
∴∠EOB=60°;
(2)连结OD,
∵AB是⊙O的直径,
∴∠ADB=∠BDC=90°,
∵E为直角三角形BCD斜边的中点,
∴DE=EC,
∴∠CDE=∠C,
∵OD=OA,
∴∠OAD=∠ODA,
∴∠ODA+∠CDE=∠OAD+∠C=90°,
∴∠ODE=180°﹣90°=90°,
∴DE是⊙O的切线;
(3)∵O、E分别为AB、BC的中点,
∴OE∥AC,
∵BD⊥AC,
∴OE⊥BD,
∴=,
∴∠FBD=∠FAB,
∵∠GBF=∠FAB,
∴∠FBD=∠GBF,
∴BF⊥HG,
∴BF平分HG,
即:点F为线段HG的中点.
19.【解答】(1)证明:连接OD.
∵OA=OD,
∴∠ODA=∠OAD.
又∵AD平分∠CAB,
∴∠CAD=∠BAD.
∴∠ODA=∠CAD,
∴OD∥AC,
∴∠ODB=∠ACB=90°,
∴OD⊥BC,
∴BC与⊙O相切;
(2)解:连接DF.
∵AF为直径,
∴∠ADF=90°,
∴∠ACD=∠ADF.
又∵∠CAD=∠FAD,
∴△CAD∽△DAF,
∴=,
∴AD2=CAAF=80,
∴AD=4,
在Rt△ACD中,CD==4.
∵OD∥AC,
∴△BOD∽△BAC,
∴=,
∴=,
∴BC=.
同课章节目录
