人教版数学九年级上册 第25章概率初步单元测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级上册 第25章概率初步单元测试试题(一)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 213.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 20:04:47 | ||
图片预览




文档简介
概率初步单元测试试题(一)
一.选择题
1.下列事件中,必然事件是( )
A.2月份有31天
B.一个等腰三角形中,有两条边相等
C.明天的太阳从西边出来
D.投掷一枚质地均匀的骰子,出现6点朝上
2.下列说法正确的是( )
A.端午节我们有吃棕子的习俗,为了保证大家吃上放心的棕子,质监部门对广安市市场上的棕子实行全面调查
B.一组数据﹣1,2,5,7,7,7,4的众数是7,中位数是7
C.海底捞月是必然事件
D.甲、乙两名同学各跳远10次,若他们跳远成绩的平均数相同,甲同学跳远成绩的方差为1.2,乙同学跳远成绩的方差为1.6,则甲同学发挥比乙同学稳定
3.一枚质地均匀的普通骰子,抛掷6次没有1次点数1朝上,那么第7次抛掷,点数1朝上的概率是( )
A. B. C.1 D.0
4.在一个不透明的袋子里装有若干个白球和15个黄球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过很多次重复试验,发现摸到黄球的频率稳定在0.75,则袋中白球有( )
A.5个 B.15个 C.20个 D.35个
5.下列成语表示随机事件的是( )
A.水中捞月 B.水滴石穿 C.瓮中捉鳖 D.守株待兔
6.正方形地板由9块边长均相等的小正方形组成,米粒随机地撒在如图所示的正方形地板上,那么米粒最终停留在黑色区域的概率是( )
A. B. C. D.
7.一枚质地均匀的正方体骰子,其六个面上分别刻有1,2,3,4,5,6六个数字,投掷这个骰子一次,得到的点数与3,4作为等腰三角形三边的长,能构成等腰三角形的概率是( )
A. B. C. D.
8.春节期间,《中国诗词大会)节目的播出深受观众喜爱,进一步激起了人们对古诗词的喜爱,现有以下四句古诗词:①锄禾日当午;②春眠不觉晓;③白日依山尽;④床前明月光,甲、乙两名同学从中各随机选取了一句写在了纸上,则他们选取的诗句恰好相同的概率为( )
A. B. C. D.
9.小明要用如图的两个转盘做“配紫色”游戏,每个转盘均被等分成若干个扇形,他同时转动两个转盘,停止时指针所指的颜色恰好配成紫色的概率为( )
A. B. C. D.
10.一部记录片播放了关于地震的资料及一个有关地震预测的讨论,一位专家指出:“在未来20年,A城市发生地震的机会是三分之二”
对这位专家的陈述下面有四个推断:
①×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
②大于50%,所以未来20年,A城市一定发生地震;
③在未来20年,A城市发生地震的可能性大于不发生地震的可能性;
④不能确定在未来20年,A城市是否会发生地震;
其中合理的是( )
A.①③ B.②③ C.②④ D.③④
二.填空题
11.袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为”,则这个袋中白球大约有 个.
12.点P的坐标是(a,b),从﹣2,﹣1,1,2这四个数中任取一个数作为a的值,再从余下的三个数中任取一个数作b的值,则点P(a,b)在平面直角坐标系中第一象限内的概率是 .
13.在一个不透明的口袋中装有3个红球、1个黑球,这些球除颜色外其他都相同,在看不到球的条件下,随机地从这个袋子中摸出两个球,摸到的两个球都是红球的概率是 .
14.一个不透明的袋子中有4个分别标有数字6,2,﹣4,﹣1的球,这些球除所标的数字不同外其他都相同,若从袋子中随机摸出两个球,则这两个球上的两个数字之积为负数的概率是 .
15.如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为 .
三.解答题
16.甲、乙、丙三位同学在知识竞赛问答环节中,采用抽签的方式决定出场顺序.求甲比乙先出场的概率.
17.有四组家庭参加亲子活动,A、B、C、D分别代表四个家长,他们的孩子分别是a、b、c、d,若主持人随机从家长、孩子中各选择一个,请你用树状图或列表的方法求出选中的两人刚好是同一个家庭的概率.
18.“迎元旦大酬宾!”某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于60元的概率.
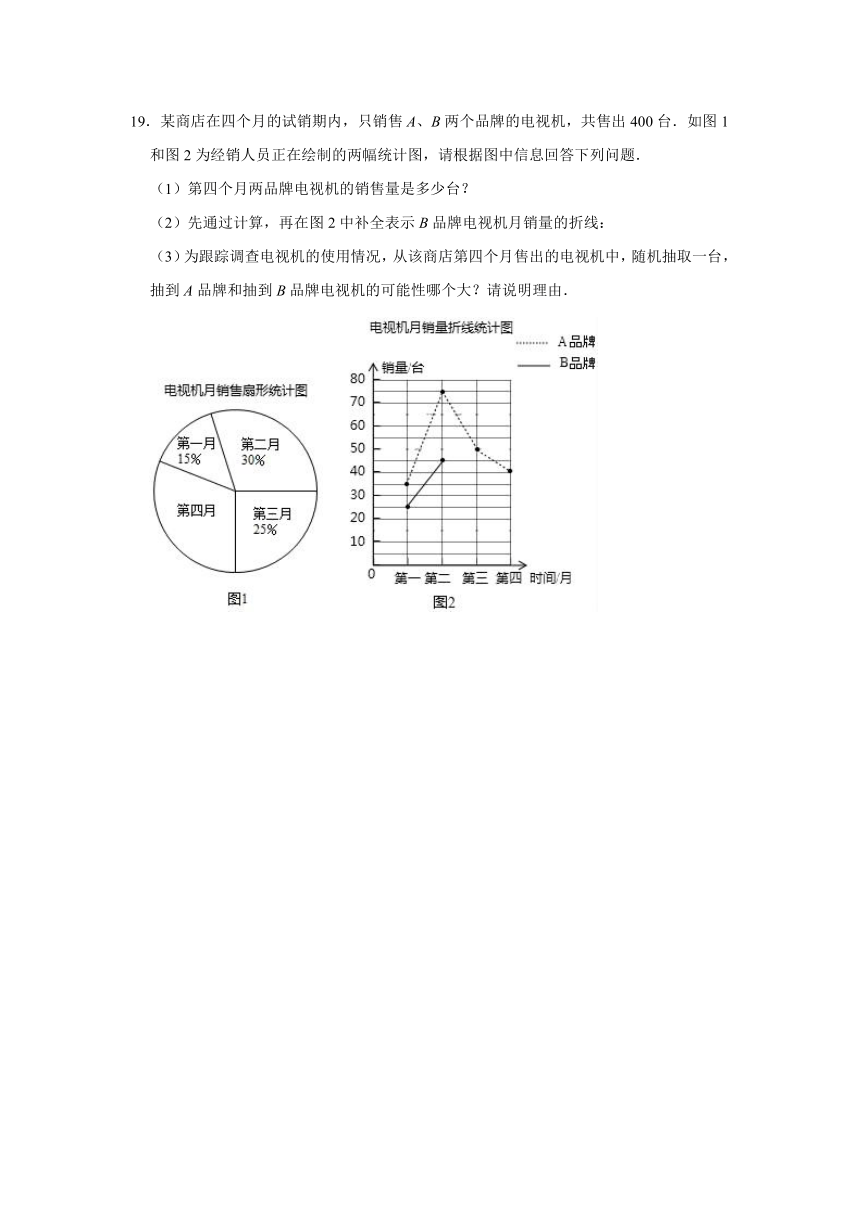
19.某商店在四个月的试销期内,只销售A、B两个品牌的电视机,共售出400台.如图1和图2为经销人员正在绘制的两幅统计图,请根据图中信息回答下列问题.
(1)第四个月两品牌电视机的销售量是多少台?
(2)先通过计算,再在图2中补全表示B品牌电视机月销量的折线:
(3)为跟踪调查电视机的使用情况,从该商店第四个月售出的电视机中,随机抽取一台,抽到A品牌和抽到B品牌电视机的可能性哪个大?请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、2月份有31天,是不可能事件;
B、一个等腰三角形中,有两条边相等,是必然事件;
C、明天的太阳从西边出来,是不可能事件;
D、投掷一枚质地均匀的骰子,出现6点朝上,是随机事件;
故选:B.
2.【解答】解:A、端午节我们有吃棕子的习俗,为了保证大家吃上放心的棕子,质监部门对广安市市场上的棕子实行抽样调查,本选项说法错误,不符合题意;
B、一组数据﹣1,2,5,7,7,7,4的众数是7,中位数是6,本选项说法错误,不符合题意;
C、海底捞月是不可能事件,本选项说法错误,不符合题意;
D、甲、乙两名同学各跳远10次,若他们跳远成绩的平均数相同,甲同学跳远成绩的方差为1.2,乙同学跳远成绩的方差为1.6,则甲同学发挥比乙同学稳定,本选项说法正确,符合题意;
故选:D.
3.【解答】解:∵抛掷一枚质地均匀的普通骰子,朝上一面共有6种等可能结果,其中点数1朝上的只有1种结果,
∴第7次抛掷,点数1朝上的概率是,
故选:A.
4.【解答】解:设袋中白球有x个,根据题意得:
=0.75,
解得:x=5,
经检验:x=5是分式方程的解,
故袋中白球有5个.
故选:A.
5.【解答】解:水中捞月是不可能事件,故选项A不符合题意;
B、水滴石穿是必然事件,故选项B不符合题意;
C、瓮中捉鳖是必然事件,故选项C不符合题意;
D、守株待兔是随机事件,故选项D符合题意;
故选:D.
6.【解答】解:∵由图可知,黑色方砖2块,共有9块方砖,
∴黑色方砖在整个地板中所占的面积的比值=,
∴米粒停在黑色区域的概率是.
故选:B.
7.【解答】解:画树状图为:
共有6种等可能的结果数,能构成等腰三角形的结果数为2,
所以能构成等腰三角形的概率==.
故选:C.
8.【解答】解:画树状图如下:
由树状图可知共有16种等可能结果,其中他们选取的诗句恰好相同的结果有4种,
∴他们选取的诗句恰好相同的概率为=,
故选:B.
9.【解答】解:根据题意列表如下:
白
蓝
红
红
(红,白)
(红,蓝)
(红,红)
蓝
(蓝,白)
(蓝,蓝)
(蓝,红)
上面等可能出现的6种结果中,有2种情况可能得到紫色,
故配成紫色的概率是=,
故选:C.
10.【解答】解:∵一位专家指出:在未来的20年,A市发生地震的机会是三分之二,
∴未来20年内,A市发生地震的可能性比没有发生地震的可能性大;不能确定在未来20年,A城市是否会发生地震,
故选:D.
二.填空题(共5小题)
11.【解答】解:∵袋中装有6个黑球和n个白球,
∴袋中一共有球(6+n)个,
∵从中任摸一个球,恰好是黑球的概率为,
∴=,
解得:n=2.
故答案为:2.
12.【解答】解:列树状图如图所示,
共12种情况;
∵点P(a,b)在平面直角坐标系中第一象限内,
∴a>0,b>0,
∴符合条件的有①a=1,b=2,②a=2,b=1,共2种情况,
∴点P(a,b)在平面直角坐标系中第一象限内的概率是=.
故答案为:.
13.【解答】解:树状图如图所示,
摸到的两个球都是红球的概率==,
故答案为
14.【解答】解:如图所示:
所有等可能的情况有12种,其中两个数字之积为负数的情况有8种,
P==,
故答案为:.
15.【解答】解:∵AB=15,BC=12,AC=9,
∴AB2=BC2+AC2,
∴△ABC为直角三角形,
∴△ABC的内切圆半径==3,
∴S△ABC=ACBC=×12×9=54,
S圆=9π,
∴小鸟落在花圃上的概率=,
故答案为:
三.解答题(共4小题)
16.【解答】解:画出树状图得:
∵共有6种等可能的结果,甲比乙先出场的有3种情况,
∴甲比乙先出场的概率为=.
17.【解答】解:用列表法表示所有可能出现的结果如下:
共有16种结果,每种结果出现的可能性相同,选中的两个人刚好是一个家庭的有4种,
选中的两人刚好是同一个家庭的概率为=.
18.【解答】解:(1)则该顾客至多可得到购物券:50+20=70(元);
故答案为:70;
(2)画树状图得:
∵共有12种等可能的结果,该顾客所获得购物券的金额不低于60元的有4种情况,
∴该顾客所获得购物券的金额不低于60元的概率为:=.
19.【解答】解:(1)根据题意得:400×(1﹣15%﹣30%﹣25%)=120(台),
答:第四个月两品牌电视机的销售量是120台;
(2)三月份的销售额是:400×25%=100(台),
则三月份B品牌电视机销量是100﹣50=50(台),
四月份B品牌电视机销量是400×30%﹣40=80(台),
补图如下:
(3)∵第四个月售出的电视机共有120台,其中销售A品牌有40台,B品牌有80台,
∴抽到A品牌的概率是=,抽到B品牌电视机的概率是=,
∴抽到B品牌电视机的可能性大.
一.选择题
1.下列事件中,必然事件是( )
A.2月份有31天
B.一个等腰三角形中,有两条边相等
C.明天的太阳从西边出来
D.投掷一枚质地均匀的骰子,出现6点朝上
2.下列说法正确的是( )
A.端午节我们有吃棕子的习俗,为了保证大家吃上放心的棕子,质监部门对广安市市场上的棕子实行全面调查
B.一组数据﹣1,2,5,7,7,7,4的众数是7,中位数是7
C.海底捞月是必然事件
D.甲、乙两名同学各跳远10次,若他们跳远成绩的平均数相同,甲同学跳远成绩的方差为1.2,乙同学跳远成绩的方差为1.6,则甲同学发挥比乙同学稳定
3.一枚质地均匀的普通骰子,抛掷6次没有1次点数1朝上,那么第7次抛掷,点数1朝上的概率是( )
A. B. C.1 D.0
4.在一个不透明的袋子里装有若干个白球和15个黄球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过很多次重复试验,发现摸到黄球的频率稳定在0.75,则袋中白球有( )
A.5个 B.15个 C.20个 D.35个
5.下列成语表示随机事件的是( )
A.水中捞月 B.水滴石穿 C.瓮中捉鳖 D.守株待兔
6.正方形地板由9块边长均相等的小正方形组成,米粒随机地撒在如图所示的正方形地板上,那么米粒最终停留在黑色区域的概率是( )
A. B. C. D.
7.一枚质地均匀的正方体骰子,其六个面上分别刻有1,2,3,4,5,6六个数字,投掷这个骰子一次,得到的点数与3,4作为等腰三角形三边的长,能构成等腰三角形的概率是( )
A. B. C. D.
8.春节期间,《中国诗词大会)节目的播出深受观众喜爱,进一步激起了人们对古诗词的喜爱,现有以下四句古诗词:①锄禾日当午;②春眠不觉晓;③白日依山尽;④床前明月光,甲、乙两名同学从中各随机选取了一句写在了纸上,则他们选取的诗句恰好相同的概率为( )
A. B. C. D.
9.小明要用如图的两个转盘做“配紫色”游戏,每个转盘均被等分成若干个扇形,他同时转动两个转盘,停止时指针所指的颜色恰好配成紫色的概率为( )
A. B. C. D.
10.一部记录片播放了关于地震的资料及一个有关地震预测的讨论,一位专家指出:“在未来20年,A城市发生地震的机会是三分之二”
对这位专家的陈述下面有四个推断:
①×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
②大于50%,所以未来20年,A城市一定发生地震;
③在未来20年,A城市发生地震的可能性大于不发生地震的可能性;
④不能确定在未来20年,A城市是否会发生地震;
其中合理的是( )
A.①③ B.②③ C.②④ D.③④
二.填空题
11.袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为”,则这个袋中白球大约有 个.
12.点P的坐标是(a,b),从﹣2,﹣1,1,2这四个数中任取一个数作为a的值,再从余下的三个数中任取一个数作b的值,则点P(a,b)在平面直角坐标系中第一象限内的概率是 .
13.在一个不透明的口袋中装有3个红球、1个黑球,这些球除颜色外其他都相同,在看不到球的条件下,随机地从这个袋子中摸出两个球,摸到的两个球都是红球的概率是 .
14.一个不透明的袋子中有4个分别标有数字6,2,﹣4,﹣1的球,这些球除所标的数字不同外其他都相同,若从袋子中随机摸出两个球,则这两个球上的两个数字之积为负数的概率是 .
15.如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为 .
三.解答题
16.甲、乙、丙三位同学在知识竞赛问答环节中,采用抽签的方式决定出场顺序.求甲比乙先出场的概率.
17.有四组家庭参加亲子活动,A、B、C、D分别代表四个家长,他们的孩子分别是a、b、c、d,若主持人随机从家长、孩子中各选择一个,请你用树状图或列表的方法求出选中的两人刚好是同一个家庭的概率.
18.“迎元旦大酬宾!”某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于60元的概率.
19.某商店在四个月的试销期内,只销售A、B两个品牌的电视机,共售出400台.如图1和图2为经销人员正在绘制的两幅统计图,请根据图中信息回答下列问题.
(1)第四个月两品牌电视机的销售量是多少台?
(2)先通过计算,再在图2中补全表示B品牌电视机月销量的折线:
(3)为跟踪调查电视机的使用情况,从该商店第四个月售出的电视机中,随机抽取一台,抽到A品牌和抽到B品牌电视机的可能性哪个大?请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、2月份有31天,是不可能事件;
B、一个等腰三角形中,有两条边相等,是必然事件;
C、明天的太阳从西边出来,是不可能事件;
D、投掷一枚质地均匀的骰子,出现6点朝上,是随机事件;
故选:B.
2.【解答】解:A、端午节我们有吃棕子的习俗,为了保证大家吃上放心的棕子,质监部门对广安市市场上的棕子实行抽样调查,本选项说法错误,不符合题意;
B、一组数据﹣1,2,5,7,7,7,4的众数是7,中位数是6,本选项说法错误,不符合题意;
C、海底捞月是不可能事件,本选项说法错误,不符合题意;
D、甲、乙两名同学各跳远10次,若他们跳远成绩的平均数相同,甲同学跳远成绩的方差为1.2,乙同学跳远成绩的方差为1.6,则甲同学发挥比乙同学稳定,本选项说法正确,符合题意;
故选:D.
3.【解答】解:∵抛掷一枚质地均匀的普通骰子,朝上一面共有6种等可能结果,其中点数1朝上的只有1种结果,
∴第7次抛掷,点数1朝上的概率是,
故选:A.
4.【解答】解:设袋中白球有x个,根据题意得:
=0.75,
解得:x=5,
经检验:x=5是分式方程的解,
故袋中白球有5个.
故选:A.
5.【解答】解:水中捞月是不可能事件,故选项A不符合题意;
B、水滴石穿是必然事件,故选项B不符合题意;
C、瓮中捉鳖是必然事件,故选项C不符合题意;
D、守株待兔是随机事件,故选项D符合题意;
故选:D.
6.【解答】解:∵由图可知,黑色方砖2块,共有9块方砖,
∴黑色方砖在整个地板中所占的面积的比值=,
∴米粒停在黑色区域的概率是.
故选:B.
7.【解答】解:画树状图为:
共有6种等可能的结果数,能构成等腰三角形的结果数为2,
所以能构成等腰三角形的概率==.
故选:C.
8.【解答】解:画树状图如下:
由树状图可知共有16种等可能结果,其中他们选取的诗句恰好相同的结果有4种,
∴他们选取的诗句恰好相同的概率为=,
故选:B.
9.【解答】解:根据题意列表如下:
白
蓝
红
红
(红,白)
(红,蓝)
(红,红)
蓝
(蓝,白)
(蓝,蓝)
(蓝,红)
上面等可能出现的6种结果中,有2种情况可能得到紫色,
故配成紫色的概率是=,
故选:C.
10.【解答】解:∵一位专家指出:在未来的20年,A市发生地震的机会是三分之二,
∴未来20年内,A市发生地震的可能性比没有发生地震的可能性大;不能确定在未来20年,A城市是否会发生地震,
故选:D.
二.填空题(共5小题)
11.【解答】解:∵袋中装有6个黑球和n个白球,
∴袋中一共有球(6+n)个,
∵从中任摸一个球,恰好是黑球的概率为,
∴=,
解得:n=2.
故答案为:2.
12.【解答】解:列树状图如图所示,
共12种情况;
∵点P(a,b)在平面直角坐标系中第一象限内,
∴a>0,b>0,
∴符合条件的有①a=1,b=2,②a=2,b=1,共2种情况,
∴点P(a,b)在平面直角坐标系中第一象限内的概率是=.
故答案为:.
13.【解答】解:树状图如图所示,
摸到的两个球都是红球的概率==,
故答案为
14.【解答】解:如图所示:
所有等可能的情况有12种,其中两个数字之积为负数的情况有8种,
P==,
故答案为:.
15.【解答】解:∵AB=15,BC=12,AC=9,
∴AB2=BC2+AC2,
∴△ABC为直角三角形,
∴△ABC的内切圆半径==3,
∴S△ABC=ACBC=×12×9=54,
S圆=9π,
∴小鸟落在花圃上的概率=,
故答案为:
三.解答题(共4小题)
16.【解答】解:画出树状图得:
∵共有6种等可能的结果,甲比乙先出场的有3种情况,
∴甲比乙先出场的概率为=.
17.【解答】解:用列表法表示所有可能出现的结果如下:
共有16种结果,每种结果出现的可能性相同,选中的两个人刚好是一个家庭的有4种,
选中的两人刚好是同一个家庭的概率为=.
18.【解答】解:(1)则该顾客至多可得到购物券:50+20=70(元);
故答案为:70;
(2)画树状图得:
∵共有12种等可能的结果,该顾客所获得购物券的金额不低于60元的有4种情况,
∴该顾客所获得购物券的金额不低于60元的概率为:=.
19.【解答】解:(1)根据题意得:400×(1﹣15%﹣30%﹣25%)=120(台),
答:第四个月两品牌电视机的销售量是120台;
(2)三月份的销售额是:400×25%=100(台),
则三月份B品牌电视机销量是100﹣50=50(台),
四月份B品牌电视机销量是400×30%﹣40=80(台),
补图如下:
(3)∵第四个月售出的电视机共有120台,其中销售A品牌有40台,B品牌有80台,
∴抽到A品牌的概率是=,抽到B品牌电视机的概率是=,
∴抽到B品牌电视机的可能性大.
同课章节目录
