28.1 锐角三角函数 同步练习(含答案)
文档属性
| 名称 | 28.1 锐角三角函数 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 179.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 19:34:11 | ||
图片预览




文档简介
28.1 锐角三角函数
第1课时 正弦
1.如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB=( )
A. B. C. D.
2.已知△ABC中,AC=4,BC=3,AB=5,则sinA=( )
A. B. C. D.
3.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,c=3a,则sinA的值是( )
A. B. C.3 D.以上都不对
4.如图,在平面直角坐标系中,点A的坐标为(4,3),那么sinα的值是( )
2309495289560A.
B.
C.
D.
5.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinB的值是
6.根据图中数据,求sinC和sinB的值.
7.如图所示,在Rt△ABC中,∠ACB=90°,a∶c=2∶3,求sinA和sinB的值.
8.在△ABC中,∠C=90°,BC=6,sinA=,则AB边的长是 .
9.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
10.已知Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,且AB=2A′B′,则sinA与sinA′的关系为( )
A.sinA=2sinA′ B.sinA=sinA′
C.2sinA=sinA′ D.不确定
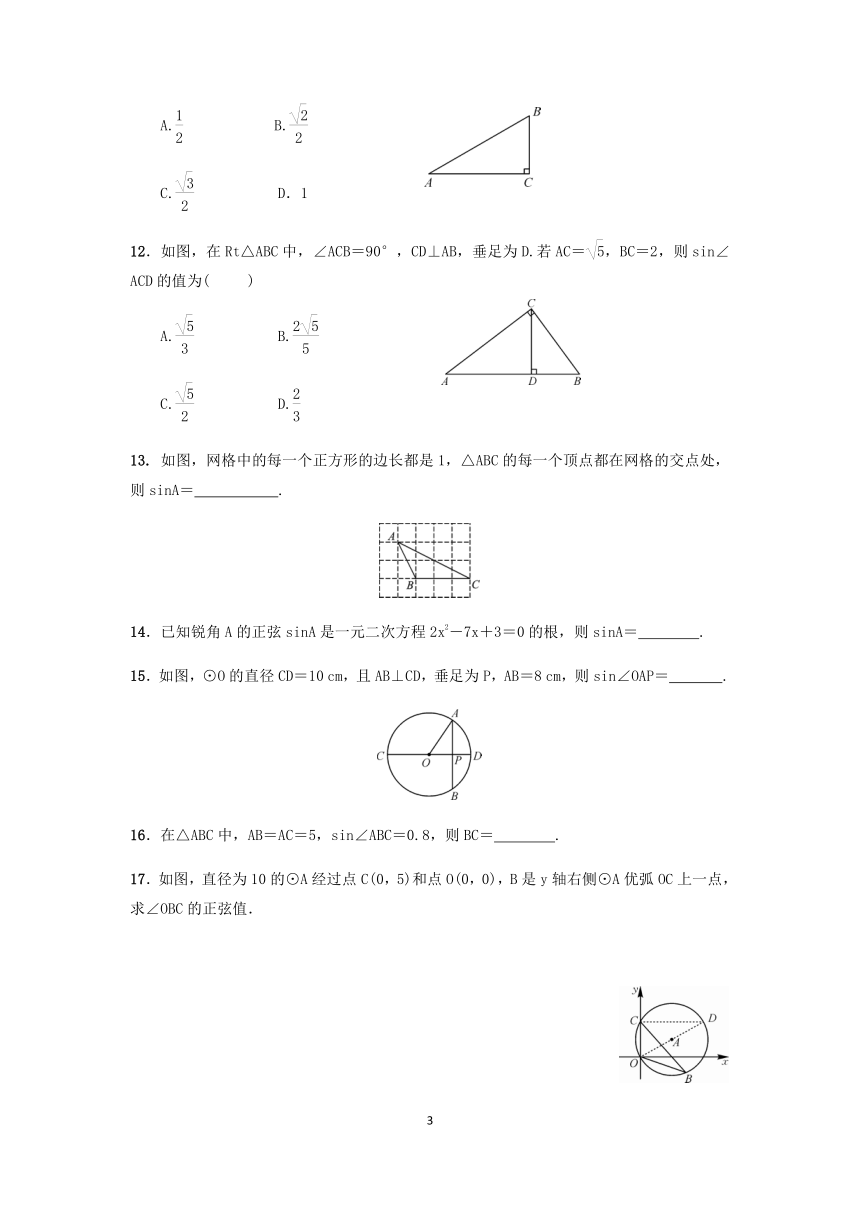
11.如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为( )
259143533655A. B.
C. D.1
273621552641512.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=,BC=2,则sin∠ACD的值为( )
A. B.
C. D.
13. 如图,网格中的每一个正方形的边长都是1,△ABC的每一个顶点都在网格的交点处,则sinA= .
14.已知锐角A的正弦sinA是一元二次方程2x2-7x+3=0的根,则sinA= .
15.如图,⊙O的直径CD=10 cm,且AB⊥CD,垂足为P,AB=8 cm,则sin∠OAP= .
16.在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC= .
17.如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧OC上一点,求∠OBC的正弦值.
18.如图,根据图中数据完成填空,再按要求答题:
sin2A1+sin2B1= ;sin2A2+sin2B2= ;sin2A3+sin2B3= .
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B= ;
(2)如图4,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理,证明你的猜想;
(3)已知在Rt△ABC中,∠A+∠B=90°,且sinA=,求sinB的值.
第2课时 锐角三角函数
30486351835151.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
A. B.
C. D.
2.在Rt△ABC中,∠C=90°,cosA=,AC=6 cm,那么BC等于( )
A.8 cm B. cm C. cm D. cm
3.在△ABC中,∠C=90°,AC=2,BC=1,求cosA和cosB的值.
4.在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )
A.3 B. C. D.
27514552190755.在4×4的正方形的网格中画出了如图所示的格点△ABC,则tan∠ABC的值为( )
A. B.
C. D.
6.如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 .
7.已知等腰三角形的腰长为6 cm,底边长为10 cm,则底角的正切值为.
8.如图,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB= .
29038551828809.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.sinA= B.cosA=
C.tanA= D.tanB=
10.在Rt△ABC中,∠C=90°,AC=7,BC=24.
(1)求AB的长;
(2)求sinA,cosA,tanA的值.
11.在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB=( )
A. B. C. D.
12.在Rt△ABC中,∠C=90°,若sinA=,则cosB的值是( )
A. B. C. D.
306387533337513.将△AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点A的坐标为(2,1),则tan∠A′OB′的值为( )
A. B.2
C. D.
14.在△ABC中,∠C=90°,若tanA=,则sinB= .
15.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是 .
16.如图,在半径为3的⊙O中,直径AB与弦CD交于点E,连接AC,BD.若AC=2,则cosD= .
17.如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
18.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD的点F处,如果=,求tan∠DCF的值.
19.如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作cotα,即cotα==,根据上述角的余切定义,解下列问题:
(1)cot30°=;
(2)如图,已知tanA=,其中∠A为锐角,试求cotA的值.
第3课时 特殊角的三角函数值
1.已知∠A=30°,下列判断正确的是( )
A.sinA= B.cosA=
C.tanA= D.以上都不对
2.2cos60°=( )
A.1 B. C. D.
3.计算:cos245°+sin245°=( )
A. B.1 C. D.
4.计算:tan45°+cos45°= .
5.计算:
(1)sin30°+cos45°;
(2)cos30°·tan30°-tan245°;
(3)sin45°+sin60°·cos45°.
6.在△ABC中,若|sinA-|+(cosB-)2=0,则∠C的度数是( )
A.30° B.45° C.60° D.90°
7.如果在△ABC中,sinA=cosB=,那么下列最确切的结论是( )
A.△ABC是直角三角形
B.△ABC是等腰三角形
C.△ABC是等腰直角三角形
D.△ABC是锐角三角形
8.已知α为锐角,且cos(90°-α)=,则α= .
9.在△ABC中,∠C=90°,AC=2,BC=2,则∠A= .
10.用计算器计算cos44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
261429549720511.如图,在△ABC中,∠C=90°,∠B=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.5÷tan26°=
B.5÷sin26°=
C.5×cos26°=
D.5×tan26°=
12.利用计算器求∠A=18°36′的三个锐角三角函数值.
13.已知下列正(余)弦值,用计算器求对应的锐角(精确到0.1°).
(1)sinα=0.822 1; (2)cosβ=0.843 4.
14.点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )
A.(,) B.(-,-)
C.(-,) D.(-,-)
15.李红同学遇到了这样一道题:tan(α+20°)=1,你猜想锐角α的度数应是( )
A.40° B.30° C.20° D.10°
16.如图,以点O为圆心,任意长为半径画弧,与射线OA交于点B,再以点B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
330454038100A. B.
C. D.
357441532131017.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为( )
A.(,1) B.(1,)
C.(+1,1) D.(1,+1)
18.如图,在△ABC中,∠C=90°,∠ABC=60°,D是AC的中点,那么tan∠DBC的值是 .
19.计算:
(1)2 0180+(-1)2-2tan45°+;
(2)(-1)-2+|-|+(π-3.14)0-tan60°+.
20.若tanA的值是方程x2-(1+)x+=0的一个根,求锐角A的度数.
29654505715021.如图,在等腰△ABC中,AB=AC=1.
(1)若BC=,求△ABC三个内角的度数;
(2)若BC=,求△ABC三个内角的度数.
22.(临沂中考)一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sinα·cosβ+cosα·sinβ;sin(α-β)=sinα·cosβ-cosα·sinβ.
例如:sin90°=sin(60°+30°)=sin60°·cos30°+cos60°·sin30°=×+×=1.类似地,可以求得sin15°的值是 .
参考答案:
第1课时 正弦
1.A
2.A
3.A
4.A
5. .
6.解:在Rt△ABC中,
BC==,
∴sinC==,
sinB==.
7.解:在Rt△ABC中,
∠ACB=90°,a∶c=2∶3,
设a=2k,c=3k.(k>0)
∴b==k.
∴sinA===,
sinB===.
8.9.
9.A
10.B
11.C
12.A
13. .
14..
15..
16.6.
17.解:连接OA并延长交⊙A于点D,连接CD.
∴∠OBC=∠ODC,
∠OCD=90°.
∴sin∠OBC=sin∠ODC===.
18.
sin2A1+sin2B1=1;sin2A2+sin2B2=1;sin2A3+sin2B3=1.
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B=1;
(2)如图4,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理,证明你的猜想;
(3)已知在Rt△ABC中,∠A+∠B=90°,且sinA=,求sinB的值.
解:(2)证明:∵在Rt△ABC中,∠C=90°,
sinA=,sinB=,
∴sin2A+sin2B=.
∵∠C=90°,
∴a2+b2=c2.
∴sin2A+sin2B=1.
(3)∵sinA=,sin2A+sin2B=1,且sinB>0,
∴sinB==.
第2课时 锐角三角函数
1.A
2.A
3.解:∵∠C=90°,AC=2,BC=1,
∴AB===.
∴cosA===,cosB===.
4.A
5.D
6. .
7..
8.17.
9.A
10.解:(1)由勾股定理,得
AB===25.
(2)sinA==,cosA==,
tanA==.
11.C
12.B
13.A
14..
15..
16..
17.解:在Rt△ACD中,CD=6,tanA=,
∴==,即AD=4.
又AB=12,
∴BD=AB-AD=8.
在Rt△BCD中,BC==10.
∴sinB===,cosB===.
∴sinB+cosB=+=.
18.解:∵四边形ABCD是矩形,
∴AB=CD,∠D=90°.
∵=,且由折叠知CF=BC,
∴=.
设CD=2x,CF=3x(x>0),
∴DF==x.
∴tan∠DCF===.
19.(1)cot30°=;
(2)解:∵tanA=,且tanA=,
∴设BC=3x,AC=4x.
∴cotA===.
第3课时 特殊角的三角函数值
1.A
2.A
3.B
4.2.
5.(1)sin30°+cos45°;
解:原式=+=.
(2)cos30°·tan30°-tan245°;
解:原式=×-12=-1=-.
(3)sin45°+sin60°·cos45°.
解:原式=×+×=.
6.D
7.C
8. 30°.
9. 60°.
10.B
11.D
12.解:sinA=sin18°36′≈0.319 0,
cosA=cos18°36′≈0.947 8,
tanA=tan18°36′≈0.336 5.
13.(1)sinα=0.822 1;
解:α≈55.3°.
(2)cosβ=0.843 4.
解:β≈32.5°.
14.B
15.D
16.D
17.C
18. .
19.(1)2 0180+(-1)2-2tan45°+;
解:原式=1+1-2×1+2
=2.
(2)(-1)-2+|-|+(π-3.14)0-tan60°+.
解:原式=1+(-)+1-+2
=2+.
20.解:解方程x2-(1+)x+=0,
得x1=1,x2=.
由题意知tanA=1或tanA=.
∴∠A=45°或60°.
21.解:(1)∵AB=AC=1,BC=,
∴AB2+AC2=BC2.
∴∠BAC=90°,∠B=∠C=45°.
(2)过点A作AD⊥BC,垂足为D.
∵AB=AC=1,AD⊥BC,
∴BD=BC=.
∴cosB===.
∴∠B=30°.
∴∠C=30°,∠BAC=120°.
22..
第1课时 正弦
1.如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB=( )
A. B. C. D.
2.已知△ABC中,AC=4,BC=3,AB=5,则sinA=( )
A. B. C. D.
3.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,c=3a,则sinA的值是( )
A. B. C.3 D.以上都不对
4.如图,在平面直角坐标系中,点A的坐标为(4,3),那么sinα的值是( )
2309495289560A.
B.
C.
D.
5.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinB的值是
6.根据图中数据,求sinC和sinB的值.
7.如图所示,在Rt△ABC中,∠ACB=90°,a∶c=2∶3,求sinA和sinB的值.
8.在△ABC中,∠C=90°,BC=6,sinA=,则AB边的长是 .
9.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
10.已知Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,且AB=2A′B′,则sinA与sinA′的关系为( )
A.sinA=2sinA′ B.sinA=sinA′
C.2sinA=sinA′ D.不确定
11.如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为( )
259143533655A. B.
C. D.1
273621552641512.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=,BC=2,则sin∠ACD的值为( )
A. B.
C. D.
13. 如图,网格中的每一个正方形的边长都是1,△ABC的每一个顶点都在网格的交点处,则sinA= .
14.已知锐角A的正弦sinA是一元二次方程2x2-7x+3=0的根,则sinA= .
15.如图,⊙O的直径CD=10 cm,且AB⊥CD,垂足为P,AB=8 cm,则sin∠OAP= .
16.在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC= .
17.如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧OC上一点,求∠OBC的正弦值.
18.如图,根据图中数据完成填空,再按要求答题:
sin2A1+sin2B1= ;sin2A2+sin2B2= ;sin2A3+sin2B3= .
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B= ;
(2)如图4,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理,证明你的猜想;
(3)已知在Rt△ABC中,∠A+∠B=90°,且sinA=,求sinB的值.
第2课时 锐角三角函数
30486351835151.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
A. B.
C. D.
2.在Rt△ABC中,∠C=90°,cosA=,AC=6 cm,那么BC等于( )
A.8 cm B. cm C. cm D. cm
3.在△ABC中,∠C=90°,AC=2,BC=1,求cosA和cosB的值.
4.在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )
A.3 B. C. D.
27514552190755.在4×4的正方形的网格中画出了如图所示的格点△ABC,则tan∠ABC的值为( )
A. B.
C. D.
6.如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 .
7.已知等腰三角形的腰长为6 cm,底边长为10 cm,则底角的正切值为.
8.如图,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB= .
29038551828809.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.sinA= B.cosA=
C.tanA= D.tanB=
10.在Rt△ABC中,∠C=90°,AC=7,BC=24.
(1)求AB的长;
(2)求sinA,cosA,tanA的值.
11.在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB=( )
A. B. C. D.
12.在Rt△ABC中,∠C=90°,若sinA=,则cosB的值是( )
A. B. C. D.
306387533337513.将△AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点A的坐标为(2,1),则tan∠A′OB′的值为( )
A. B.2
C. D.
14.在△ABC中,∠C=90°,若tanA=,则sinB= .
15.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是 .
16.如图,在半径为3的⊙O中,直径AB与弦CD交于点E,连接AC,BD.若AC=2,则cosD= .
17.如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
18.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD的点F处,如果=,求tan∠DCF的值.
19.如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作cotα,即cotα==,根据上述角的余切定义,解下列问题:
(1)cot30°=;
(2)如图,已知tanA=,其中∠A为锐角,试求cotA的值.
第3课时 特殊角的三角函数值
1.已知∠A=30°,下列判断正确的是( )
A.sinA= B.cosA=
C.tanA= D.以上都不对
2.2cos60°=( )
A.1 B. C. D.
3.计算:cos245°+sin245°=( )
A. B.1 C. D.
4.计算:tan45°+cos45°= .
5.计算:
(1)sin30°+cos45°;
(2)cos30°·tan30°-tan245°;
(3)sin45°+sin60°·cos45°.
6.在△ABC中,若|sinA-|+(cosB-)2=0,则∠C的度数是( )
A.30° B.45° C.60° D.90°
7.如果在△ABC中,sinA=cosB=,那么下列最确切的结论是( )
A.△ABC是直角三角形
B.△ABC是等腰三角形
C.△ABC是等腰直角三角形
D.△ABC是锐角三角形
8.已知α为锐角,且cos(90°-α)=,则α= .
9.在△ABC中,∠C=90°,AC=2,BC=2,则∠A= .
10.用计算器计算cos44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
261429549720511.如图,在△ABC中,∠C=90°,∠B=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.5÷tan26°=
B.5÷sin26°=
C.5×cos26°=
D.5×tan26°=
12.利用计算器求∠A=18°36′的三个锐角三角函数值.
13.已知下列正(余)弦值,用计算器求对应的锐角(精确到0.1°).
(1)sinα=0.822 1; (2)cosβ=0.843 4.
14.点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )
A.(,) B.(-,-)
C.(-,) D.(-,-)
15.李红同学遇到了这样一道题:tan(α+20°)=1,你猜想锐角α的度数应是( )
A.40° B.30° C.20° D.10°
16.如图,以点O为圆心,任意长为半径画弧,与射线OA交于点B,再以点B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
330454038100A. B.
C. D.
357441532131017.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为( )
A.(,1) B.(1,)
C.(+1,1) D.(1,+1)
18.如图,在△ABC中,∠C=90°,∠ABC=60°,D是AC的中点,那么tan∠DBC的值是 .
19.计算:
(1)2 0180+(-1)2-2tan45°+;
(2)(-1)-2+|-|+(π-3.14)0-tan60°+.
20.若tanA的值是方程x2-(1+)x+=0的一个根,求锐角A的度数.
29654505715021.如图,在等腰△ABC中,AB=AC=1.
(1)若BC=,求△ABC三个内角的度数;
(2)若BC=,求△ABC三个内角的度数.
22.(临沂中考)一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sinα·cosβ+cosα·sinβ;sin(α-β)=sinα·cosβ-cosα·sinβ.
例如:sin90°=sin(60°+30°)=sin60°·cos30°+cos60°·sin30°=×+×=1.类似地,可以求得sin15°的值是 .
参考答案:
第1课时 正弦
1.A
2.A
3.A
4.A
5. .
6.解:在Rt△ABC中,
BC==,
∴sinC==,
sinB==.
7.解:在Rt△ABC中,
∠ACB=90°,a∶c=2∶3,
设a=2k,c=3k.(k>0)
∴b==k.
∴sinA===,
sinB===.
8.9.
9.A
10.B
11.C
12.A
13. .
14..
15..
16.6.
17.解:连接OA并延长交⊙A于点D,连接CD.
∴∠OBC=∠ODC,
∠OCD=90°.
∴sin∠OBC=sin∠ODC===.
18.
sin2A1+sin2B1=1;sin2A2+sin2B2=1;sin2A3+sin2B3=1.
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B=1;
(2)如图4,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理,证明你的猜想;
(3)已知在Rt△ABC中,∠A+∠B=90°,且sinA=,求sinB的值.
解:(2)证明:∵在Rt△ABC中,∠C=90°,
sinA=,sinB=,
∴sin2A+sin2B=.
∵∠C=90°,
∴a2+b2=c2.
∴sin2A+sin2B=1.
(3)∵sinA=,sin2A+sin2B=1,且sinB>0,
∴sinB==.
第2课时 锐角三角函数
1.A
2.A
3.解:∵∠C=90°,AC=2,BC=1,
∴AB===.
∴cosA===,cosB===.
4.A
5.D
6. .
7..
8.17.
9.A
10.解:(1)由勾股定理,得
AB===25.
(2)sinA==,cosA==,
tanA==.
11.C
12.B
13.A
14..
15..
16..
17.解:在Rt△ACD中,CD=6,tanA=,
∴==,即AD=4.
又AB=12,
∴BD=AB-AD=8.
在Rt△BCD中,BC==10.
∴sinB===,cosB===.
∴sinB+cosB=+=.
18.解:∵四边形ABCD是矩形,
∴AB=CD,∠D=90°.
∵=,且由折叠知CF=BC,
∴=.
设CD=2x,CF=3x(x>0),
∴DF==x.
∴tan∠DCF===.
19.(1)cot30°=;
(2)解:∵tanA=,且tanA=,
∴设BC=3x,AC=4x.
∴cotA===.
第3课时 特殊角的三角函数值
1.A
2.A
3.B
4.2.
5.(1)sin30°+cos45°;
解:原式=+=.
(2)cos30°·tan30°-tan245°;
解:原式=×-12=-1=-.
(3)sin45°+sin60°·cos45°.
解:原式=×+×=.
6.D
7.C
8. 30°.
9. 60°.
10.B
11.D
12.解:sinA=sin18°36′≈0.319 0,
cosA=cos18°36′≈0.947 8,
tanA=tan18°36′≈0.336 5.
13.(1)sinα=0.822 1;
解:α≈55.3°.
(2)cosβ=0.843 4.
解:β≈32.5°.
14.B
15.D
16.D
17.C
18. .
19.(1)2 0180+(-1)2-2tan45°+;
解:原式=1+1-2×1+2
=2.
(2)(-1)-2+|-|+(π-3.14)0-tan60°+.
解:原式=1+(-)+1-+2
=2+.
20.解:解方程x2-(1+)x+=0,
得x1=1,x2=.
由题意知tanA=1或tanA=.
∴∠A=45°或60°.
21.解:(1)∵AB=AC=1,BC=,
∴AB2+AC2=BC2.
∴∠BAC=90°,∠B=∠C=45°.
(2)过点A作AD⊥BC,垂足为D.
∵AB=AC=1,AD⊥BC,
∴BD=BC=.
∴cosB===.
∴∠B=30°.
∴∠C=30°,∠BAC=120°.
22..
