5.2.2《 平行线的判定》同步练习 (含答案)
文档属性
| 名称 | 5.2.2《 平行线的判定》同步练习 (含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 89.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 19:34:55 | ||
图片预览


文档简介
人教版数学七下5.2.2《 平行线的判定》同步练习
一、选择题
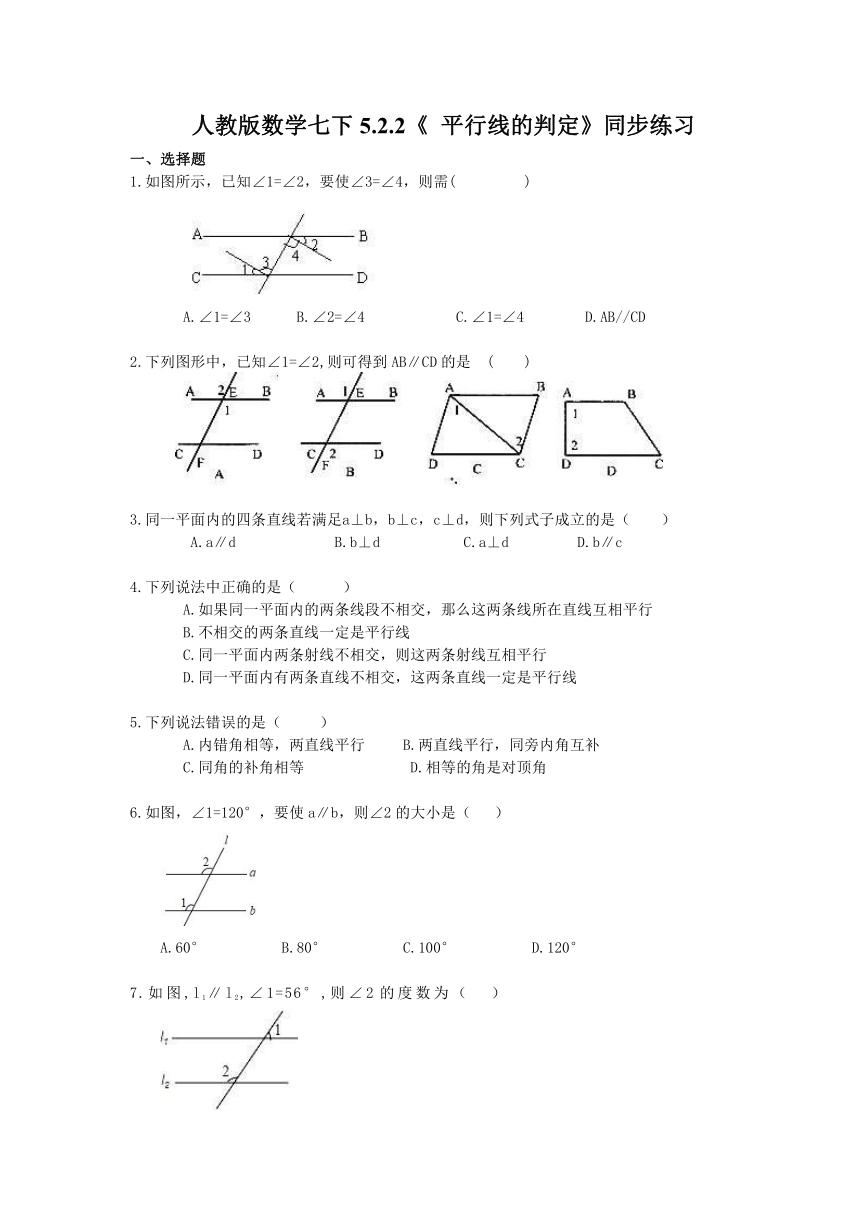
1.如图所示,已知∠1=∠2,要使∠3=∠4,则需( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠4 D.AB//CD
2.下列图形中,已知∠1=∠2,则可得到AB∥CD的是 ( )
3.同一平面内的四条直线若满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A.a∥d B.b⊥d C.a⊥d D.b∥c
4.下列说法中正确的是( )
A.如果同一平面内的两条线段不相交,那么这两条线所在直线互相平行
B.不相交的两条直线一定是平行线
C.同一平面内两条射线不相交,则这两条射线互相平行
D.同一平面内有两条直线不相交,这两条直线一定是平行线
5.下列说法错误的是( )
A.内错角相等,两直线平行 B.两直线平行,同旁内角互补
C.同角的补角相等 D.相等的角是对顶角
6.如图,∠1=120°,要使a∥b,则∠2的大小是( )
A.60° B.80° C.100° D.120°
7.如图,l1∥l2,∠1=56°,则∠2的度数为( )
A.34° B.56° C.124° D.146°
8.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠3=∠4 D.∠1=∠2
9.如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B+∠BDC=180°
10.如图,直线a、b被直线c所截,互为同旁内角的是( )
A.∠4和∠6 B.∠2和∠7 C.∠4和∠5 D.∠4和∠6
11.如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
A.50° B.60° C.120° D.130°
12.如图,在△ABC中,D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的 ( )
A.∠1=∠2 B.∠2=∠AFD C.∠1=∠AFD D.∠1=∠DFE
二、填空题
13.如图,若∠1=∠2,则 ∥ ,依据是 .
14.看图填理由:
∵直线AB,CD相交于O,(已知)
∴∠1与∠2是对顶角
∴∠1=∠2(___________________)
∵∠3+∠4=180°(已知)
∠1+∠4=180°(__________________)
∴∠1=∠3(__________________)
∴CD//AB(__________________)
15.长方形ABCD中,∠ADB=20°,现将这一长方形纸片沿AF折叠,若使AB′∥BD,则折痕AF与AB的夹角∠BAF应为_______.
16.如图,a∥b∥c,∠1=105°,∠2=140°,则∠α=________.
17.如图,已知∠ADE=46°,DF平分∠ADE,∠1=23°.求证:DF∥BE.
请你根据已知条件补充推理过程,并在相应括号内注明理由.
证明:∵DF平分∠ADE(已知)
∴ =∠ADE( )
又∵∠ADE=46°(已知),
∴ ∠ =23°,而∠1=23°(已知).
∴ ∥ ( )
18.如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是 .(填序号)
能够得到AB∥CD的条件是 .(填序号)
三、解答题
19.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
20.如图,已知∠1=250,∠2=450, ∠3=300,∠4=100.求证:AB//CD.
参考答案
D
B
C
D
D
答案为:D;
C
C
A
答案为:C.
答案为:B.
答案为:D.
答案为:AD,BC
答案为:对顶角相等;平角定义;同角的补角相等;同位角相等,两直线平行.
答案为:55° .
答案为:65°;
答案为:∠FDE;角平分线定义;∠FDE;DF;BE;内错角相等,两直线平行.
答案为:①④,②③⑤.
解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°,
又∵DE∥CF,∠CDE=130°,∴∠DCF+∠CDE=180°,∴∠DCF=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.
证明:如图.过点E作射线EM.使∠BEM=∠1=250,
∴AB//EM(内错角相等,两直线平行).
又∠2=450,
∴∠FEM= ∠2-∠BE=200.
过点F作射线FN,使∠EFN=200
∴∠EFN=∠FEM.
∴ EM//NF(内错角相等.两直线平行)
∵AB//NR ∠3=300
∴∠NFC=∠3-∠EFM=100.
又∠4=100, ∠4=∠NFC.
∴ CD//NF(内错角相等.两直线平行)
∴AB//CD.
一、选择题
1.如图所示,已知∠1=∠2,要使∠3=∠4,则需( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠4 D.AB//CD
2.下列图形中,已知∠1=∠2,则可得到AB∥CD的是 ( )
3.同一平面内的四条直线若满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A.a∥d B.b⊥d C.a⊥d D.b∥c
4.下列说法中正确的是( )
A.如果同一平面内的两条线段不相交,那么这两条线所在直线互相平行
B.不相交的两条直线一定是平行线
C.同一平面内两条射线不相交,则这两条射线互相平行
D.同一平面内有两条直线不相交,这两条直线一定是平行线
5.下列说法错误的是( )
A.内错角相等,两直线平行 B.两直线平行,同旁内角互补
C.同角的补角相等 D.相等的角是对顶角
6.如图,∠1=120°,要使a∥b,则∠2的大小是( )
A.60° B.80° C.100° D.120°
7.如图,l1∥l2,∠1=56°,则∠2的度数为( )
A.34° B.56° C.124° D.146°
8.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠3=∠4 D.∠1=∠2
9.如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B+∠BDC=180°
10.如图,直线a、b被直线c所截,互为同旁内角的是( )
A.∠4和∠6 B.∠2和∠7 C.∠4和∠5 D.∠4和∠6
11.如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
A.50° B.60° C.120° D.130°
12.如图,在△ABC中,D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的 ( )
A.∠1=∠2 B.∠2=∠AFD C.∠1=∠AFD D.∠1=∠DFE
二、填空题
13.如图,若∠1=∠2,则 ∥ ,依据是 .
14.看图填理由:
∵直线AB,CD相交于O,(已知)
∴∠1与∠2是对顶角
∴∠1=∠2(___________________)
∵∠3+∠4=180°(已知)
∠1+∠4=180°(__________________)
∴∠1=∠3(__________________)
∴CD//AB(__________________)
15.长方形ABCD中,∠ADB=20°,现将这一长方形纸片沿AF折叠,若使AB′∥BD,则折痕AF与AB的夹角∠BAF应为_______.
16.如图,a∥b∥c,∠1=105°,∠2=140°,则∠α=________.
17.如图,已知∠ADE=46°,DF平分∠ADE,∠1=23°.求证:DF∥BE.
请你根据已知条件补充推理过程,并在相应括号内注明理由.
证明:∵DF平分∠ADE(已知)
∴ =∠ADE( )
又∵∠ADE=46°(已知),
∴ ∠ =23°,而∠1=23°(已知).
∴ ∥ ( )
18.如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是 .(填序号)
能够得到AB∥CD的条件是 .(填序号)
三、解答题
19.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
20.如图,已知∠1=250,∠2=450, ∠3=300,∠4=100.求证:AB//CD.
参考答案
D
B
C
D
D
答案为:D;
C
C
A
答案为:C.
答案为:B.
答案为:D.
答案为:AD,BC
答案为:对顶角相等;平角定义;同角的补角相等;同位角相等,两直线平行.
答案为:55° .
答案为:65°;
答案为:∠FDE;角平分线定义;∠FDE;DF;BE;内错角相等,两直线平行.
答案为:①④,②③⑤.
解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°,
又∵DE∥CF,∠CDE=130°,∴∠DCF+∠CDE=180°,∴∠DCF=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.
证明:如图.过点E作射线EM.使∠BEM=∠1=250,
∴AB//EM(内错角相等,两直线平行).
又∠2=450,
∴∠FEM= ∠2-∠BE=200.
过点F作射线FN,使∠EFN=200
∴∠EFN=∠FEM.
∴ EM//NF(内错角相等.两直线平行)
∵AB//NR ∠3=300
∴∠NFC=∠3-∠EFM=100.
又∠4=100, ∠4=∠NFC.
∴ CD//NF(内错角相等.两直线平行)
∴AB//CD.
