27.1圆的确定 同步练习(含解析)
图片预览


文档简介
27.1圆的确定
同步练习
一.选择题(共10小题)
1.下列说法正确的是( )
A.长度相等的两条弧是等弧
B.三点确定一个圆
C.同一条弦所对的两条弧一定是等弧
D.半圆是弧
2.下列说法中,正确的是( )
A.同一条弦所对的两条弧一定是等弧
B.长度相等的两条弧是等弧
C.正多边形一定是轴对称图形
D.三角形的外心到三角形各边的距离相等
3.下列说法:(1)直径是弦;
(2)弦是直径;
(3)半圆是弧,但弧不一定是半圆;(4)半径相等的两个圆是等圆;
(5)长度相等的两条弧是等弧.
其中错误的个数是( )
A.1个
B.2个
C.3个
D.4个
4.点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
A.2
B.3
C.4
D.5
5.下列说法正确的是( )
A.顶点在圆内的角叫做圆心角
B.圆上任意两点间的部分叫做圆弧
C.由一条弧和经过这条弧的两个端点的两条线段组成的图形叫做扇形
D.在一个圆中,圆心角为1°的扇形的面积等于圆的面积的
6.到圆心的距离不大于半径的点的集合是( )
A.圆的外部
B.圆的内部
C.圆
D.圆的内部和圆
7.圆有( )条对称轴.
A.0
B.1
C.2
D.无数
8.已知线段AB长3厘米,经过A,B两点,以半径2厘米作圆,则( )
A.可作1个
B.可作2个
C.可作无数个
D.无法作出
9.下列四边形:①平行四边形;②矩形;③菱形;④正方形,其中四个顶点一定能在同一个圆上的有( )
A.①②③④
B.②③④
C.②④
D.③④
10.A、B是半径为5cm的⊙O上两个不同的点,则弦AB的取值范围是( )
A.AB>0
B.0<AB<5
C.0<AB<10
D.0<AB≤10
二.填空题(共5小题)
11.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都
,这个距离就是这个圆的
.
12.已知圆中最长的弦为6,则这个圆的半径为
.
13.平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3),
确定一个圆,(填“能”或“不能”).
14.战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于
.
15.如图,点
A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为
.
三.解答题(共2小题)
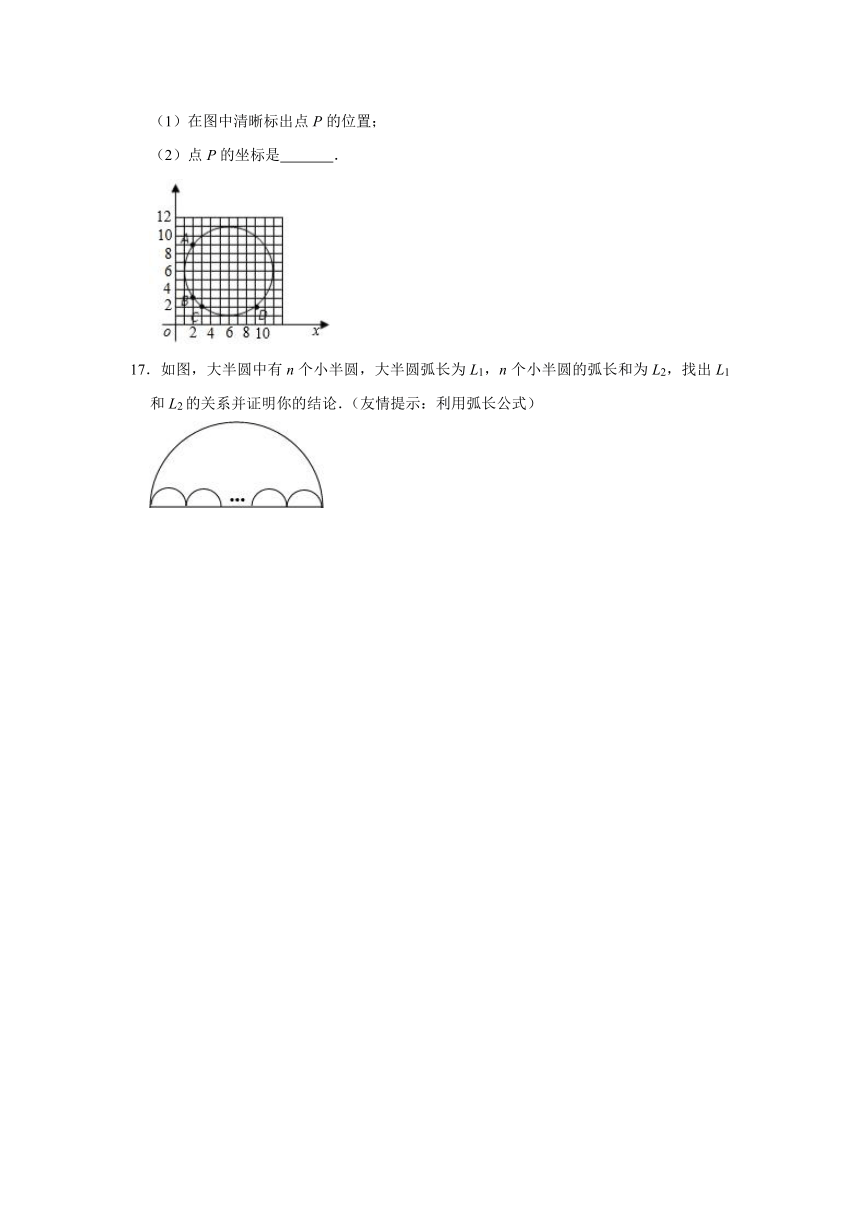
16.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是
.
17.如图,大半圆中有n个小半圆,大半圆弧长为L1,n个小半圆的弧长和为L2,找出L1和L2的关系并证明你的结论.(友情提示:利用弧长公式)
参考答案
1.解:A、长度相等的两条弧不一定是等弧,所以A选项错误;
B、不共线的三点确定一个圆,所以B选项错误;
C、同一条弦所对的两条弧不一定是等弧,所以C选项错误;
D、半圆是弧,所以D选项正确.
故选:D.
2.解:A、在同圆或等圆中,同一条弦所对的两条弧可能有一条是劣弧,一条是优弧,所以A选项错误;
B、在同圆或等圆中,长度相等的两条弧是等弧,所以B选项错误;
C、正多边形一定是轴对称图形,对称轴的条数等于它的边数,所以C选项正确;
D、三角形的外心到三角形三个顶点的距离相等,所以D选项错误.
故选:C.
3.解:(1)根据弦的概念,直径是一条线段,且两个端点在圆上,满足弦是连接圆上两点的线段这一概念,所以(1)正确;
(2)弦是连接圆上两点的线段,只有过圆心的弦才是直径,其它的弦不是直径,所以(2)错误;
(3)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆.所以(3)正确;
(4)由等圆的定义可知,半径相等的两个圆面积相等、周长相等,所以为等圆,所以(4)正确;
(5)等弧是能完全重合的弧,只有长度相等的两条弧不一定能重合.所以(5)错误.
故选:B.
4.解:由图可知,点A、B、E、C是⊙O上的点,
图中的弦有AB、BC、CE,一共3条.
故选:B.
5.解:A、错误.顶点在圆心的角叫做圆心角;
B、正确;
C、错误.由一条弧和经过这条弧的两个端点的两条线段组成的图形叫做弓形;
D、错误.在一个圆中,圆心角为1°的扇形的面积等于圆的面积的;、
故选:B.
6.解:根据点和圆的位置关系,知圆的内部是到圆心的距离小于的所有点的集合;
圆是到圆心的距离等于半径的所有点的集合.
所以与圆心的距离不大于半径的点所组成的图形是圆的内部(包括边界).
故选:D.
7.解:圆的对称轴是经过圆心的直线,经过一点的直线有无数条,
所以,圆有无数条对称轴.
故选:D.
8.解:如图,
分别以A、B为圆心、2cm为半径作圆,两圆相交于点C、D,
然后分别以C、D为圆心,2cm为半径作圆,则⊙C和⊙D为所求.
故选:B.
9.解:平行四边形、菱形的对角不一定互补,不一定能够四个点共圆;矩形、正方形的对角互补,四点一定共圆.
故选:C.
10.解:∵圆中最长的弦为直径,
∴0<AB≤10.
故选:D.
11.解:参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都相等,这个距离就是这个圆的半径.
故答案为:相等,半径.
12.解:∵圆中最长的弦为6,
∴⊙O的直径为6,
∴圆的半径为3.
故答案为:3.
13.解:∵B(0,﹣3)、C(2,﹣3),
∴BC∥x轴,
而点A(1,﹣3)与C、B共线,
∴点A、B、C共线,
∴三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3)不能确定一个圆.
故答案为:不能.
14.解:战国时期的《墨经》一书中记载:“圜(圆),一中同长也”.表示圆心到圆上各点的距离都相等,即半径都相等;
故答案为:半径.
15.解:如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为:5.
16.解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,
因而交点P的坐标是(6,6).
17.解:L1=L2.理由如下:
设n个小半圆半径依次为r1,r2,…,rn.
则大圆半径为(r1+r2+…+rn)
∴L1=π(r1+r2+…+rn),
L2=πr1+πr2+…+πrn
=π(r1+r2+…+rn),
∴L1=L2.
同步练习
一.选择题(共10小题)
1.下列说法正确的是( )
A.长度相等的两条弧是等弧
B.三点确定一个圆
C.同一条弦所对的两条弧一定是等弧
D.半圆是弧
2.下列说法中,正确的是( )
A.同一条弦所对的两条弧一定是等弧
B.长度相等的两条弧是等弧
C.正多边形一定是轴对称图形
D.三角形的外心到三角形各边的距离相等
3.下列说法:(1)直径是弦;
(2)弦是直径;
(3)半圆是弧,但弧不一定是半圆;(4)半径相等的两个圆是等圆;
(5)长度相等的两条弧是等弧.
其中错误的个数是( )
A.1个
B.2个
C.3个
D.4个
4.点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
A.2
B.3
C.4
D.5
5.下列说法正确的是( )
A.顶点在圆内的角叫做圆心角
B.圆上任意两点间的部分叫做圆弧
C.由一条弧和经过这条弧的两个端点的两条线段组成的图形叫做扇形
D.在一个圆中,圆心角为1°的扇形的面积等于圆的面积的
6.到圆心的距离不大于半径的点的集合是( )
A.圆的外部
B.圆的内部
C.圆
D.圆的内部和圆
7.圆有( )条对称轴.
A.0
B.1
C.2
D.无数
8.已知线段AB长3厘米,经过A,B两点,以半径2厘米作圆,则( )
A.可作1个
B.可作2个
C.可作无数个
D.无法作出
9.下列四边形:①平行四边形;②矩形;③菱形;④正方形,其中四个顶点一定能在同一个圆上的有( )
A.①②③④
B.②③④
C.②④
D.③④
10.A、B是半径为5cm的⊙O上两个不同的点,则弦AB的取值范围是( )
A.AB>0
B.0<AB<5
C.0<AB<10
D.0<AB≤10
二.填空题(共5小题)
11.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都
,这个距离就是这个圆的
.
12.已知圆中最长的弦为6,则这个圆的半径为
.
13.平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3),
确定一个圆,(填“能”或“不能”).
14.战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于
.
15.如图,点
A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为
.
三.解答题(共2小题)
16.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是
.
17.如图,大半圆中有n个小半圆,大半圆弧长为L1,n个小半圆的弧长和为L2,找出L1和L2的关系并证明你的结论.(友情提示:利用弧长公式)
参考答案
1.解:A、长度相等的两条弧不一定是等弧,所以A选项错误;
B、不共线的三点确定一个圆,所以B选项错误;
C、同一条弦所对的两条弧不一定是等弧,所以C选项错误;
D、半圆是弧,所以D选项正确.
故选:D.
2.解:A、在同圆或等圆中,同一条弦所对的两条弧可能有一条是劣弧,一条是优弧,所以A选项错误;
B、在同圆或等圆中,长度相等的两条弧是等弧,所以B选项错误;
C、正多边形一定是轴对称图形,对称轴的条数等于它的边数,所以C选项正确;
D、三角形的外心到三角形三个顶点的距离相等,所以D选项错误.
故选:C.
3.解:(1)根据弦的概念,直径是一条线段,且两个端点在圆上,满足弦是连接圆上两点的线段这一概念,所以(1)正确;
(2)弦是连接圆上两点的线段,只有过圆心的弦才是直径,其它的弦不是直径,所以(2)错误;
(3)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆.所以(3)正确;
(4)由等圆的定义可知,半径相等的两个圆面积相等、周长相等,所以为等圆,所以(4)正确;
(5)等弧是能完全重合的弧,只有长度相等的两条弧不一定能重合.所以(5)错误.
故选:B.
4.解:由图可知,点A、B、E、C是⊙O上的点,
图中的弦有AB、BC、CE,一共3条.
故选:B.
5.解:A、错误.顶点在圆心的角叫做圆心角;
B、正确;
C、错误.由一条弧和经过这条弧的两个端点的两条线段组成的图形叫做弓形;
D、错误.在一个圆中,圆心角为1°的扇形的面积等于圆的面积的;、
故选:B.
6.解:根据点和圆的位置关系,知圆的内部是到圆心的距离小于的所有点的集合;
圆是到圆心的距离等于半径的所有点的集合.
所以与圆心的距离不大于半径的点所组成的图形是圆的内部(包括边界).
故选:D.
7.解:圆的对称轴是经过圆心的直线,经过一点的直线有无数条,
所以,圆有无数条对称轴.
故选:D.
8.解:如图,
分别以A、B为圆心、2cm为半径作圆,两圆相交于点C、D,
然后分别以C、D为圆心,2cm为半径作圆,则⊙C和⊙D为所求.
故选:B.
9.解:平行四边形、菱形的对角不一定互补,不一定能够四个点共圆;矩形、正方形的对角互补,四点一定共圆.
故选:C.
10.解:∵圆中最长的弦为直径,
∴0<AB≤10.
故选:D.
11.解:参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都相等,这个距离就是这个圆的半径.
故答案为:相等,半径.
12.解:∵圆中最长的弦为6,
∴⊙O的直径为6,
∴圆的半径为3.
故答案为:3.
13.解:∵B(0,﹣3)、C(2,﹣3),
∴BC∥x轴,
而点A(1,﹣3)与C、B共线,
∴点A、B、C共线,
∴三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3)不能确定一个圆.
故答案为:不能.
14.解:战国时期的《墨经》一书中记载:“圜(圆),一中同长也”.表示圆心到圆上各点的距离都相等,即半径都相等;
故答案为:半径.
15.解:如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为:5.
16.解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,
因而交点P的坐标是(6,6).
17.解:L1=L2.理由如下:
设n个小半圆半径依次为r1,r2,…,rn.
则大圆半径为(r1+r2+…+rn)
∴L1=π(r1+r2+…+rn),
L2=πr1+πr2+…+πrn
=π(r1+r2+…+rn),
∴L1=L2.
