冀教版八年级数学上册 期末复习综合测试卷(含答案)
文档属性
| 名称 | 冀教版八年级数学上册 期末复习综合测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 223.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 20:34:05 | ||
图片预览



文档简介
冀教版八年级数学上册
期末复习综合测试卷
(时间:120分钟 满分:120分)
卷Ⅰ(选择题,共42分)
一、选择题(本大题共16个小题,1~10小题,每小题3分;11~16小题,每小题2分,共42分.每小题的四个选项中只有一个是正确的)
1.若在实数范围内有意义,则x的取值范围是(
)
A.x≤2
B.x≥-2
C.x<-2
D.x>-2
2.下列图案中是中心对称图形但不是轴对称图形的是(
)
3.在x+,,,-+z,,中,分式有(
)
A.1个
B.2个
C.3个
D.4个
4.若a<0,则|a-3|-的值为(
)
A.3
B.-3
C.3-2a
D.2a-3
5.下列各命题的逆命题是真命题的是(
)
A.对顶角相等
B.全等三角形的对应角相等
C.相等的角是同位角
D.等边三角形的三个内角都相等
6.如图,已知A,D,B,E在同一条直线上,且AD=BE,AC=DF,补充下列选项中一个条件后,不一定能得到△ABC≌△DEF的是(
)
A.BC=EF
B.∠C=∠F
C.AC∥DF
D.∠BAC=∠EDF
7.使分式的值等于0的x的值是(
)
A.-1
B.5
C.-1或5
D.1或-5
8.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是(
)
A.=
B.=
C.=
D.=
9.满足下列条件的是直角三角形的是(
)
A.BC=4,AC=5,AB=6
B.BC=,AC=,AB=
C.BC∶AC∶AB=3∶4∶5
D.∠A∶∠B∶∠C=3∶4∶5
10.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,△ABC的周长为19,△ACE的周长为13,则AB的长为(
)
A.3
B.6
C.12
D.16
11.实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是(
)
A.|a|>|b|
B.|b-d|=|b|+|d|
C.|a-c|=c-a
D.|d-1|>|c-a|
12.若关于x的方程-=0无解,则m的值是(
)
A.2
B.0
C.1
D.-2
13.如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为(
)
A.8
B.7
C.6
D.5
14.若等腰三角形的一个角比另一个角的2倍少20度,则等腰三角形顶角的度数是(
)
A.140°
B.20°或80°
C.44°或80°
D.140°或44°或80°
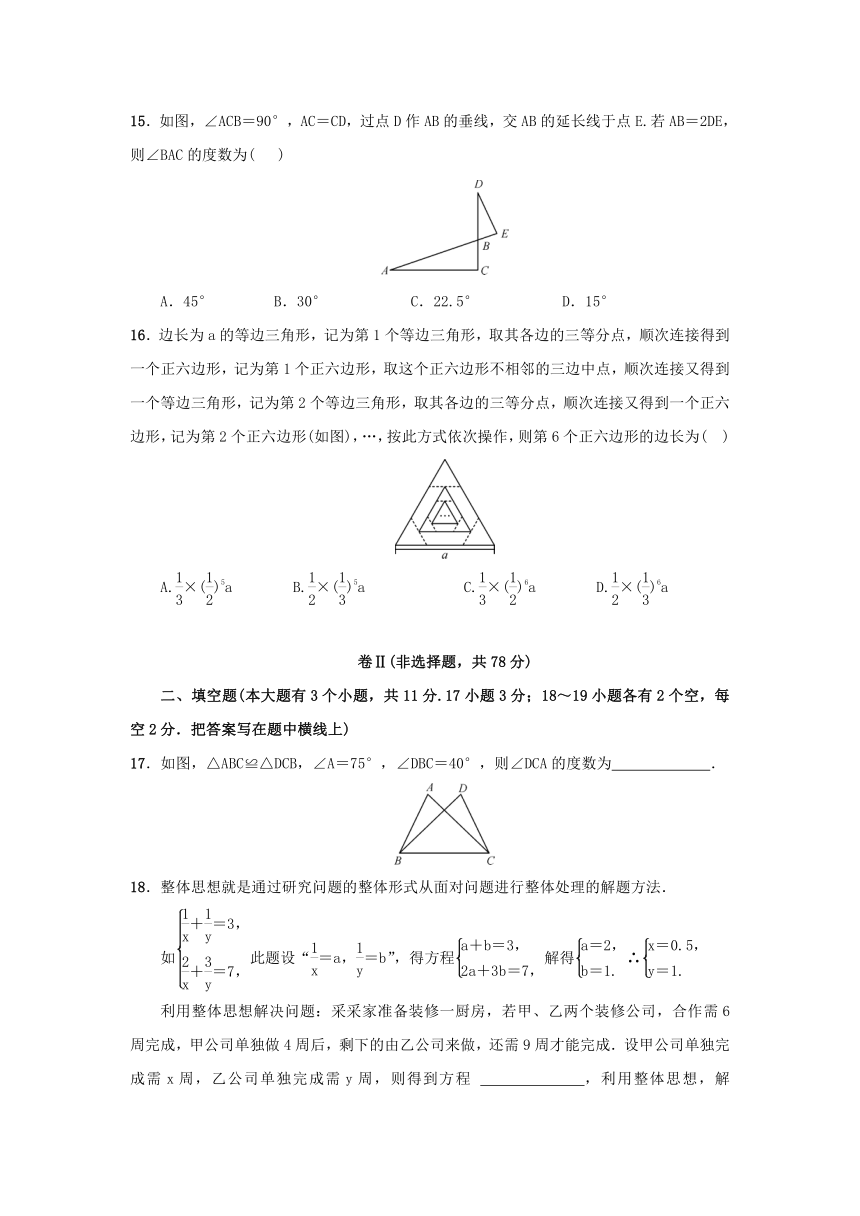
15.如图,∠ACB=90°,AC=CD,过点D作AB的垂线,交AB的延长线于点E.若AB=2DE,则∠BAC的度数为(
)
A.45°
B.30°
C.22.5°
D.15°
16.边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为(
)
A.×()5a
B.×()5a
C.×()6a
D.×()6a
卷Ⅱ(非选择题,共78分)
二、填空题(本大题有3个小题,共11分.17小题3分;18~19小题各有2个空,每空2分.把答案写在题中横线上)
17.如图,△ABC≌△DCB,∠A=75°,∠DBC=40°,则∠DCA的度数为
.
18.整体思想就是通过研究问题的整体形式从面对问题进行整体处理的解题方法.
如此题设“=a,=b”,得方程解得∴
利用整体思想解决问题:采采家准备装修一厨房,若甲、乙两个装修公司,合作需6周完成,甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成.设甲公司单独完成需x周,乙公司单独完成需y周,则得到方程
,利用整体思想,解得
.
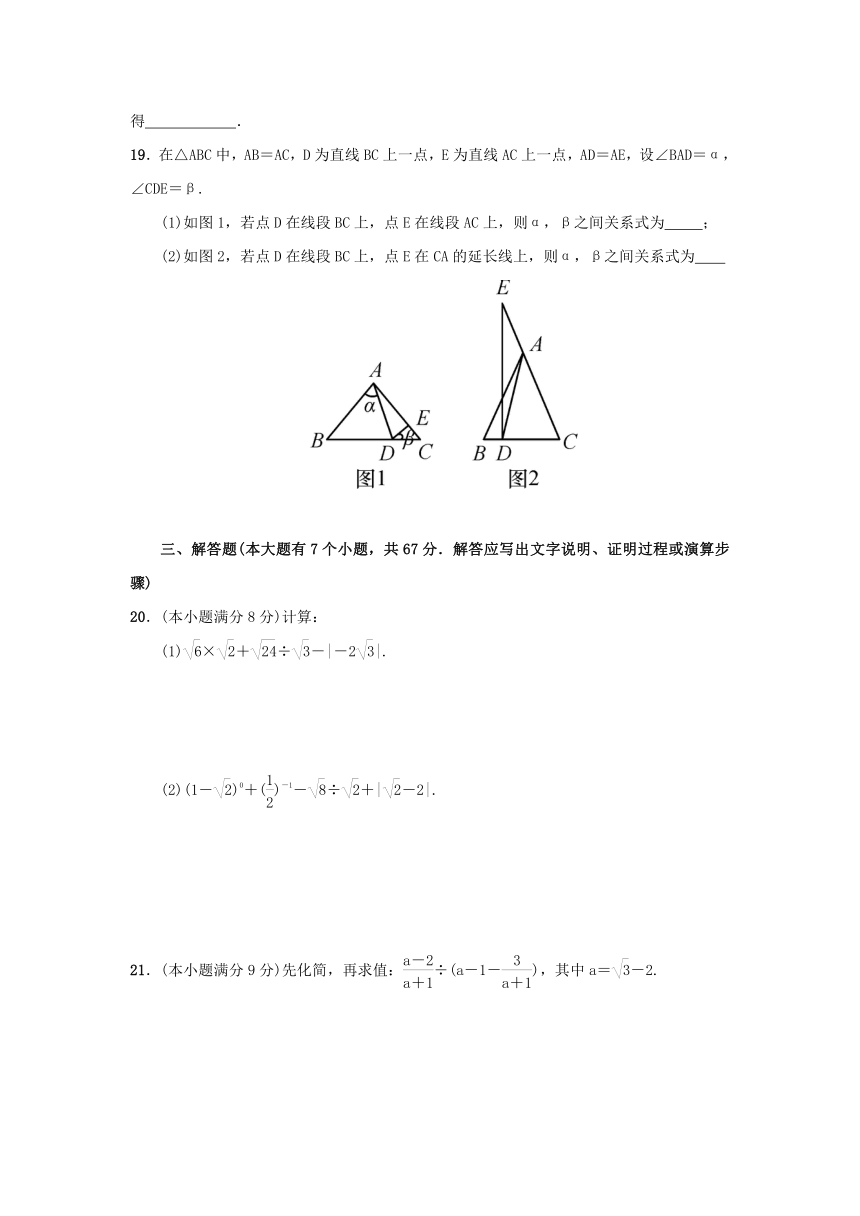
19.在△ABC中,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图1,若点D在线段BC上,点E在线段AC上,则α,β之间关系式为
;
(2)如图2,若点D在线段BC上,点E在CA的延长线上,则α,β之间关系式为
三、解答题(本大题有7个小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)计算:
(1)×+÷-|-2|.
(2)(1-)0+()-1-÷+|-2|.
21.(本小题满分9分)先化简,再求值:÷(a-1-),其中a=-2.
22.(本小题满分9分)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线作出△ABC与△DEF的对称轴l.
(2)结合所画图形,在直线l上画出点P,使PA+PC最小.
(3)如果每一个小正方形的边长为1,请直接写出△ABC的面积等于3.
23.(本小题满分9分)某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍;如果由甲、乙两队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成,则甲、乙两队合作完成该工程需要多少天?
24.(本小题满分10分)观察下列一组等式,然后解答后面的问题.
(+1)(-1)=1,
(+)(-)=1,
(+)(-)=1,
(+)(-)=1.
(1)观察以上规律,请写出第n个等式:
(n为正整数).
(2)利用上面的规律,计算++…+的值.
(3)利用上面的规律,比较-与-的大小.
25.(本小题满分10分)如图,在△ABC中,边AB,AC的垂直平分线分别交BC于点D,E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAD+∠CAE=60°,求∠BAC的度数.
26.(本小题满分12分)如图,在△ABC中,AB=AC,以BC为直角边作等腰Rt△BCD,∠CBD=90°,斜边CD交AB于点E.
(1)如图1,若∠ABC=60°,BE=4,作EH⊥BC于点H,求线段BC的长.
(2)如图2,作CF⊥AC,CF=AC,连接BF,且E为AB中点,求证:CD=2BF.
答案
(时间:120分钟 满分:120分)
卷Ⅰ(选择题,共42分)
一、选择题(本大题共16个小题,1~10小题,每小题3分;11~16小题,每小题2分,共42分.每小题的四个选项中只有一个是正确的)
1.若在实数范围内有意义,则x的取值范围是(
B
)
A.x≤2
B.x≥-2
C.x<-2
D.x>-2
2.下列图案中是中心对称图形但不是轴对称图形的是(
C
)
3.在x+,,,-+z,,中,分式有(
D
)
A.1个
B.2个
C.3个
D.4个
4.若a<0,则|a-3|-的值为(
A
)
A.3
B.-3
C.3-2a
D.2a-3
5.下列各命题的逆命题是真命题的是(
D
)
A.对顶角相等
B.全等三角形的对应角相等
C.相等的角是同位角
D.等边三角形的三个内角都相等
6.如图,已知A,D,B,E在同一条直线上,且AD=BE,AC=DF,补充下列选项中一个条件后,不一定能得到△ABC≌△DEF的是(
B
)
A.BC=EF
B.∠C=∠F
C.AC∥DF
D.∠BAC=∠EDF
7.使分式的值等于0的x的值是(
B
)
A.-1
B.5
C.-1或5
D.1或-5
8.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是(
C
)
A.=
B.=
C.=
D.=
9.满足下列条件的是直角三角形的是(
C
)
A.BC=4,AC=5,AB=6
B.BC=,AC=,AB=
C.BC∶AC∶AB=3∶4∶5
D.∠A∶∠B∶∠C=3∶4∶5
10.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,△ABC的周长为19,△ACE的周长为13,则AB的长为(
B
)
A.3
B.6
C.12
D.16
11.实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是(
D
)
A.|a|>|b|
B.|b-d|=|b|+|d|
C.|a-c|=c-a
D.|d-1|>|c-a|
12.若关于x的方程-=0无解,则m的值是(
A
)
A.2
B.0
C.1
D.-2
13.如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为(
C
)
A.8
B.7
C.6
D.5
14.若等腰三角形的一个角比另一个角的2倍少20度,则等腰三角形顶角的度数是(
D
)
A.140°
B.20°或80°
C.44°或80°
D.140°或44°或80°
15.如图,∠ACB=90°,AC=CD,过点D作AB的垂线,交AB的延长线于点E.若AB=2DE,则∠BAC的度数为(
C
)
A.45°
B.30°
C.22.5°
D.15°
16.边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为(
A
)
A.×()5a
B.×()5a
C.×()6a
D.×()6a
卷Ⅱ(非选择题,共78分)
二、填空题(本大题有3个小题,共11分.17小题3分;18~19小题各有2个空,每空2分.把答案写在题中横线上)
17.如图,△ABC≌△DCB,∠A=75°,∠DBC=40°,则∠DCA的度数为25°.
18.整体思想就是通过研究问题的整体形式从面对问题进行整体处理的解题方法.
如此题设“=a,=b”,得方程解得∴
利用整体思想解决问题:采采家准备装修一厨房,若甲、乙两个装修公司,合作需6周完成,甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成.设甲公司单独完成需x周,乙公司单独完成需y周,则得到方程,利用整体思想,解得.
19.在△ABC中,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图1,若点D在线段BC上,点E在线段AC上,则α,β之间关系式为a=2β;
(2)如图2,若点D在线段BC上,点E在CA的延长线上,则α,β之间关系式为α=2β-180°.
三、解答题(本大题有7个小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)计算:
(1)×+÷-|-2|.
解:原式=+-2=2+2-2=2.
(2)(1-)0+()-1-÷+|-2|.
解:原式=1+2-2+2-=3-.
21.(本小题满分9分)先化简,再求值:÷(a-1-),其中a=-2.
解:原式=÷=÷=·=.
当a=-2时,原式==.
22.(本小题满分9分)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线作出△ABC与△DEF的对称轴l.
(2)结合所画图形,在直线l上画出点P,使PA+PC最小.
(3)如果每一个小正方形的边长为1,请直接写出△ABC的面积等于3.
解:(1)如图所示,直线l即为所求.
(2)如图所示,点P即为所求.
23.(本小题满分9分)某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍;如果由甲、乙两队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成,则甲、乙两队合作完成该工程需要多少天?
解:(1)设这项工程的规定时间是x天,则甲队单独施工需要x天完工,乙队单独施工需要1.5x天完工,依题意,得
+=1,解得x=30.
经检验:x=30是原方程的解,且符合题意.
答:这项工程的规定时间是30天.
(2)由(1)可知:甲队单独施工需要30天完工,乙队单独施工需要45天完工,则甲、乙两队合作完成所需天数为1÷(+)=18(天).
答:甲、乙两队合作完成该工程需要18天.
24.(本小题满分10分)观察下列一组等式,然后解答后面的问题.
(+1)(-1)=1,
(+)(-)=1,
(+)(-)=1,
(+)(-)=1.
(1)观察以上规律,请写出第n个等式:(+)(-)=1(n为正整数).
(2)利用上面的规律,计算++…+的值.
(3)利用上面的规律,比较-与-的大小.
解:(2)原式=-1+-+…+-=-1=10-1=9.
(3)-=,-=,
∵<,
∴->-.
25.(本小题满分10分)如图,在△ABC中,边AB,AC的垂直平分线分别交BC于点D,E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAD+∠CAE=60°,求∠BAC的度数.
解:(1)边AB,AC的垂直平分线分别交BC于点D,E,∴DA=DB,EA=EC.
∴△ADE的周长为AD+DE+AE=BD+DE+EC=BC=5.
(2)∵DA=DB,EA=EC.
∴∠DAB=∠B,∠EAC=∠C.
∴∠B+∠C=∠DAB+∠EAC=60°.∴∠BAC=180°-(∠B+∠C)=120°.
26.(本小题满分12分)如图,在△ABC中,AB=AC,以BC为直角边作等腰Rt△BCD,∠CBD=90°,斜边CD交AB于点E.
(1)如图1,若∠ABC=60°,BE=4,作EH⊥BC于点H,求线段BC的长.
(2)如图2,作CF⊥AC,CF=AC,连接BF,且E为AB中点,求证:CD=2BF.
解:(1)∵∠ABC=60°,EH⊥BC,
∴∠BEH=30°.∴BH=BE,EH=BH.∴BH=2,EH=2.
∵∠CBD=90°,BD=BC,∴∠ECH=45°.∴HC=EH=2.
∴BC=BH+CH=2+2.
(2)过点A作AM⊥BC,交DC于点N.
∵AB=AC,AM⊥BC,∴BM=MC=BC=DB.
∵∠DCB=45°,AM⊥BC,∴∠DCB=∠MNC=45°.∴MN=MC=DB.
∵AM∥DB,∴==,==1,∴CD=2CN,AN=BD=BC.
∵CF⊥AC,∠BCD=45°,∴∠ACD+∠BCF=45°,且∠ACD+∠MAC=45°,
∴∠BCF=∠MAC.∵AC=CF,BC=AN,∴△ACN≌△CFB(SAS).
∴BF=CN,∴CD=2BF.
期末复习综合测试卷
(时间:120分钟 满分:120分)
卷Ⅰ(选择题,共42分)
一、选择题(本大题共16个小题,1~10小题,每小题3分;11~16小题,每小题2分,共42分.每小题的四个选项中只有一个是正确的)
1.若在实数范围内有意义,则x的取值范围是(
)
A.x≤2
B.x≥-2
C.x<-2
D.x>-2
2.下列图案中是中心对称图形但不是轴对称图形的是(
)
3.在x+,,,-+z,,中,分式有(
)
A.1个
B.2个
C.3个
D.4个
4.若a<0,则|a-3|-的值为(
)
A.3
B.-3
C.3-2a
D.2a-3
5.下列各命题的逆命题是真命题的是(
)
A.对顶角相等
B.全等三角形的对应角相等
C.相等的角是同位角
D.等边三角形的三个内角都相等
6.如图,已知A,D,B,E在同一条直线上,且AD=BE,AC=DF,补充下列选项中一个条件后,不一定能得到△ABC≌△DEF的是(
)
A.BC=EF
B.∠C=∠F
C.AC∥DF
D.∠BAC=∠EDF
7.使分式的值等于0的x的值是(
)
A.-1
B.5
C.-1或5
D.1或-5
8.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是(
)
A.=
B.=
C.=
D.=
9.满足下列条件的是直角三角形的是(
)
A.BC=4,AC=5,AB=6
B.BC=,AC=,AB=
C.BC∶AC∶AB=3∶4∶5
D.∠A∶∠B∶∠C=3∶4∶5
10.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,△ABC的周长为19,△ACE的周长为13,则AB的长为(
)
A.3
B.6
C.12
D.16
11.实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是(
)
A.|a|>|b|
B.|b-d|=|b|+|d|
C.|a-c|=c-a
D.|d-1|>|c-a|
12.若关于x的方程-=0无解,则m的值是(
)
A.2
B.0
C.1
D.-2
13.如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为(
)
A.8
B.7
C.6
D.5
14.若等腰三角形的一个角比另一个角的2倍少20度,则等腰三角形顶角的度数是(
)
A.140°
B.20°或80°
C.44°或80°
D.140°或44°或80°
15.如图,∠ACB=90°,AC=CD,过点D作AB的垂线,交AB的延长线于点E.若AB=2DE,则∠BAC的度数为(
)
A.45°
B.30°
C.22.5°
D.15°
16.边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为(
)
A.×()5a
B.×()5a
C.×()6a
D.×()6a
卷Ⅱ(非选择题,共78分)
二、填空题(本大题有3个小题,共11分.17小题3分;18~19小题各有2个空,每空2分.把答案写在题中横线上)
17.如图,△ABC≌△DCB,∠A=75°,∠DBC=40°,则∠DCA的度数为
.
18.整体思想就是通过研究问题的整体形式从面对问题进行整体处理的解题方法.
如此题设“=a,=b”,得方程解得∴
利用整体思想解决问题:采采家准备装修一厨房,若甲、乙两个装修公司,合作需6周完成,甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成.设甲公司单独完成需x周,乙公司单独完成需y周,则得到方程
,利用整体思想,解得
.
19.在△ABC中,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图1,若点D在线段BC上,点E在线段AC上,则α,β之间关系式为
;
(2)如图2,若点D在线段BC上,点E在CA的延长线上,则α,β之间关系式为
三、解答题(本大题有7个小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)计算:
(1)×+÷-|-2|.
(2)(1-)0+()-1-÷+|-2|.
21.(本小题满分9分)先化简,再求值:÷(a-1-),其中a=-2.
22.(本小题满分9分)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线作出△ABC与△DEF的对称轴l.
(2)结合所画图形,在直线l上画出点P,使PA+PC最小.
(3)如果每一个小正方形的边长为1,请直接写出△ABC的面积等于3.
23.(本小题满分9分)某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍;如果由甲、乙两队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成,则甲、乙两队合作完成该工程需要多少天?
24.(本小题满分10分)观察下列一组等式,然后解答后面的问题.
(+1)(-1)=1,
(+)(-)=1,
(+)(-)=1,
(+)(-)=1.
(1)观察以上规律,请写出第n个等式:
(n为正整数).
(2)利用上面的规律,计算++…+的值.
(3)利用上面的规律,比较-与-的大小.
25.(本小题满分10分)如图,在△ABC中,边AB,AC的垂直平分线分别交BC于点D,E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAD+∠CAE=60°,求∠BAC的度数.
26.(本小题满分12分)如图,在△ABC中,AB=AC,以BC为直角边作等腰Rt△BCD,∠CBD=90°,斜边CD交AB于点E.
(1)如图1,若∠ABC=60°,BE=4,作EH⊥BC于点H,求线段BC的长.
(2)如图2,作CF⊥AC,CF=AC,连接BF,且E为AB中点,求证:CD=2BF.
答案
(时间:120分钟 满分:120分)
卷Ⅰ(选择题,共42分)
一、选择题(本大题共16个小题,1~10小题,每小题3分;11~16小题,每小题2分,共42分.每小题的四个选项中只有一个是正确的)
1.若在实数范围内有意义,则x的取值范围是(
B
)
A.x≤2
B.x≥-2
C.x<-2
D.x>-2
2.下列图案中是中心对称图形但不是轴对称图形的是(
C
)
3.在x+,,,-+z,,中,分式有(
D
)
A.1个
B.2个
C.3个
D.4个
4.若a<0,则|a-3|-的值为(
A
)
A.3
B.-3
C.3-2a
D.2a-3
5.下列各命题的逆命题是真命题的是(
D
)
A.对顶角相等
B.全等三角形的对应角相等
C.相等的角是同位角
D.等边三角形的三个内角都相等
6.如图,已知A,D,B,E在同一条直线上,且AD=BE,AC=DF,补充下列选项中一个条件后,不一定能得到△ABC≌△DEF的是(
B
)
A.BC=EF
B.∠C=∠F
C.AC∥DF
D.∠BAC=∠EDF
7.使分式的值等于0的x的值是(
B
)
A.-1
B.5
C.-1或5
D.1或-5
8.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是(
C
)
A.=
B.=
C.=
D.=
9.满足下列条件的是直角三角形的是(
C
)
A.BC=4,AC=5,AB=6
B.BC=,AC=,AB=
C.BC∶AC∶AB=3∶4∶5
D.∠A∶∠B∶∠C=3∶4∶5
10.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,△ABC的周长为19,△ACE的周长为13,则AB的长为(
B
)
A.3
B.6
C.12
D.16
11.实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是(
D
)
A.|a|>|b|
B.|b-d|=|b|+|d|
C.|a-c|=c-a
D.|d-1|>|c-a|
12.若关于x的方程-=0无解,则m的值是(
A
)
A.2
B.0
C.1
D.-2
13.如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为(
C
)
A.8
B.7
C.6
D.5
14.若等腰三角形的一个角比另一个角的2倍少20度,则等腰三角形顶角的度数是(
D
)
A.140°
B.20°或80°
C.44°或80°
D.140°或44°或80°
15.如图,∠ACB=90°,AC=CD,过点D作AB的垂线,交AB的延长线于点E.若AB=2DE,则∠BAC的度数为(
C
)
A.45°
B.30°
C.22.5°
D.15°
16.边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为(
A
)
A.×()5a
B.×()5a
C.×()6a
D.×()6a
卷Ⅱ(非选择题,共78分)
二、填空题(本大题有3个小题,共11分.17小题3分;18~19小题各有2个空,每空2分.把答案写在题中横线上)
17.如图,△ABC≌△DCB,∠A=75°,∠DBC=40°,则∠DCA的度数为25°.
18.整体思想就是通过研究问题的整体形式从面对问题进行整体处理的解题方法.
如此题设“=a,=b”,得方程解得∴
利用整体思想解决问题:采采家准备装修一厨房,若甲、乙两个装修公司,合作需6周完成,甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成.设甲公司单独完成需x周,乙公司单独完成需y周,则得到方程,利用整体思想,解得.
19.在△ABC中,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图1,若点D在线段BC上,点E在线段AC上,则α,β之间关系式为a=2β;
(2)如图2,若点D在线段BC上,点E在CA的延长线上,则α,β之间关系式为α=2β-180°.
三、解答题(本大题有7个小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)计算:
(1)×+÷-|-2|.
解:原式=+-2=2+2-2=2.
(2)(1-)0+()-1-÷+|-2|.
解:原式=1+2-2+2-=3-.
21.(本小题满分9分)先化简,再求值:÷(a-1-),其中a=-2.
解:原式=÷=÷=·=.
当a=-2时,原式==.
22.(本小题满分9分)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线作出△ABC与△DEF的对称轴l.
(2)结合所画图形,在直线l上画出点P,使PA+PC最小.
(3)如果每一个小正方形的边长为1,请直接写出△ABC的面积等于3.
解:(1)如图所示,直线l即为所求.
(2)如图所示,点P即为所求.
23.(本小题满分9分)某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍;如果由甲、乙两队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成,则甲、乙两队合作完成该工程需要多少天?
解:(1)设这项工程的规定时间是x天,则甲队单独施工需要x天完工,乙队单独施工需要1.5x天完工,依题意,得
+=1,解得x=30.
经检验:x=30是原方程的解,且符合题意.
答:这项工程的规定时间是30天.
(2)由(1)可知:甲队单独施工需要30天完工,乙队单独施工需要45天完工,则甲、乙两队合作完成所需天数为1÷(+)=18(天).
答:甲、乙两队合作完成该工程需要18天.
24.(本小题满分10分)观察下列一组等式,然后解答后面的问题.
(+1)(-1)=1,
(+)(-)=1,
(+)(-)=1,
(+)(-)=1.
(1)观察以上规律,请写出第n个等式:(+)(-)=1(n为正整数).
(2)利用上面的规律,计算++…+的值.
(3)利用上面的规律,比较-与-的大小.
解:(2)原式=-1+-+…+-=-1=10-1=9.
(3)-=,-=,
∵<,
∴->-.
25.(本小题满分10分)如图,在△ABC中,边AB,AC的垂直平分线分别交BC于点D,E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAD+∠CAE=60°,求∠BAC的度数.
解:(1)边AB,AC的垂直平分线分别交BC于点D,E,∴DA=DB,EA=EC.
∴△ADE的周长为AD+DE+AE=BD+DE+EC=BC=5.
(2)∵DA=DB,EA=EC.
∴∠DAB=∠B,∠EAC=∠C.
∴∠B+∠C=∠DAB+∠EAC=60°.∴∠BAC=180°-(∠B+∠C)=120°.
26.(本小题满分12分)如图,在△ABC中,AB=AC,以BC为直角边作等腰Rt△BCD,∠CBD=90°,斜边CD交AB于点E.
(1)如图1,若∠ABC=60°,BE=4,作EH⊥BC于点H,求线段BC的长.
(2)如图2,作CF⊥AC,CF=AC,连接BF,且E为AB中点,求证:CD=2BF.
解:(1)∵∠ABC=60°,EH⊥BC,
∴∠BEH=30°.∴BH=BE,EH=BH.∴BH=2,EH=2.
∵∠CBD=90°,BD=BC,∴∠ECH=45°.∴HC=EH=2.
∴BC=BH+CH=2+2.
(2)过点A作AM⊥BC,交DC于点N.
∵AB=AC,AM⊥BC,∴BM=MC=BC=DB.
∵∠DCB=45°,AM⊥BC,∴∠DCB=∠MNC=45°.∴MN=MC=DB.
∵AM∥DB,∴==,==1,∴CD=2CN,AN=BD=BC.
∵CF⊥AC,∠BCD=45°,∴∠ACD+∠BCF=45°,且∠ACD+∠MAC=45°,
∴∠BCF=∠MAC.∵AC=CF,BC=AN,∴△ACN≌△CFB(SAS).
∴BF=CN,∴CD=2BF.
同课章节目录
