苏科版八年级数学上册知识讲义-1.全等三角形简单辅助线的作法(含答案)
文档属性
| 名称 | 苏科版八年级数学上册知识讲义-1.全等三角形简单辅助线的作法(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 09:55:24 | ||
图片预览


文档简介
初中数学
简单辅助线的作法
精讲精练
【考点精讲】
常见辅助线的作法:
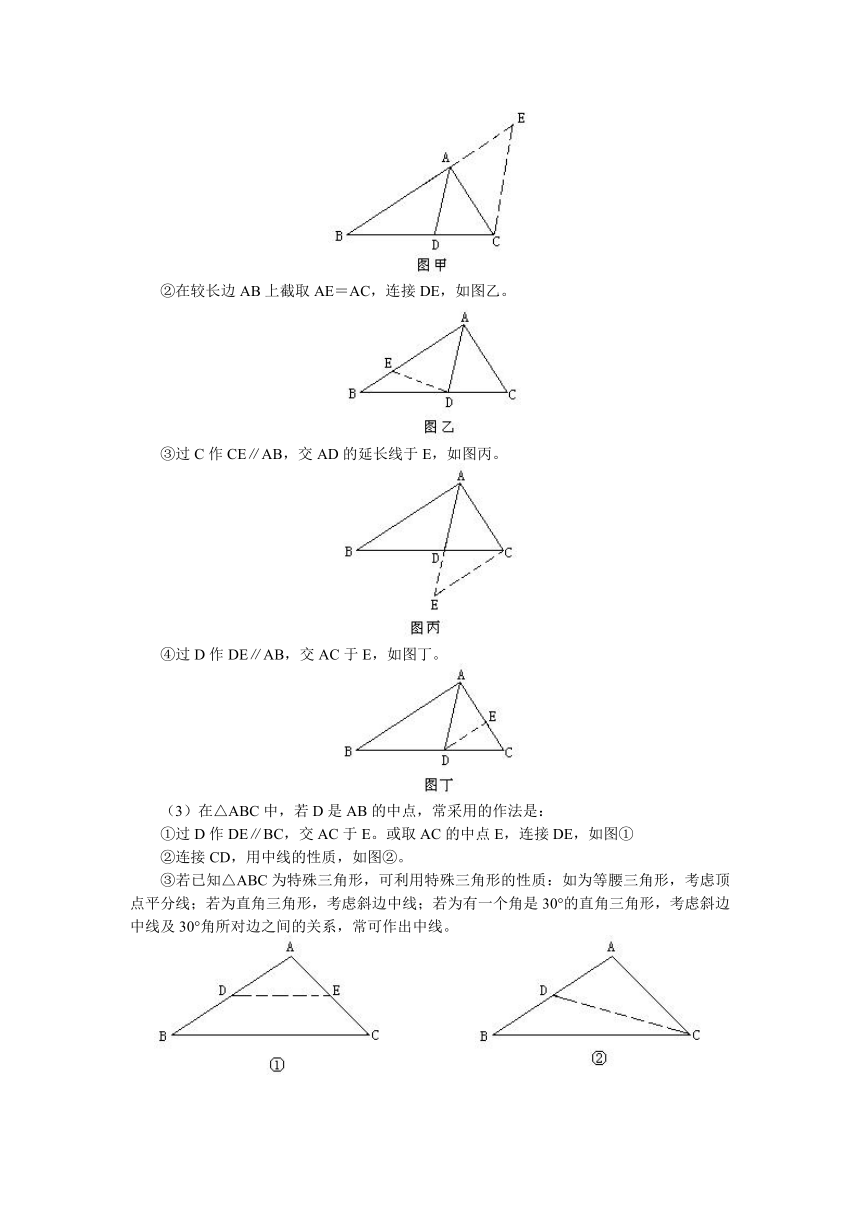
(1)在△ABC中,如果AD是中线,常采用的作法是:
①延长AD到E,使DE=AD,连接BE(或过B作BE∥AC,交AD的延长线于E),如图甲。
②取AC的中点E,连接DE(或过D作DE∥BA,交AC于E),如图乙。
③延长BA至E,使AE=AB,连接CE(或过C作CE∥AD交BA的延长线于E),如图丙。
(2)在△ABC中,若AD是∠BAC的平分线,常采用的作法是:
①延长BA至E,使AE=AC,连接CE(或过C作CE∥AD,交BA的延长线于E),如图甲。
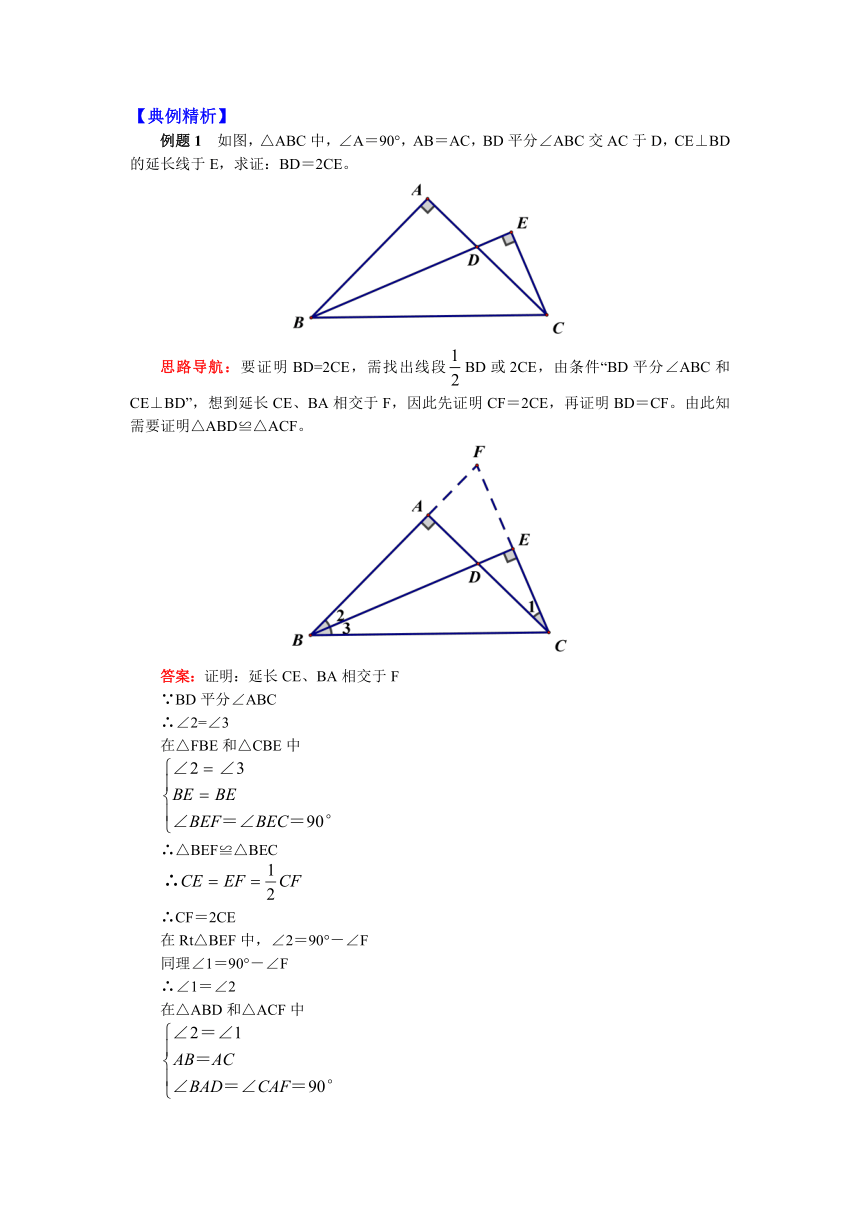
②在较长边AB上截取AE=AC,连接DE,如图乙。
③过C作CE∥AB,交AD的延长线于E,如图丙。
④过D作DE∥AB,交AC于E,如图丁。
(3)在△ABC中,若D是AB的中点,常采用的作法是:
①过D作DE∥BC,交AC于E。或取AC的中点E,连接DE,如图①
②连接CD,用中线的性质,如图②。
③若已知△ABC为特殊三角形,可利用特殊三角形的性质:如为等腰三角形,考虑顶点平分线;若为直角三角形,考虑斜边中线;若为有一个角是30°的直角三角形,考虑斜边中线及30°角所对边之间的关系,常可作出中线。
【典例精析】
例题1
如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABC交AC于D,CE⊥BD的延长线于E,求证:BD=2CE。
思路导航:要证明BD=2CE,需找出线段BD或2CE,由条件“BD平分∠ABC和CE⊥BD”,想到延长CE、BA相交于F,因此先证明CF=2CE,再证明BD=CF。由此知需要证明△ABD≌△ACF。
答案:证明:延长CE、BA相交于F
∵BD平分∠ABC
∴∠2=∠3
在△FBE和△CBE中
∴△BEF≌△BEC
∴CF=2CE
在Rt△BEF中,∠2=90°-∠F
同理∠1=90°-∠F
∴∠1=∠2
在△ABD和△ACF中
∴△ABD≌△ACF
∴BD=CF
∴BD=2CE
点评:①在题目中如果含有角平分线且含有和这条角平分线垂直的条件时,要想到翻折图形。此题所作的辅助线,实质上是将Rt△BCE以BE所在的直线为轴翻折过去得到Rt△BFE。
②此题图中,可以把BE、CA看成是△FBC的两条高,注意“∠1=∠2”这个结论。
例题2
如图,已知AC∥BD、EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗?请说明理由。
思路导航:问题是关于AB与AC+BD相等关系的,直接证明较为麻烦,且很难想到思路,所以还是要添加辅助线把题目简化些。通常会在AB上截取AF=AC,连接EF。
可先证明出△ACE≌△AFE,之后再证明出△EFB≌△EDB,由全等三角形对应边相等得出FB=DB,再加上AF=AC,就能得出结论AC+BD=AF+FB=AB。
答案:相等。
证法一:如图(1)在AB上截取AF=AC,连接EF。
在△ACE和△AFE中,
∵
∴△ACE≌△AFE(SAS)
∴∠5=∠C
∵AC∥BD
∴∠C+∠D=180°,
又∵∠5+∠6=180°
∴∠6=∠D
在△EFB和△EDB中,
∵
∴△EFB≌△EDB(AAS)
∴FB=DB
∴AC+BD=AF+FB=AB
证法二:如图(2),延长BE,与AC的延长线相交于点F
∵AC∥BD
∴∠F=∠4
又∵∠3=∠4
∴∠F=∠3
在△AEF和△AEB中,
∵
∴△AEF≌△AEB(AAS)
∴AB=AF,BE=FE
在△BED和△FEC中,
∵
∴△BED≌△FEC(ASA)
∴BD=FC
∴AB=AF=AC+CF=AC+BD。即AB=AC+BD得证
点评:对于结论是一条线段与另一条线段之和等于第三条线段这类题目,常采用截长法(或补短法)。所谓截长法就是把第三条线段分成两部分,证其中的一部分等于第一条线段,而另一部分等于第二条线段。
【总结提升】
三角形问题添加辅助线方法
1.
有关三角形中线的题目,常将中线加倍。含有中点的题目,常利用三角形的中位线。通过这种方法,可以把要证的结论恰当地转移,能很容易地解决问题。
2.
含有平分线的题目,常以角平分线为对称轴,利用角平分线的性质和题中的条件,构造出全等三角形,从而利用全等三角形的知识解决问题。
3.
结论是两线段相等的题目,常画辅助线构成全等三角形,或利用关于平分线的一些定理。
4.
结论是一条线段与另一条线段之和等于第三条线段这类题目,常采用截长法或补短法。
同步练习
(答题时间:20分钟)
一、填空题
1.
如图,已知,,,则等于
。
2.
如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E。
若PE=2,则两平行线AD与BC间的距离为
。
?
?
3.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP=_______________。
二、解答题
4.
已知:如图,在四边形ABCD中,AB=CB,AD=CD。
求证:∠C=∠A。
5.
如图,AD=BC,AB=DC。
求证:∠A+∠D=180°
答案
1.
23°
解析:连接AC,可知AB=CD(已知),AD=BC(已知),AC=CA(公共边),由SSS即可证出△ACB≌△CAD,所以∠D=∠B=23°。
2.
4
解析:过点P作PF⊥AD于点F,作PG⊥BC于点G,由角平分线的性质定理可知:PF=PE,PG=PE,即
PF=PG=PE=2,而两平行线AD与BC间的距离为PF+PG=4,故答案为4。
3.
50°
解析:由三角形外角等于与它不相邻的两个内角之和及等量代换可知,∠BAC=2∠BPC=2×40°=80°。(详见3期),如图所示:过点P作PE⊥BA延长线于E,PG⊥BC于点G,PF⊥AC于点F,由角平分线的性质可知:PG=PF,PG=PE,即:PF=PE,所以BP是∠EAC的平分线,所以∠CAP=∠EAC=(180°-∠BAC)=×(180°-80°)=50°。
4.
证明:连接BD,
∵AB=CB,AD=CD,BD=BD
∴△DAB≌△DCB
∴∠C=∠A
5.
证明:连接AC
∵AD=BC,AB=DC,AC=CA
∴△ABC≌△CDA
∴∠BAC=∠ACD
∴AB∥CD
∴∠A+∠D=180°
简单辅助线的作法
精讲精练
【考点精讲】
常见辅助线的作法:
(1)在△ABC中,如果AD是中线,常采用的作法是:
①延长AD到E,使DE=AD,连接BE(或过B作BE∥AC,交AD的延长线于E),如图甲。
②取AC的中点E,连接DE(或过D作DE∥BA,交AC于E),如图乙。
③延长BA至E,使AE=AB,连接CE(或过C作CE∥AD交BA的延长线于E),如图丙。
(2)在△ABC中,若AD是∠BAC的平分线,常采用的作法是:
①延长BA至E,使AE=AC,连接CE(或过C作CE∥AD,交BA的延长线于E),如图甲。
②在较长边AB上截取AE=AC,连接DE,如图乙。
③过C作CE∥AB,交AD的延长线于E,如图丙。
④过D作DE∥AB,交AC于E,如图丁。
(3)在△ABC中,若D是AB的中点,常采用的作法是:
①过D作DE∥BC,交AC于E。或取AC的中点E,连接DE,如图①
②连接CD,用中线的性质,如图②。
③若已知△ABC为特殊三角形,可利用特殊三角形的性质:如为等腰三角形,考虑顶点平分线;若为直角三角形,考虑斜边中线;若为有一个角是30°的直角三角形,考虑斜边中线及30°角所对边之间的关系,常可作出中线。
【典例精析】
例题1
如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABC交AC于D,CE⊥BD的延长线于E,求证:BD=2CE。
思路导航:要证明BD=2CE,需找出线段BD或2CE,由条件“BD平分∠ABC和CE⊥BD”,想到延长CE、BA相交于F,因此先证明CF=2CE,再证明BD=CF。由此知需要证明△ABD≌△ACF。
答案:证明:延长CE、BA相交于F
∵BD平分∠ABC
∴∠2=∠3
在△FBE和△CBE中
∴△BEF≌△BEC
∴CF=2CE
在Rt△BEF中,∠2=90°-∠F
同理∠1=90°-∠F
∴∠1=∠2
在△ABD和△ACF中
∴△ABD≌△ACF
∴BD=CF
∴BD=2CE
点评:①在题目中如果含有角平分线且含有和这条角平分线垂直的条件时,要想到翻折图形。此题所作的辅助线,实质上是将Rt△BCE以BE所在的直线为轴翻折过去得到Rt△BFE。
②此题图中,可以把BE、CA看成是△FBC的两条高,注意“∠1=∠2”这个结论。
例题2
如图,已知AC∥BD、EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗?请说明理由。
思路导航:问题是关于AB与AC+BD相等关系的,直接证明较为麻烦,且很难想到思路,所以还是要添加辅助线把题目简化些。通常会在AB上截取AF=AC,连接EF。
可先证明出△ACE≌△AFE,之后再证明出△EFB≌△EDB,由全等三角形对应边相等得出FB=DB,再加上AF=AC,就能得出结论AC+BD=AF+FB=AB。
答案:相等。
证法一:如图(1)在AB上截取AF=AC,连接EF。
在△ACE和△AFE中,
∵
∴△ACE≌△AFE(SAS)
∴∠5=∠C
∵AC∥BD
∴∠C+∠D=180°,
又∵∠5+∠6=180°
∴∠6=∠D
在△EFB和△EDB中,
∵
∴△EFB≌△EDB(AAS)
∴FB=DB
∴AC+BD=AF+FB=AB
证法二:如图(2),延长BE,与AC的延长线相交于点F
∵AC∥BD
∴∠F=∠4
又∵∠3=∠4
∴∠F=∠3
在△AEF和△AEB中,
∵
∴△AEF≌△AEB(AAS)
∴AB=AF,BE=FE
在△BED和△FEC中,
∵
∴△BED≌△FEC(ASA)
∴BD=FC
∴AB=AF=AC+CF=AC+BD。即AB=AC+BD得证
点评:对于结论是一条线段与另一条线段之和等于第三条线段这类题目,常采用截长法(或补短法)。所谓截长法就是把第三条线段分成两部分,证其中的一部分等于第一条线段,而另一部分等于第二条线段。
【总结提升】
三角形问题添加辅助线方法
1.
有关三角形中线的题目,常将中线加倍。含有中点的题目,常利用三角形的中位线。通过这种方法,可以把要证的结论恰当地转移,能很容易地解决问题。
2.
含有平分线的题目,常以角平分线为对称轴,利用角平分线的性质和题中的条件,构造出全等三角形,从而利用全等三角形的知识解决问题。
3.
结论是两线段相等的题目,常画辅助线构成全等三角形,或利用关于平分线的一些定理。
4.
结论是一条线段与另一条线段之和等于第三条线段这类题目,常采用截长法或补短法。
同步练习
(答题时间:20分钟)
一、填空题
1.
如图,已知,,,则等于
。
2.
如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E。
若PE=2,则两平行线AD与BC间的距离为
。
?
?
3.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP=_______________。
二、解答题
4.
已知:如图,在四边形ABCD中,AB=CB,AD=CD。
求证:∠C=∠A。
5.
如图,AD=BC,AB=DC。
求证:∠A+∠D=180°
答案
1.
23°
解析:连接AC,可知AB=CD(已知),AD=BC(已知),AC=CA(公共边),由SSS即可证出△ACB≌△CAD,所以∠D=∠B=23°。
2.
4
解析:过点P作PF⊥AD于点F,作PG⊥BC于点G,由角平分线的性质定理可知:PF=PE,PG=PE,即
PF=PG=PE=2,而两平行线AD与BC间的距离为PF+PG=4,故答案为4。
3.
50°
解析:由三角形外角等于与它不相邻的两个内角之和及等量代换可知,∠BAC=2∠BPC=2×40°=80°。(详见3期),如图所示:过点P作PE⊥BA延长线于E,PG⊥BC于点G,PF⊥AC于点F,由角平分线的性质可知:PG=PF,PG=PE,即:PF=PE,所以BP是∠EAC的平分线,所以∠CAP=∠EAC=(180°-∠BAC)=×(180°-80°)=50°。
4.
证明:连接BD,
∵AB=CB,AD=CD,BD=BD
∴△DAB≌△DCB
∴∠C=∠A
5.
证明:连接AC
∵AD=BC,AB=DC,AC=CA
∴△ABC≌△CDA
∴∠BAC=∠ACD
∴AB∥CD
∴∠A+∠D=180°
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
