1.2充分条件与必要条件-北师大版高中数学选修2-1课件(18张PPT)
文档属性
| 名称 | 1.2充分条件与必要条件-北师大版高中数学选修2-1课件(18张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 984.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览






文档简介
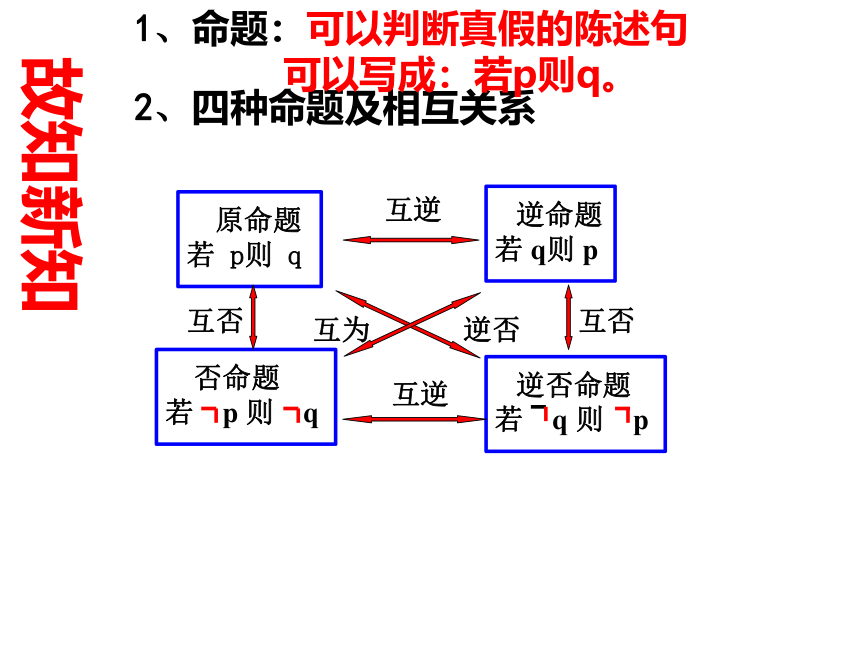
2、四种命题及相互关系
1、命题:可以判断真假的陈述句
可以写成:若p则q。
故知新知
原命题 若 p则 q
逆命题 若 q则 p
否命题 若 p 则 q
逆否命题若 q 则 p
互逆
互逆
互否
互否
互为
逆否
同学们,当某一天你和你妈妈在街上遇到老师的时候,你向老师介绍你的妈妈说:“这是我的妈妈”。那么大家想一想这个时候你的妈妈还会不会补充说:“这是我的孩子”呢?
不会了!为什么呢?
因为前面你所介绍的她是你的妈妈就足以保证你是她的 孩子。那么,这在数学中是一层什么样的关系呢?今天我们就来学习这个有意义的课题——充分条件与必要条件。
【实例引入】
充分条件与必要条件:一般地,如果已知 那么就说,p 是q 的充分条件,q 是p 的必要条件.
两三角形全等是两三角形面积相等的充分条件.
两三角形面积相等是两三角形全等的必要条件.
两三角形全等 两三角形面积相等
例如:
定义:如果命题“若p,则q”为真命题,即p ? q, 那么我们就说p是q的充分条件;q是p的必要条件.
【定义得出】
①充分性:条件是充分的,也就是说条件是充足的,足够的,足以保证的。符合“若p则q”为真(p=>q)的形式,即“有之必成立”。
②必要性:必要就是必须的,必不可少的。符合“若非q则非p” 为真(非q=>非p)的形式,即“无之必不成立”。
注:
③p是q的充分条件与q是p的必要条件是完全等价的,它们是同一个逻辑关系“p=>q”的不同表达方法。
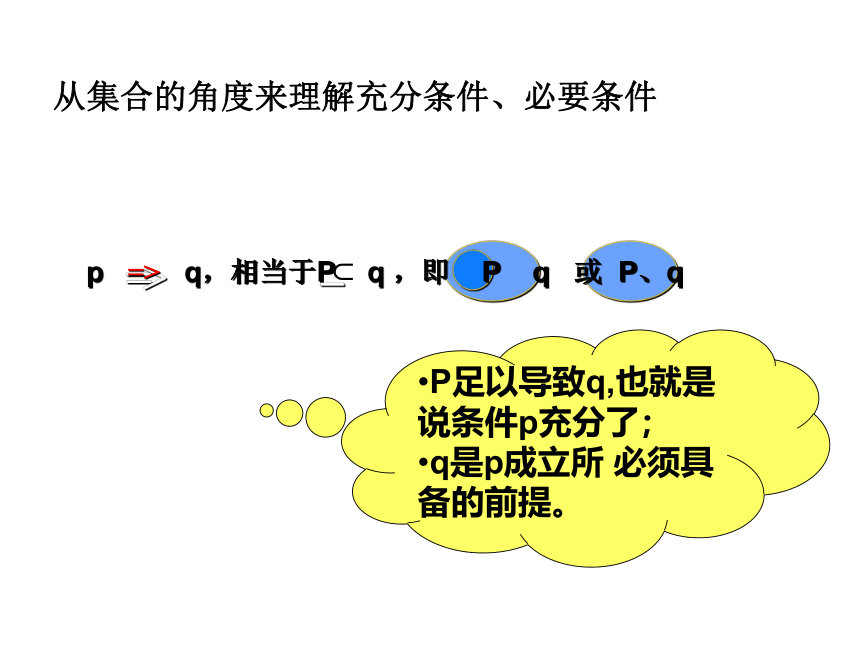
p => q,相当于P q ,即 P q 或 P、q
P足以导致q,也就是说条件p充分了;
q是p成立所 必须具备的前提。
从集合的角度来理解充分条件、必要条件
?
如果若p则q为假命题,那么由p推不出q,记作p q。此时,我们就说p不是q的充分条件,q不是p的必要条件。
能 力 测 试
1、用符号“充分”或“必要”填空:
(1)“0(2)“四边形的对角线相等”是“这个平行四边形
为正方形”的______条件。
(3)“xy > 0”是“ x+y = x + y ”的______条件。
(4)“个位数是5的整数”是“这个数能被5整除”
的________条件。
充分
必要
充分
充分
1、定义:
称:p是q的充分必要条件,简称充要条件
显然,如果p是q的充要条件,那么q也是p的充要条件
p与q互为充要条件
(也可以说成”p与q等价”)
1、充分且必要条件; 2、充分非必要条件;
3、必要非充分条件; 4、既不充分也不必要条件.
各种条件的可能情况:
充分不必要条件
必要不充分条件
既不充分也不必要条件
充分且必要条件
2、从逻辑推理关系看充分条件、必要条件:
1)A B且B A,则A是B的
2)若A B且B A,则A是B的
3)若A B且B A,则A是B的
4)A B且B A,则A是B的
3、从集合与集合的关系看充分条件、必要条件
① p q,相当于P Q ,即 P Q 或 P、Q
② q p,相当于Q P ,即 Q P 或 P、Q
有它就行
缺它不行
同一事物
③ p q,相当于P=Q ,即 P、Q
P、Q
口诀:对于具体的数集,以条件集合为基础,小充分,大必要.
充分非必要条件
必要非充分条件
既不充分也不必要条件
4)若A=B ,则甲是乙的
充分且必要条件
3、从集合与集合的关系看充分条件、必要条件
B
A
1 )
A
B
2 )
A
B
3 )
A = B
4 )
小结 充分必要条件的判断方法:
定义法、集合法、等价法(逆否命题)
2)若A B且B A,则甲是乙的
1)若A B且B A,则甲是乙的
3)若A B且B A,则甲是乙的
练习:请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空:
(1)“(x-2)(x-3)=0”是“x=2”的______条件.
(2)“同位角相等”是“两直线平行”的___条件.
(3)“x=3”是“x2=9”的______条件.
(4)“四边形的对角线相等”是“四边形为平行四边形”的__________条件.
充分不必要
必要不充分
充要
既不充分也不必要
P
O
Q
例4、 已知:⊙O的半径为r,圆心O到直线L的距离为d.
求证:d=r是直线L与⊙O相切的充要条件.
P
Q
O
证明:如图,作 于点P,则OP=d。
若d=r,则点P在 上。在直线 上任取一点Q(异于点P),连接OQ。
在 中,OQ>OP =r.
所以,除点P外直线 上的点都在 的外部,即直线 与 仅有一个公共点P。
所以直线 与 相切。
(1)充分性(p q):
若直线 与 相切,不妨设切点为P,则 .d=OP=r.
(2)必要性(q p):
所以,d=r是直线L与⊙O相切的充要条件.
1.设集合M={x|02.x>2的一个必要而不充分条件是_____________。
4. 的___________条件。
5.设p、r都是q的充分条件,s是q的充分必要条件,t是s的必要条件,t是r的充分条件,那么p是t的_______ 条件,r是t的________条件。
补充练习
必要而不充分
x>1
必要而不充分
充分不必要
充要
C
命题的4种情况:
1、命题:可以判断真假的陈述句
可以写成:若p则q。
故知新知
原命题 若 p则 q
逆命题 若 q则 p
否命题 若 p 则 q
逆否命题若 q 则 p
互逆
互逆
互否
互否
互为
逆否
同学们,当某一天你和你妈妈在街上遇到老师的时候,你向老师介绍你的妈妈说:“这是我的妈妈”。那么大家想一想这个时候你的妈妈还会不会补充说:“这是我的孩子”呢?
不会了!为什么呢?
因为前面你所介绍的她是你的妈妈就足以保证你是她的 孩子。那么,这在数学中是一层什么样的关系呢?今天我们就来学习这个有意义的课题——充分条件与必要条件。
【实例引入】
充分条件与必要条件:一般地,如果已知 那么就说,p 是q 的充分条件,q 是p 的必要条件.
两三角形全等是两三角形面积相等的充分条件.
两三角形面积相等是两三角形全等的必要条件.
两三角形全等 两三角形面积相等
例如:
定义:如果命题“若p,则q”为真命题,即p ? q, 那么我们就说p是q的充分条件;q是p的必要条件.
【定义得出】
①充分性:条件是充分的,也就是说条件是充足的,足够的,足以保证的。符合“若p则q”为真(p=>q)的形式,即“有之必成立”。
②必要性:必要就是必须的,必不可少的。符合“若非q则非p” 为真(非q=>非p)的形式,即“无之必不成立”。
注:
③p是q的充分条件与q是p的必要条件是完全等价的,它们是同一个逻辑关系“p=>q”的不同表达方法。
p => q,相当于P q ,即 P q 或 P、q
P足以导致q,也就是说条件p充分了;
q是p成立所 必须具备的前提。
从集合的角度来理解充分条件、必要条件
?
如果若p则q为假命题,那么由p推不出q,记作p q。此时,我们就说p不是q的充分条件,q不是p的必要条件。
能 力 测 试
1、用符号“充分”或“必要”填空:
(1)“0
为正方形”的______条件。
(3)“xy > 0”是“ x+y = x + y ”的______条件。
(4)“个位数是5的整数”是“这个数能被5整除”
的________条件。
充分
必要
充分
充分
1、定义:
称:p是q的充分必要条件,简称充要条件
显然,如果p是q的充要条件,那么q也是p的充要条件
p与q互为充要条件
(也可以说成”p与q等价”)
1、充分且必要条件; 2、充分非必要条件;
3、必要非充分条件; 4、既不充分也不必要条件.
各种条件的可能情况:
充分不必要条件
必要不充分条件
既不充分也不必要条件
充分且必要条件
2、从逻辑推理关系看充分条件、必要条件:
1)A B且B A,则A是B的
2)若A B且B A,则A是B的
3)若A B且B A,则A是B的
4)A B且B A,则A是B的
3、从集合与集合的关系看充分条件、必要条件
① p q,相当于P Q ,即 P Q 或 P、Q
② q p,相当于Q P ,即 Q P 或 P、Q
有它就行
缺它不行
同一事物
③ p q,相当于P=Q ,即 P、Q
P、Q
口诀:对于具体的数集,以条件集合为基础,小充分,大必要.
充分非必要条件
必要非充分条件
既不充分也不必要条件
4)若A=B ,则甲是乙的
充分且必要条件
3、从集合与集合的关系看充分条件、必要条件
B
A
1 )
A
B
2 )
A
B
3 )
A = B
4 )
小结 充分必要条件的判断方法:
定义法、集合法、等价法(逆否命题)
2)若A B且B A,则甲是乙的
1)若A B且B A,则甲是乙的
3)若A B且B A,则甲是乙的
练习:请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空:
(1)“(x-2)(x-3)=0”是“x=2”的______条件.
(2)“同位角相等”是“两直线平行”的___条件.
(3)“x=3”是“x2=9”的______条件.
(4)“四边形的对角线相等”是“四边形为平行四边形”的__________条件.
充分不必要
必要不充分
充要
既不充分也不必要
P
O
Q
例4、 已知:⊙O的半径为r,圆心O到直线L的距离为d.
求证:d=r是直线L与⊙O相切的充要条件.
P
Q
O
证明:如图,作 于点P,则OP=d。
若d=r,则点P在 上。在直线 上任取一点Q(异于点P),连接OQ。
在 中,OQ>OP =r.
所以,除点P外直线 上的点都在 的外部,即直线 与 仅有一个公共点P。
所以直线 与 相切。
(1)充分性(p q):
若直线 与 相切,不妨设切点为P,则 .d=OP=r.
(2)必要性(q p):
所以,d=r是直线L与⊙O相切的充要条件.
1.设集合M={x|0
4. 的___________条件。
5.设p、r都是q的充分条件,s是q的充分必要条件,t是s的必要条件,t是r的充分条件,那么p是t的_______ 条件,r是t的________条件。
补充练习
必要而不充分
x>1
必要而不充分
充分不必要
充要
C
命题的4种情况:
同课章节目录
