1.5.3定积分的概念-人教版高中数学选修2-2课件(19张PPT)
文档属性
| 名称 | 1.5.3定积分的概念-人教版高中数学选修2-2课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 09:48:46 | ||
图片预览



文档简介
1.5.3 定积分的概念
割圆术???
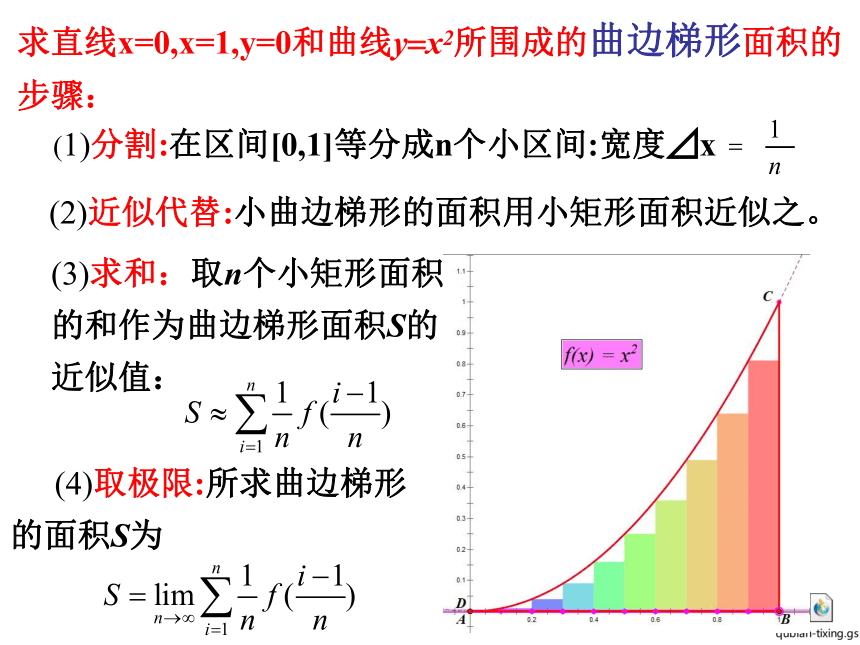
求直线x=0,x=1,y=0和曲线y=x2所围成的曲边梯形面积的步骤:
(2)近似代替:小曲边梯形的面积用小矩形面积近似之。
(4)取极限:所求曲边梯形的面积S为
(3)求和:取n个小矩形面积的和作为曲边梯形面积S的近似值:
(1)分割:在区间[0,1]等分成n个小区间:宽度⊿x
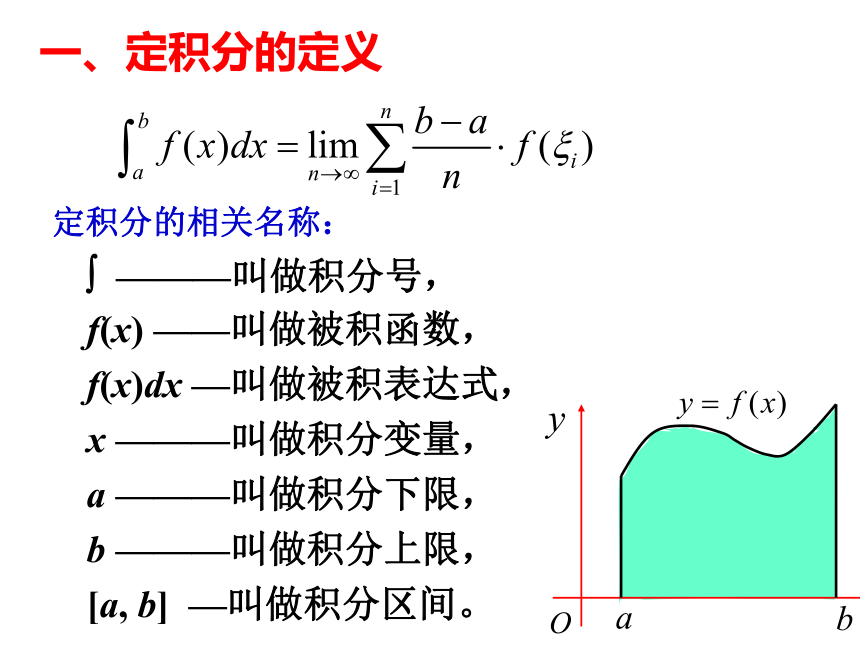
一、定积分的定义
定积分的相关名称:
? ———叫做积分号,
f(x) ——叫做被积函数,
f(x)dx —叫做被积表达式,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。
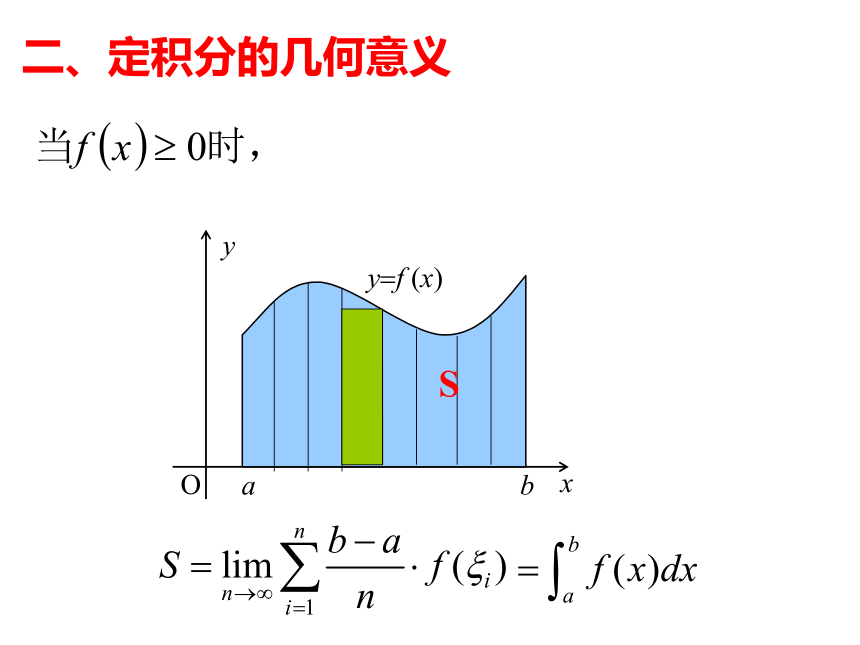
二、定积分的几何意义
O
x
y
a
b
y?f (x)
S
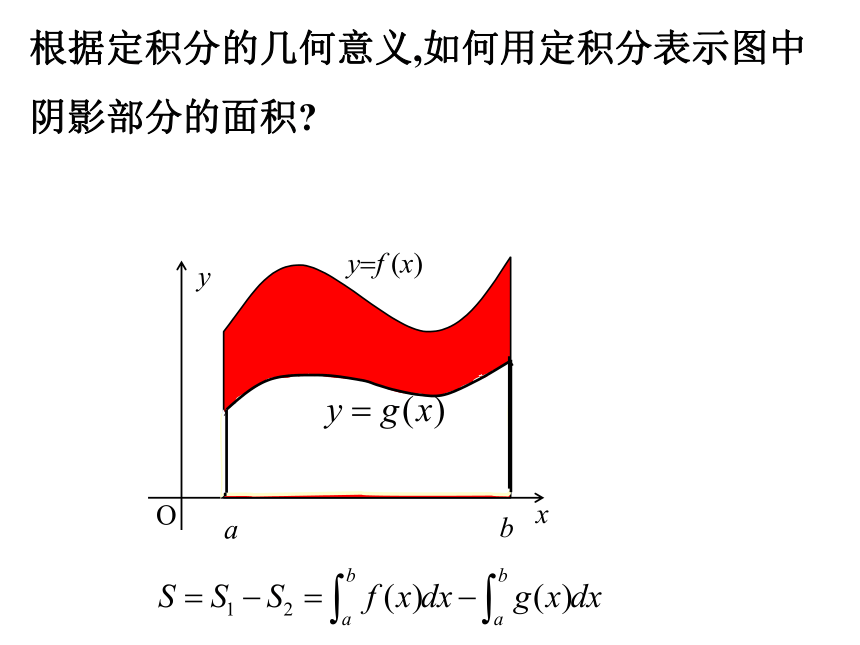
根据定积分的几何意义,如何用定积分表示图中阴影部分的面积?
a
b
y?f (x)
O
x
y
x
y
O
a
b
y?f (x)
y?-f (x)
=-S
探究1:
思考2:
根据定积分的几何意义,如何用定积分表示图中阴影部分的面积?
O
x
y
y?f (x)
b
a
y?g(x)
结论:
三: 定积分的基本性质
性质1.
性质2.
三: 定积分的基本性质
定积分关于积分区间具有可加性
性质3.
O
x
y
a
b
y?f (x)
c
例1:利用几何意义计算
变式1:
4
2
4
0
-1
-6
x
y
解:
x
y
f(x)=sinx
1
-1
例2:利用几何意义计算
(1)若奇函数 的图像在
上连续,则
(2)若偶函数 的图像在
上连续,则
结论:
x
1
y
变式2:
探究2:
思考:
(1)你觉得这个定积分可以表示成什么的图形?
(2)依据是什么?
(3)你能画出这个图形吗?
1、定积分的概念
2、几何意义
小结
1、书本P50,A组T1~T5;
2、搜集历史上我国和古代欧洲有关微积分思想的一些代表性的工作。
作业
小组评分
组别
得分
第一组
第二组
第三组
第四组
第五组
第六组
谢谢!
割圆术???
求直线x=0,x=1,y=0和曲线y=x2所围成的曲边梯形面积的步骤:
(2)近似代替:小曲边梯形的面积用小矩形面积近似之。
(4)取极限:所求曲边梯形的面积S为
(3)求和:取n个小矩形面积的和作为曲边梯形面积S的近似值:
(1)分割:在区间[0,1]等分成n个小区间:宽度⊿x
一、定积分的定义
定积分的相关名称:
? ———叫做积分号,
f(x) ——叫做被积函数,
f(x)dx —叫做被积表达式,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。
二、定积分的几何意义
O
x
y
a
b
y?f (x)
S
根据定积分的几何意义,如何用定积分表示图中阴影部分的面积?
a
b
y?f (x)
O
x
y
x
y
O
a
b
y?f (x)
y?-f (x)
=-S
探究1:
思考2:
根据定积分的几何意义,如何用定积分表示图中阴影部分的面积?
O
x
y
y?f (x)
b
a
y?g(x)
结论:
三: 定积分的基本性质
性质1.
性质2.
三: 定积分的基本性质
定积分关于积分区间具有可加性
性质3.
O
x
y
a
b
y?f (x)
c
例1:利用几何意义计算
变式1:
4
2
4
0
-1
-6
x
y
解:
x
y
f(x)=sinx
1
-1
例2:利用几何意义计算
(1)若奇函数 的图像在
上连续,则
(2)若偶函数 的图像在
上连续,则
结论:
x
1
y
变式2:
探究2:
思考:
(1)你觉得这个定积分可以表示成什么的图形?
(2)依据是什么?
(3)你能画出这个图形吗?
1、定积分的概念
2、几何意义
小结
1、书本P50,A组T1~T5;
2、搜集历史上我国和古代欧洲有关微积分思想的一些代表性的工作。
作业
小组评分
组别
得分
第一组
第二组
第三组
第四组
第五组
第六组
谢谢!
