2.2.1 空间向量及其加减运算-北师大版高中数学选修2-1课件(16张PPT)
文档属性
| 名称 | 2.2.1 空间向量及其加减运算-北师大版高中数学选修2-1课件(16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 09:50:57 | ||
图片预览


文档简介
空间向量
及其加减运算
用字母 等或者用有向线段
的起点与终点字母 表示.
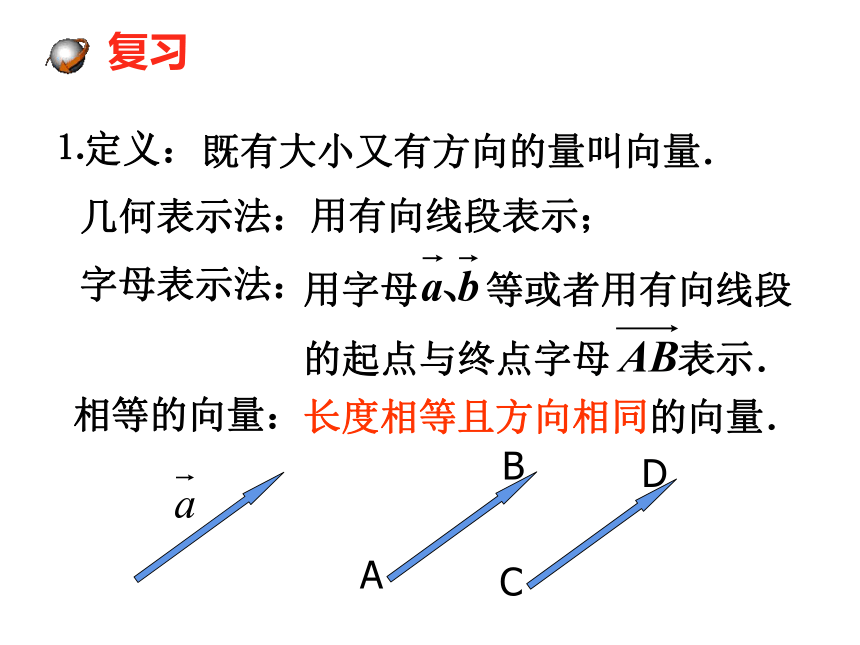
⒈定义:
既有大小又有方向的量叫向量.
几何表示法:
用有向线段表示;
字母表示法:
相等的向量:
长度相等且方向相同的向量.
A
B
C
D
复习
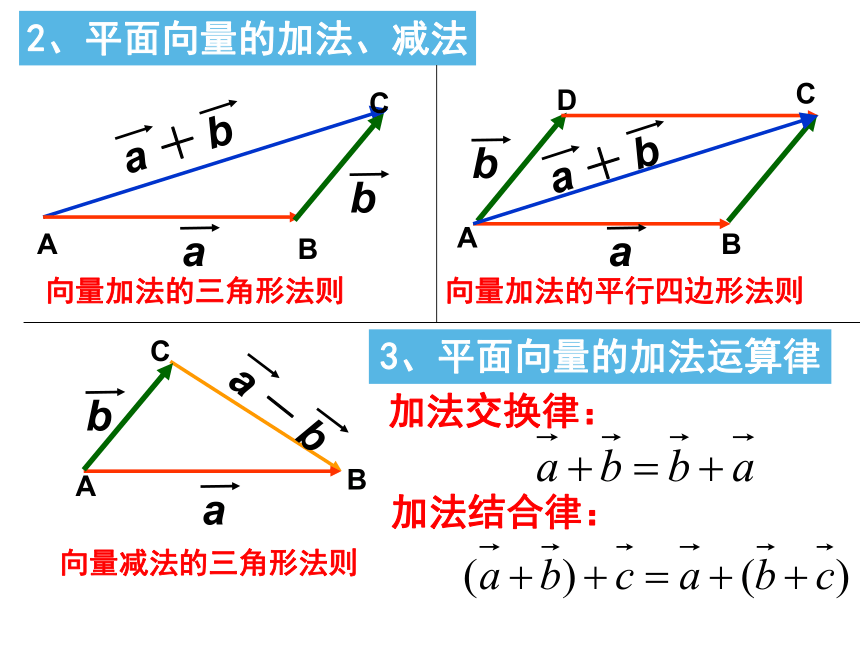
2、平面向量的加法、减法
向量加法的三角形法则
向量加法的平行四边形法则
向量减法的三角形法则
a -
b
a +
b
a
A
B
b
C
a
A
B
b
D
C
a
A
B
b
C
a +
b
3、平面向量的加法运算律
加法交换律:
加法结合律:
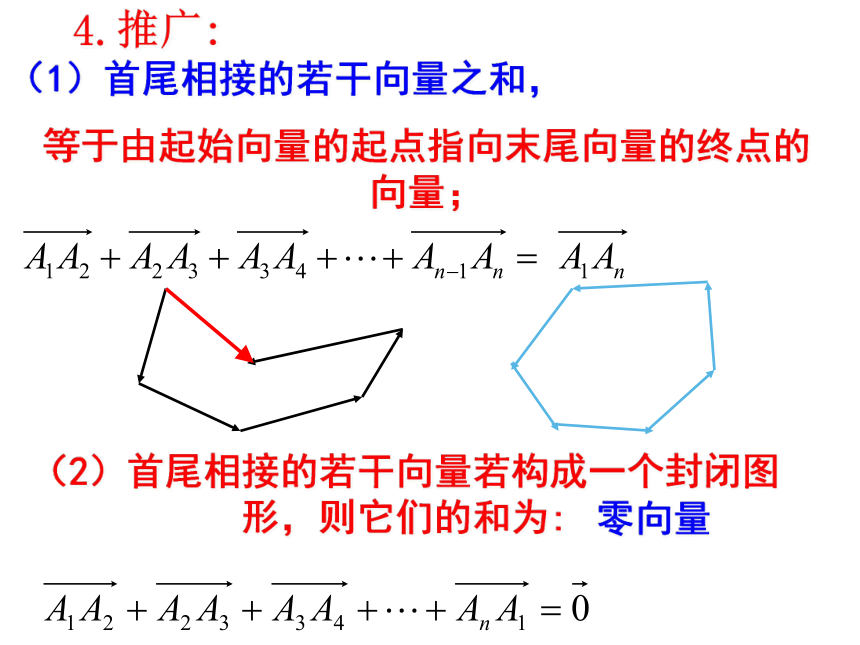
4.推广:
(1)首尾相接的若干向量之和,
(2)首尾相接的若干向量若构成一个封闭图
形,则它们的和为:
等于由起始向量的起点指向末尾向量的终点的向量;
零向量
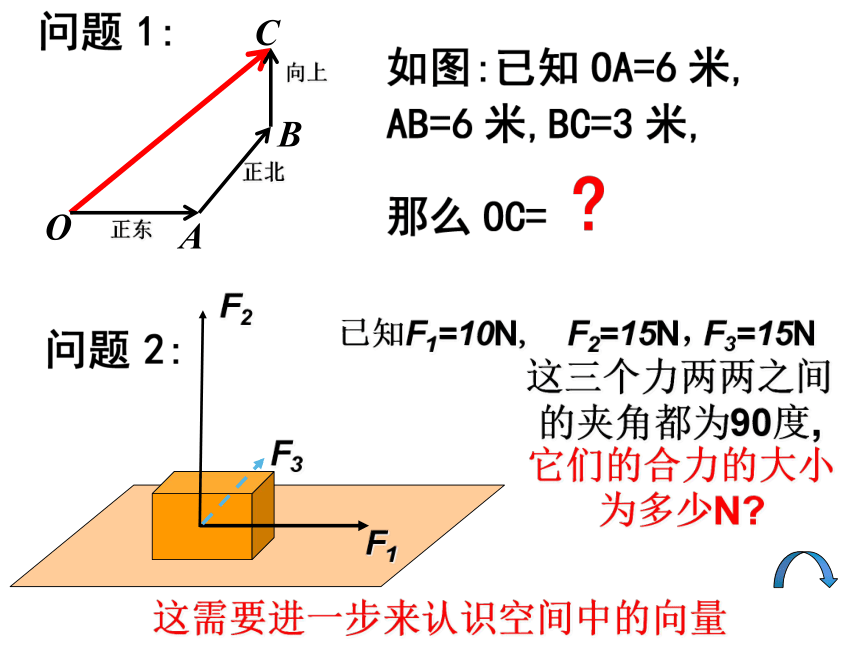
正东
正北
向上
F3=15N
已知F1=10N,
F2=15N,
F3
F1
F2
这三个力两两之间的夹角都为90度,
它们的合力的大小为多少N?
这需要进一步来认识空间中的向量
a
b
a
b
a
b
+
O
A
B
b
C
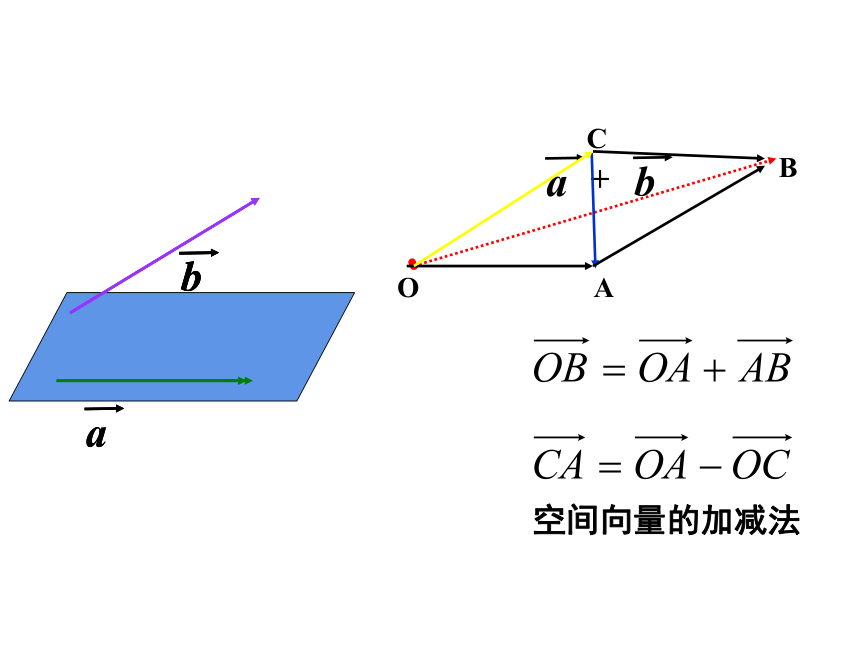
空间向量的加减法
a
b
O
A
B
b
a
结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们.
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量的加法、减法运算
空间向量
具有大小和方向的量
加法交换律
加法结合律
加法交换律
加法:三角形法则或
平行四边形法则
减法:三角形法则
加法结合律
成立吗?
(1)加法交换律:
(2)加法结合律:
a
b
c
a + b + c
a
b
c
a + b + c
a + b
b + c
空间向量的加法、减法运算
(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
推广
(2)首尾相接的若干向量构成一个封闭图形,
则它们的和为零向量.即:
推广
解:
A
B
C
D
A’
B’
C’
D’
例题
解:
A
B
C
D
A’
B’
C’
D’
例题
起点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共起点为起点的对角线所示向量
A
B
C
D
A’
B’
C’
D’
例题
正东
正北
向上
F3=15N
已知F1=10N,
F2=15N,
F3
F1
F2
这三个力两两之间的夹角都为90度,
它们的合力的大小为多少N?
你能解决吗?
加法交换律
加法:三角形法则或
平行四边形法则
减法:三角形法则
加法结合律
在这里,空间向量的加减法运算性质
完全和平面向量的运算性质一样!
及其加减运算
用字母 等或者用有向线段
的起点与终点字母 表示.
⒈定义:
既有大小又有方向的量叫向量.
几何表示法:
用有向线段表示;
字母表示法:
相等的向量:
长度相等且方向相同的向量.
A
B
C
D
复习
2、平面向量的加法、减法
向量加法的三角形法则
向量加法的平行四边形法则
向量减法的三角形法则
a -
b
a +
b
a
A
B
b
C
a
A
B
b
D
C
a
A
B
b
C
a +
b
3、平面向量的加法运算律
加法交换律:
加法结合律:
4.推广:
(1)首尾相接的若干向量之和,
(2)首尾相接的若干向量若构成一个封闭图
形,则它们的和为:
等于由起始向量的起点指向末尾向量的终点的向量;
零向量
正东
正北
向上
F3=15N
已知F1=10N,
F2=15N,
F3
F1
F2
这三个力两两之间的夹角都为90度,
它们的合力的大小为多少N?
这需要进一步来认识空间中的向量
a
b
a
b
a
b
+
O
A
B
b
C
空间向量的加减法
a
b
O
A
B
b
a
结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们.
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量的加法、减法运算
空间向量
具有大小和方向的量
加法交换律
加法结合律
加法交换律
加法:三角形法则或
平行四边形法则
减法:三角形法则
加法结合律
成立吗?
(1)加法交换律:
(2)加法结合律:
a
b
c
a + b + c
a
b
c
a + b + c
a + b
b + c
空间向量的加法、减法运算
(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
推广
(2)首尾相接的若干向量构成一个封闭图形,
则它们的和为零向量.即:
推广
解:
A
B
C
D
A’
B’
C’
D’
例题
解:
A
B
C
D
A’
B’
C’
D’
例题
起点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共起点为起点的对角线所示向量
A
B
C
D
A’
B’
C’
D’
例题
正东
正北
向上
F3=15N
已知F1=10N,
F2=15N,
F3
F1
F2
这三个力两两之间的夹角都为90度,
它们的合力的大小为多少N?
你能解决吗?
加法交换律
加法:三角形法则或
平行四边形法则
减法:三角形法则
加法结合律
在这里,空间向量的加减法运算性质
完全和平面向量的运算性质一样!
同课章节目录
