2.2.2空间向量数乘运算-北师大版高中数学选修2-1课件(15张PPT)
文档属性
| 名称 | 2.2.2空间向量数乘运算-北师大版高中数学选修2-1课件(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 807.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 09:52:21 | ||
图片预览




文档简介
———共线向量与共面向量
一、空间向量数乘运算
1.实数 与空间向量 的乘积 仍然是一个向量.
当 时,
当 时,
与向量 方向相同;
与向量 方向相同;
是零向量.
当 时,
(1)方向:
(2)大小:
的长度是 的长度的 倍.
2.空间向量的数乘运算满足分配律及结合律
问题2:平面向量中,
的充要条件是:存在唯一
的实数 ,使
能否推广到空间向量中呢?
问题1:若
则
所在直线有那些位置关系?
零向量与任意向量共线.
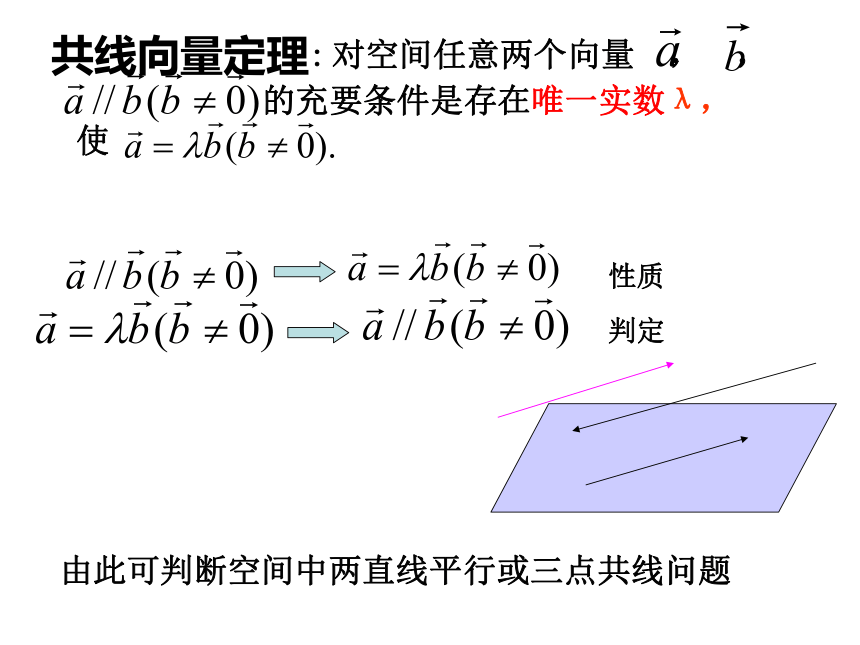
二、共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作
由此可判断空间中两直线平行或三点共线问题
共线向量定理: 对空间任意两个向量 , ,
的充要条件是存在唯一实数λ,
使
性质
判定
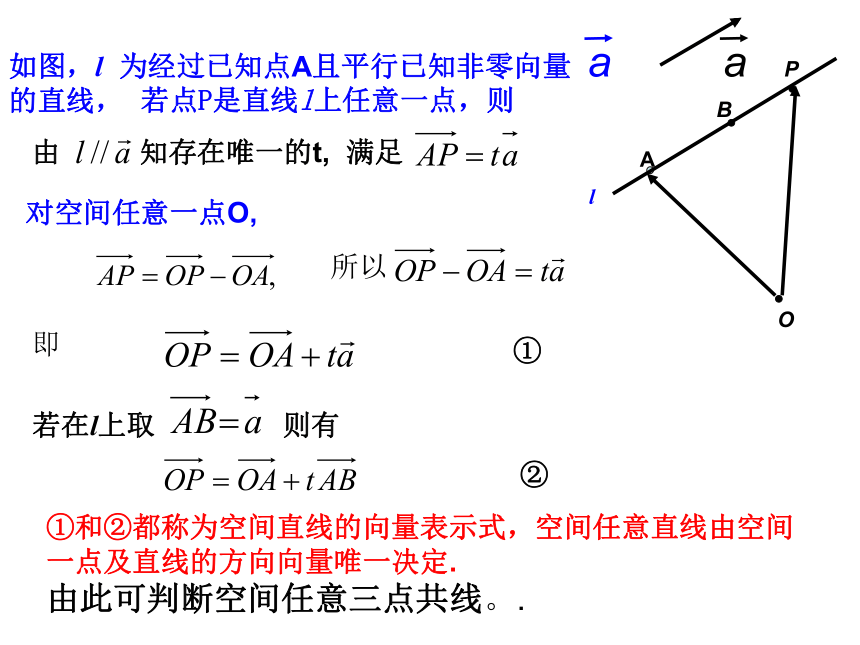
如图,l 为经过已知点A且平行已知非零向量 的直线,
a
对空间任意一点O,
所以
即
若在l上取 则有
①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量唯一决定.
由此可判断空间任意三点共线。.
a
l
A
B
P
O
若点P是直线l上任意一点,则
由 知存在唯一的t, 满足
①
②
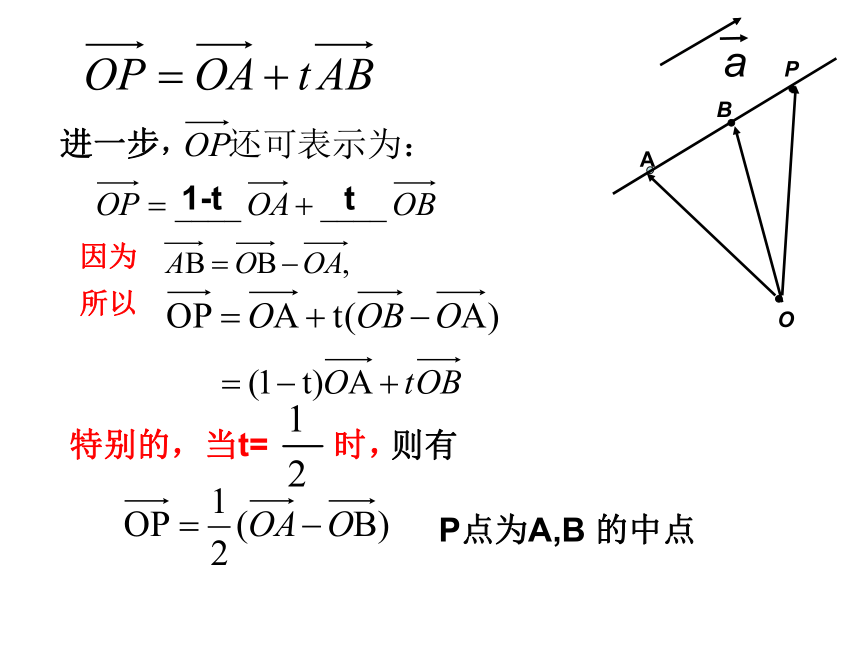
因为
所以
特别的,当t= 时,
则有
a
A
B
P
O
进一步,
t
1-t
P点为A,B 的中点
练习1.对于空间任意一点O,下列命题正确的是:
A.若 ,则P、A、B共线
B.若 ,则P是AB的中点
C.若 ,则P、A、B不共线
D.若 ,则P、A、B共线
A、B、P三点共线
A
O
A
B
P
三、共面向量:
1.共面向量:平行于同一平面的向量,叫做共面向量.
注意:空间任意两个向量是共面的,但空间任意三个向量
既可能共面,也可能不共面
d
b
a
c
由平面向量基本定理知,如果 ,
是平面内的两个不共线的向量,那么
对于这一平面内的任意向量 ,有且只有一对实数 , 使
如果空间向量 与两不共线向量 , 共
面,那么可将三个向量平移到同一平面 ,则
有
那么什么情况下三个向量共面呢?
反过来,对空间任意两个不共线的向量 , ,如果 ,那么向量 与向量 , 有什么位
置关系?
C
2.共面向量定理:如果两个向量 , 不共线,
则向量 与向量 , 共面的充要条件是
存在实数对x,y使
推论:空间一点P位于平面ABC内的充要条件是存在有
序实数对x,y使
C
对空间任一点O,有
填空:
1-x-y
x
y
C
③
由此可判断空间任意四点共面
练习2.若对任一点O和不共线的三点A、B、C,
且有
则x+y+z=1
是四点P、A、B、C共面的( )
A.必要不充分条件
C.充要条件
B.充分不必要条件
D.既不充分也不必要条件
C
P与A,B,C共面
共线向量
共面向量
定义
向量所在直线互相平行或重合
平行于同一平面的向量,叫做共面向量.
定理
推论
运用
判断三点共线,或两直线平行
判断四点共线,或直线平行于平面
小结
共面
一、空间向量数乘运算
1.实数 与空间向量 的乘积 仍然是一个向量.
当 时,
当 时,
与向量 方向相同;
与向量 方向相同;
是零向量.
当 时,
(1)方向:
(2)大小:
的长度是 的长度的 倍.
2.空间向量的数乘运算满足分配律及结合律
问题2:平面向量中,
的充要条件是:存在唯一
的实数 ,使
能否推广到空间向量中呢?
问题1:若
则
所在直线有那些位置关系?
零向量与任意向量共线.
二、共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作
由此可判断空间中两直线平行或三点共线问题
共线向量定理: 对空间任意两个向量 , ,
的充要条件是存在唯一实数λ,
使
性质
判定
如图,l 为经过已知点A且平行已知非零向量 的直线,
a
对空间任意一点O,
所以
即
若在l上取 则有
①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量唯一决定.
由此可判断空间任意三点共线。.
a
l
A
B
P
O
若点P是直线l上任意一点,则
由 知存在唯一的t, 满足
①
②
因为
所以
特别的,当t= 时,
则有
a
A
B
P
O
进一步,
t
1-t
P点为A,B 的中点
练习1.对于空间任意一点O,下列命题正确的是:
A.若 ,则P、A、B共线
B.若 ,则P是AB的中点
C.若 ,则P、A、B不共线
D.若 ,则P、A、B共线
A、B、P三点共线
A
O
A
B
P
三、共面向量:
1.共面向量:平行于同一平面的向量,叫做共面向量.
注意:空间任意两个向量是共面的,但空间任意三个向量
既可能共面,也可能不共面
d
b
a
c
由平面向量基本定理知,如果 ,
是平面内的两个不共线的向量,那么
对于这一平面内的任意向量 ,有且只有一对实数 , 使
如果空间向量 与两不共线向量 , 共
面,那么可将三个向量平移到同一平面 ,则
有
那么什么情况下三个向量共面呢?
反过来,对空间任意两个不共线的向量 , ,如果 ,那么向量 与向量 , 有什么位
置关系?
C
2.共面向量定理:如果两个向量 , 不共线,
则向量 与向量 , 共面的充要条件是
存在实数对x,y使
推论:空间一点P位于平面ABC内的充要条件是存在有
序实数对x,y使
C
对空间任一点O,有
填空:
1-x-y
x
y
C
③
由此可判断空间任意四点共面
练习2.若对任一点O和不共线的三点A、B、C,
且有
则x+y+z=1
是四点P、A、B、C共面的( )
A.必要不充分条件
C.充要条件
B.充分不必要条件
D.既不充分也不必要条件
C
P与A,B,C共面
共线向量
共面向量
定义
向量所在直线互相平行或重合
平行于同一平面的向量,叫做共面向量.
定理
推论
运用
判断三点共线,或两直线平行
判断四点共线,或直线平行于平面
小结
共面
同课章节目录
