2.2.3空间向量的数量积运算-北师大版高中数学选修2-1课件(18张PPT)
文档属性
| 名称 | 2.2.3空间向量的数量积运算-北师大版高中数学选修2-1课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 09:53:12 | ||
图片预览






文档简介
空间向量的
数量积运算
A
O
B
a
b
a
b
a
b
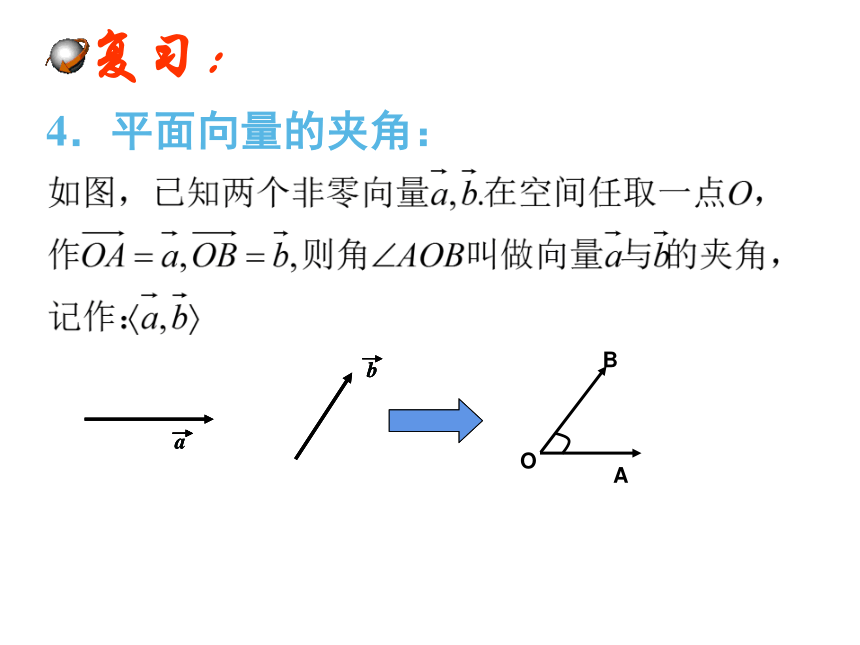
4.平面向量的夹角:
复习:
1) 空间两个向量的夹角的定义
思考:1、〈a,b〉与〈b,a〉相等吗?
2、〈a,b〉与〈a,-b〉相等吗?
注意:〈a,b〉=〈b,a〉,〈a,-b〉=π-〈a,b〉
两条相交直线的夹角是指这两条直线所成的锐角或直角,即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]
A
B
A'
B'
3、射影
l
2)两个向量的数量积
注:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
3)空间向量的数量积性质:
对于非零向量 ,有:
(求角的依据)
(证明垂直的依据)
(求向量的长度的依据)
4)空间向量的数量积满足的运算律
下列命题成立吗?
①若 ,则
②若 ,则
③
思考:
3、空间向量数量积的性质
4. 空间向量数量积运算律
⑴
⑵
⑶
(数乘结合律)
(分配律)
(交换律)
注意:
数量积不满足结合律,
也不满足消去率
1.向量a、b之间的夹角为30°,且|a|=3,
| b |=4,则a·b =__________, a2=__________,
(a+2b)·(a-b)=__________.
题型一 利用数量积求夹角
如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC所成角的余弦值.
【例1】
如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC所成角的余弦值.
分析:用向量来证明两直线垂直,只需证明两直线的方向向量的数量积为零即可!
题型二 利用数量积证明垂直关系
【例2】
证明:
如图,已知:
求证:
在直线l上取向量 ,只要证
为
分析:同样可用向量,证明思路几乎一样,只不过其中的加法运算用减法运算来分析.
解:
2.已知在平行六面体
,
求 对角线的长.
巩固练习:
空间向量数量积的定义
空间向量数量积的性质
空间向量数量积的运用
空间向量的夹角
数量积运算
A
O
B
a
b
a
b
a
b
4.平面向量的夹角:
复习:
1) 空间两个向量的夹角的定义
思考:1、〈a,b〉与〈b,a〉相等吗?
2、〈a,b〉与〈a,-b〉相等吗?
注意:〈a,b〉=〈b,a〉,〈a,-b〉=π-〈a,b〉
两条相交直线的夹角是指这两条直线所成的锐角或直角,即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]
A
B
A'
B'
3、射影
l
2)两个向量的数量积
注:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
3)空间向量的数量积性质:
对于非零向量 ,有:
(求角的依据)
(证明垂直的依据)
(求向量的长度的依据)
4)空间向量的数量积满足的运算律
下列命题成立吗?
①若 ,则
②若 ,则
③
思考:
3、空间向量数量积的性质
4. 空间向量数量积运算律
⑴
⑵
⑶
(数乘结合律)
(分配律)
(交换律)
注意:
数量积不满足结合律,
也不满足消去率
1.向量a、b之间的夹角为30°,且|a|=3,
| b |=4,则a·b =__________, a2=__________,
(a+2b)·(a-b)=__________.
题型一 利用数量积求夹角
如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC所成角的余弦值.
【例1】
如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC所成角的余弦值.
分析:用向量来证明两直线垂直,只需证明两直线的方向向量的数量积为零即可!
题型二 利用数量积证明垂直关系
【例2】
证明:
如图,已知:
求证:
在直线l上取向量 ,只要证
为
分析:同样可用向量,证明思路几乎一样,只不过其中的加法运算用减法运算来分析.
解:
2.已知在平行六面体
,
求 对角线的长.
巩固练习:
空间向量数量积的定义
空间向量数量积的性质
空间向量数量积的运用
空间向量的夹角
同课章节目录
