2.3向量的坐标表示和空间向量的基本定理-北师大版高中数学选修2-1课件(32张PPT)
文档属性
| 名称 | 2.3向量的坐标表示和空间向量的基本定理-北师大版高中数学选修2-1课件(32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 09:54:05 | ||
图片预览









文档简介
3.1.4空间向量的正交 分解及其坐标表示
平面向量基本定理:
平面向量的正交分解及坐标表示
x
y
o
复习:
在空间中,能得出类似的结论:
任意不共面的三个向量都可做为空间的一个基底。
一、空间向量基本定理:
如果三个向量 不共面,那么对空间任一向量 ,存在一个唯一的有序实数组x,y,z,使
都叫做基向量
(1)任意不共面的三个向量都可做为空间的一个基底。
注:对于基底{a,b,c},除了应知道a,b,c不共面,
还应明确:
(2) 由于可视 为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 。
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关连的不同概念。
x
y
z
O
Q
P
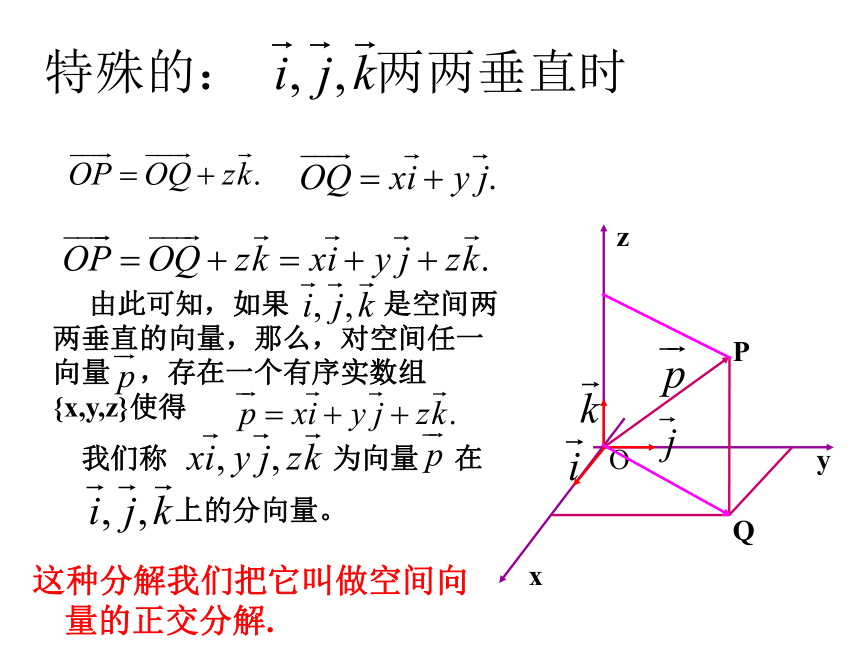
由此可知,如果 是空间两两垂直的向量,那么,对空间任一向量 ,存在一个有序实数组 {x,y,z}使得
我们称 为向量 在
上的分向量。
这种分解我们把它叫做空间向量的正交分解.
二、空间直角坐标系下空间向量的直角坐标
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,常用e1 , e2 , e3 表示
x
y
z
O
A(x,y,z)
e1
e2
e3
空间向量的直角坐标:
给定一个空间坐标系和向量 ,且设e1,e2,e3为坐标向量,由空间向量基本定理,存在唯一的有序实数组(x,y, z)使
p = xe1+ye2+ze3
有序数组( x, y, z)叫做p在空间直角坐标系O--xyz中的坐标,记作.P=(x,y,z)其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标.
C1
D
A1
O
B
C
z
x
y
(A)
D1
B1
解: (1)因为AB=2,BC=3,AA1=5
所以C1为(3,2,5)
(2)因为点D1为(3,0,5)
A
D1
C1
B1
A1
D
C
B
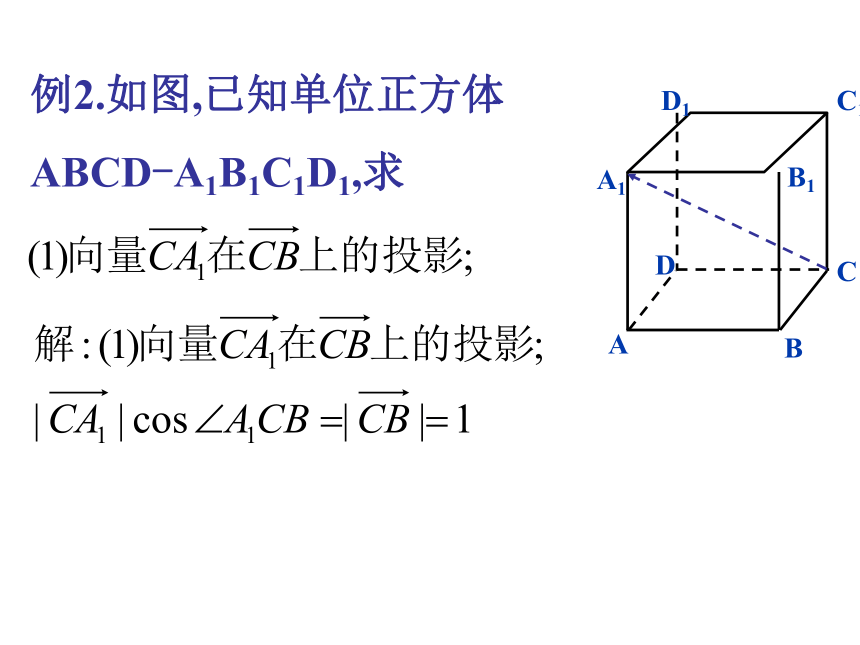
例2.如图,已知单位正方体
ABCD-A1B1C1D1,求
A
D1
C1
B1
A1
D
C
B
例2.如图,已知单位正方体
ABCD-A1B1C1D1,求
(1)不共线的向量 叫做这一平面内所有向量 的一组基底;
平面向量基本定理:
(4)基底给定时,分解形式唯一.
如果 是同一平面内的两个不共线向量,那么对这一平面内的任一向量 ,有且只有一对实数 ,
使
(3) 任一向量 都可以沿两个不共线的方向( 的
方向)分解成两个向量( )和的形式;
说明:
例题讲解
空间向量运算
的坐标表示
O
x
y
z
从空间某一个定点O引三条互相垂直且有相同单位长度的数轴,这样就建立了空间直角坐标系O-xyz.
点O叫作坐标原点,x,y,z轴统称为坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xOy平面、 yOz平面和 xOz平面.
空间直角坐标系
右手系:伸出右手,让四指与大拇指垂直,并使四
指先指向x轴正方向,然后让四指沿握拳方向旋转
指向y轴正方向,此时大拇指的指向即为z轴正向.我们也称这样的坐标系为右手系.
说明:
☆本书建立的坐标系
都是右手直角坐标系.
Ⅶ
面
面
面
空间直角坐标系共有八个卦限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
Ⅵ
Ⅷ
, 则
设
一、向量的直角坐标运算
若A(x1,y1,z1),B(x2,y2,z2), 则
AB
=
OB-OA=(x2,y2,z2)-(x1,y1,z1)
=(x2-x1 , y2-y1 , z2-z1)
空间一个向量在直角坐标系中的坐标等于表示这个
向量的有向线段的终点的坐标减去起点的坐标.
二、距离与夹角的坐标表示
1.距离公式
(1)向量的长度(模)公式
注意:此公式的几何意义是表示长方体的对角线的长度。
在空间直角坐标系中,已知 、
,则
(2)空间两点间的距离公式
2.两个向量夹角公式
注意:
(1)当 时, 同向;
(2)当 时, 反向;
(3)当 时, 。
4空间向量平行和垂直的条件
例1.已知
解:
三、应用举例
三、应用举例
例2 已知 、 ,求:
(1)线段 的中点坐标和长度;
解:设 是 的中点,则
∴点 的坐标是 .
解:设正方体的棱长为1,如图建
立空间直角坐标系 ,则
例3 如图, 在正方体 中,
,求 与 所成的角的余弦值.
证明:
设正方体的棱长为1,
建立如图的空间直角坐标系
x
y
z
A1
D1
C1
B1
A
C
B
D
F
E
平面向量基本定理:
平面向量的正交分解及坐标表示
x
y
o
复习:
在空间中,能得出类似的结论:
任意不共面的三个向量都可做为空间的一个基底。
一、空间向量基本定理:
如果三个向量 不共面,那么对空间任一向量 ,存在一个唯一的有序实数组x,y,z,使
都叫做基向量
(1)任意不共面的三个向量都可做为空间的一个基底。
注:对于基底{a,b,c},除了应知道a,b,c不共面,
还应明确:
(2) 由于可视 为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 。
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关连的不同概念。
x
y
z
O
Q
P
由此可知,如果 是空间两两垂直的向量,那么,对空间任一向量 ,存在一个有序实数组 {x,y,z}使得
我们称 为向量 在
上的分向量。
这种分解我们把它叫做空间向量的正交分解.
二、空间直角坐标系下空间向量的直角坐标
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,常用e1 , e2 , e3 表示
x
y
z
O
A(x,y,z)
e1
e2
e3
空间向量的直角坐标:
给定一个空间坐标系和向量 ,且设e1,e2,e3为坐标向量,由空间向量基本定理,存在唯一的有序实数组(x,y, z)使
p = xe1+ye2+ze3
有序数组( x, y, z)叫做p在空间直角坐标系O--xyz中的坐标,记作.P=(x,y,z)其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标.
C1
D
A1
O
B
C
z
x
y
(A)
D1
B1
解: (1)因为AB=2,BC=3,AA1=5
所以C1为(3,2,5)
(2)因为点D1为(3,0,5)
A
D1
C1
B1
A1
D
C
B
例2.如图,已知单位正方体
ABCD-A1B1C1D1,求
A
D1
C1
B1
A1
D
C
B
例2.如图,已知单位正方体
ABCD-A1B1C1D1,求
(1)不共线的向量 叫做这一平面内所有向量 的一组基底;
平面向量基本定理:
(4)基底给定时,分解形式唯一.
如果 是同一平面内的两个不共线向量,那么对这一平面内的任一向量 ,有且只有一对实数 ,
使
(3) 任一向量 都可以沿两个不共线的方向( 的
方向)分解成两个向量( )和的形式;
说明:
例题讲解
空间向量运算
的坐标表示
O
x
y
z
从空间某一个定点O引三条互相垂直且有相同单位长度的数轴,这样就建立了空间直角坐标系O-xyz.
点O叫作坐标原点,x,y,z轴统称为坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xOy平面、 yOz平面和 xOz平面.
空间直角坐标系
右手系:伸出右手,让四指与大拇指垂直,并使四
指先指向x轴正方向,然后让四指沿握拳方向旋转
指向y轴正方向,此时大拇指的指向即为z轴正向.我们也称这样的坐标系为右手系.
说明:
☆本书建立的坐标系
都是右手直角坐标系.
Ⅶ
面
面
面
空间直角坐标系共有八个卦限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
Ⅵ
Ⅷ
, 则
设
一、向量的直角坐标运算
若A(x1,y1,z1),B(x2,y2,z2), 则
AB
=
OB-OA=(x2,y2,z2)-(x1,y1,z1)
=(x2-x1 , y2-y1 , z2-z1)
空间一个向量在直角坐标系中的坐标等于表示这个
向量的有向线段的终点的坐标减去起点的坐标.
二、距离与夹角的坐标表示
1.距离公式
(1)向量的长度(模)公式
注意:此公式的几何意义是表示长方体的对角线的长度。
在空间直角坐标系中,已知 、
,则
(2)空间两点间的距离公式
2.两个向量夹角公式
注意:
(1)当 时, 同向;
(2)当 时, 反向;
(3)当 时, 。
4空间向量平行和垂直的条件
例1.已知
解:
三、应用举例
三、应用举例
例2 已知 、 ,求:
(1)线段 的中点坐标和长度;
解:设 是 的中点,则
∴点 的坐标是 .
解:设正方体的棱长为1,如图建
立空间直角坐标系 ,则
例3 如图, 在正方体 中,
,求 与 所成的角的余弦值.
证明:
设正方体的棱长为1,
建立如图的空间直角坐标系
x
y
z
A1
D1
C1
B1
A
C
B
D
F
E
同课章节目录
