2.5夹角的计算-北师大版高中数学选修2-1课件(14张PPT)
文档属性
| 名称 | 2.5夹角的计算-北师大版高中数学选修2-1课件(14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 899.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览

文档简介
立体几何中的向量方法
——夹角问题
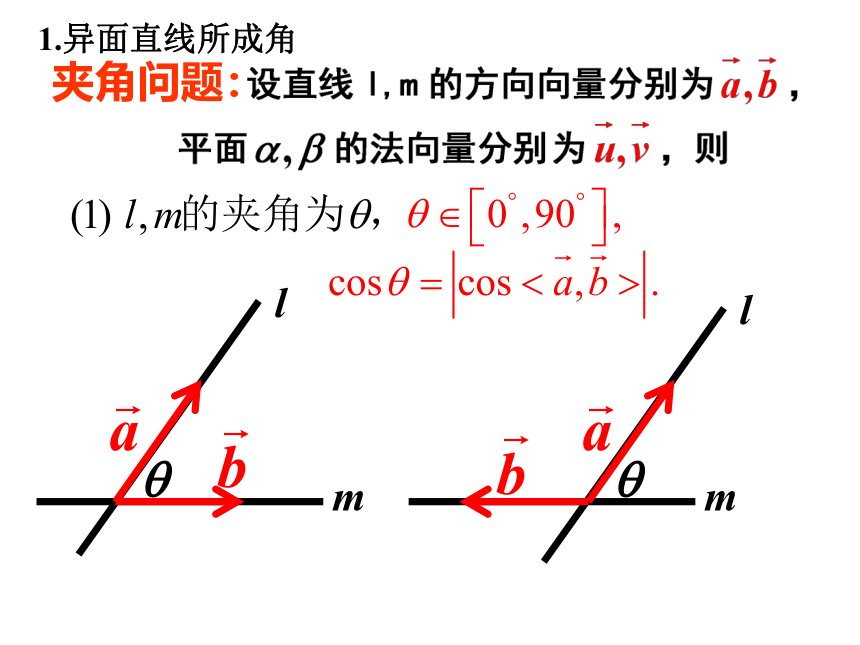
夹角问题:
l
m
l
m
1.异面直线所成角
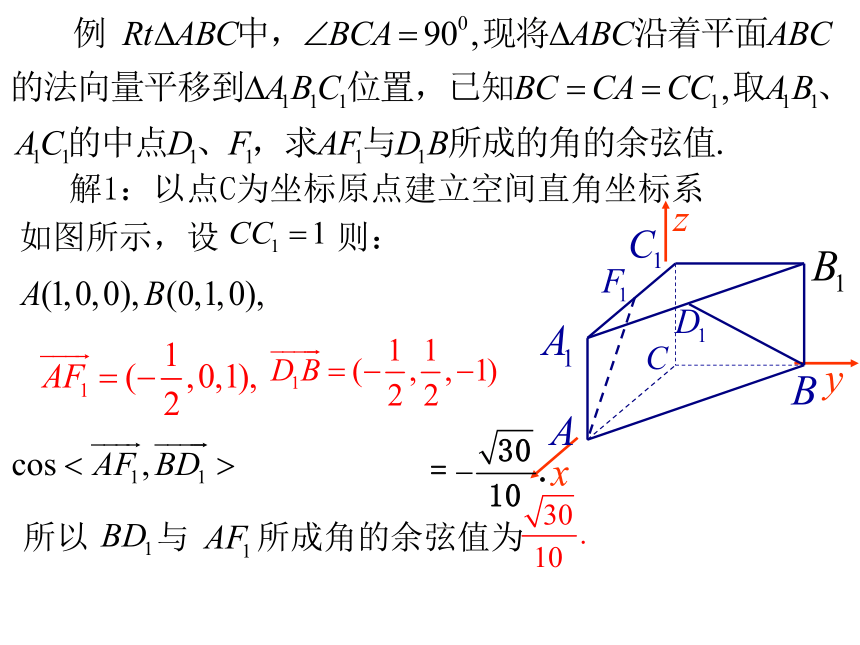
解1:以点C为坐标原点建立空间直角坐标系 如图所示,设 则:
所以 与 所成角的余弦值为
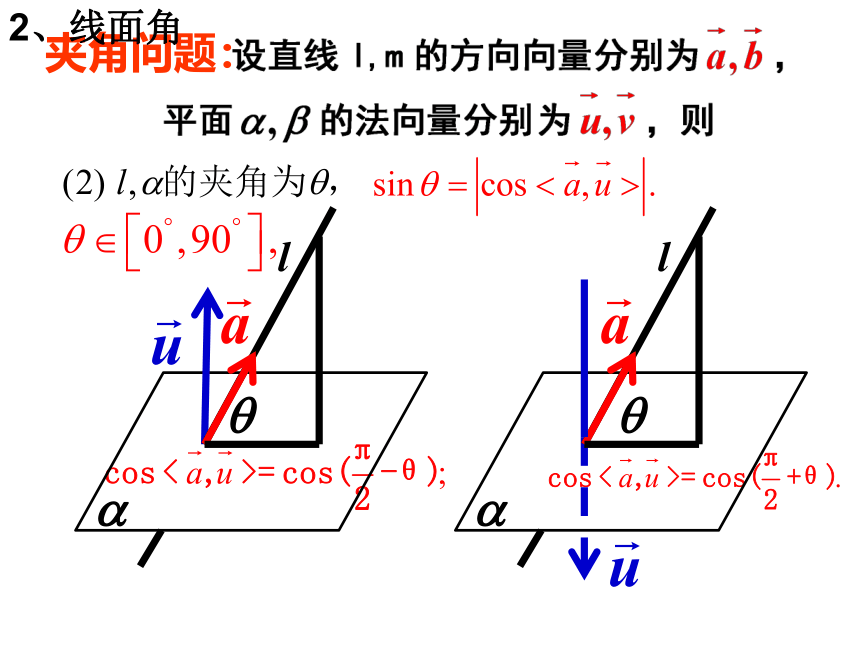
夹角问题:
l
l
2、线面角
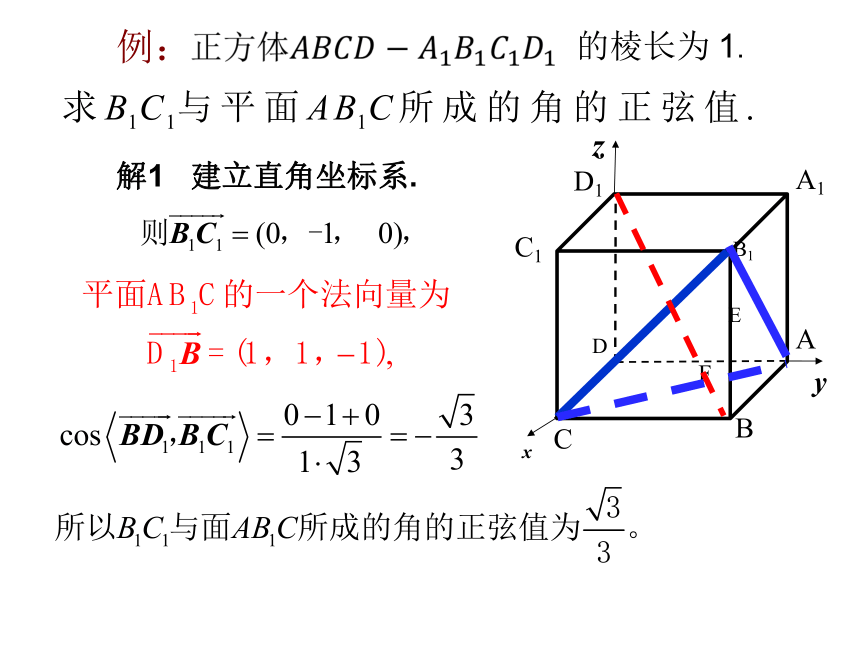
例:
的棱长为 1.
解1 建立直角坐标系.
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
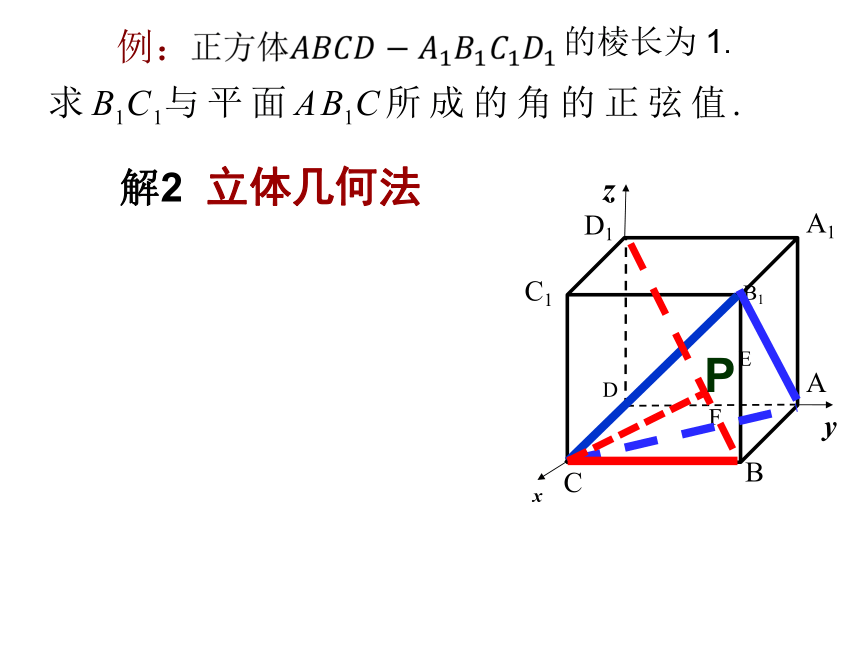
例:
的棱长为 1.
解2 立体几何法
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
P
解2 立体几何法
夹角问题:
P
P’
A
l
3、二面角
3、二面角
注意法向量的方向:同进同出,二面角等于法向量夹角的补角;一进一出,二面角等于法向量夹角
3、二面角
例4 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D
的大小。
A
B
C
D
P
E
F
X
Y
Z
平面PBC的一个法向量为:
解 如图所示建立
空间直角坐标系,设DC=1.
平面PBD的一个法向量为:
G
例4 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D的大小。
A
B
C
D
P
E
F
解2 立体几何法:设DC=1,
练习
的棱长为 1.
解1 建立直角坐标系.
A1
x
D1
B1
A
D
B
C
C1
y
z
平面ABD1的一个法向量为
平面CBD1的一个法向量为
的棱长为 1.
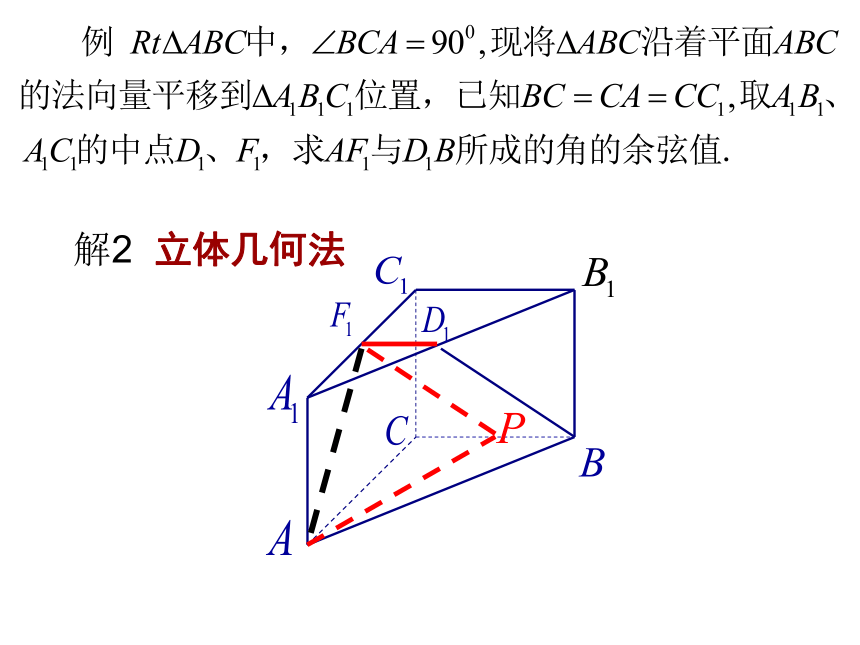
解2 立体几何法
A1
D1
B1
A
D
B
C
C1
P
——夹角问题
夹角问题:
l
m
l
m
1.异面直线所成角
解1:以点C为坐标原点建立空间直角坐标系 如图所示,设 则:
所以 与 所成角的余弦值为
夹角问题:
l
l
2、线面角
例:
的棱长为 1.
解1 建立直角坐标系.
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
例:
的棱长为 1.
解2 立体几何法
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
P
解2 立体几何法
夹角问题:
P
P’
A
l
3、二面角
3、二面角
注意法向量的方向:同进同出,二面角等于法向量夹角的补角;一进一出,二面角等于法向量夹角
3、二面角
例4 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D
的大小。
A
B
C
D
P
E
F
X
Y
Z
平面PBC的一个法向量为:
解 如图所示建立
空间直角坐标系,设DC=1.
平面PBD的一个法向量为:
G
例4 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D的大小。
A
B
C
D
P
E
F
解2 立体几何法:设DC=1,
练习
的棱长为 1.
解1 建立直角坐标系.
A1
x
D1
B1
A
D
B
C
C1
y
z
平面ABD1的一个法向量为
平面CBD1的一个法向量为
的棱长为 1.
解2 立体几何法
A1
D1
B1
A
D
B
C
C1
P
同课章节目录
