3.1.1椭圆及其标准方程-北师大版高中数学选修2-1课件(37张PPT)
文档属性
| 名称 | 3.1.1椭圆及其标准方程-北师大版高中数学选修2-1课件(37张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 09:57:02 | ||
图片预览










文档简介
3.1.1 椭圆及其标准方程
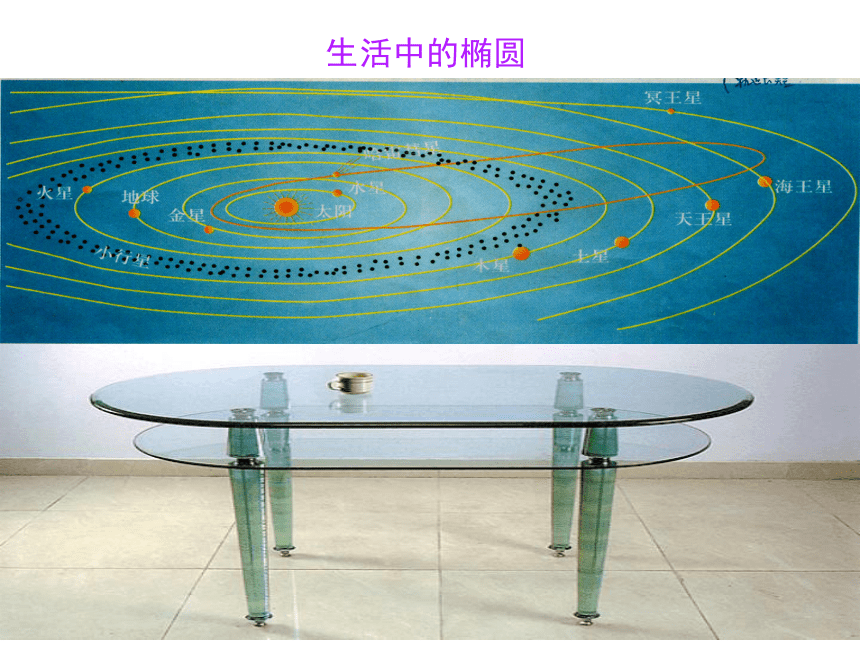
生活中的椭圆
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
(二)突出认知、建构概念
一、合作探究,形成概念:
1.取一条定长的细绳,把它的两端都固定在图板的同一点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个什么图形?笔尖(动点)满足什么几何条件?
2.如果把细绳的两端拉开一段距离,分别固定在图板的两点处,套上铅笔,拉紧绳子,移动笔尖,画出的又是什么图形?这一过程中,笔尖(动点)满足什么几何条件?
请同学们用事先准备好的学习用具小组内共同完成一下任务,并思考相应问题。
思考
数学实验
(1)取一条细绳,
(2)把它的两端固定在板上的两个定点F1、F2
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的 图形
1.在椭圆形成的过程中,细绳的两端的位置是固定的还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明了什么?
3.在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系?
1. 椭圆定义:
平面内与两个定点 的距离的和等于常数(大于
)的点的轨迹叫作椭圆。这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 。
|MF1|+|MF2|=2a
M
F1
F2
记焦距为2c,椭圆上的点M与F1, F2的距离和记为2a。
(|F1F2|=2c,
(三)注重本质 、理解概念
2a>2c>0)
绳长等于两定点间
距离即2a=2c 时,
绳长小于两定点间
距离即2a<2c时,
M
F1
F2
F1
F2
思考
为什么要求
(三)注重本质、理解概念
轨迹为线段;
无轨迹。
注意:椭圆定义中的关键点:
(1)距离的和2a 大于焦距2c ,即2a>2c>0.
(2) 平面内. ---这是大前提
(3)动点M与两定点 的距离的和等于常数2a.
1. 椭圆定义:
平面内与两个定点 的距离的和等于常数(大于
)的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .
|MF1|+|MF2|=2a (2a>2c>0, |F1F2|=2c)
M
F1
F2
记焦距为2c,椭圆上的点M与F1, F2的距离的和记为2a。
(三)注重本质、理解概念
求曲线方程的步骤是什么?
(1)建立适当的坐标系,设曲线上任意一点M的坐标为(x,y);
(2)找出限制条件 p(M);
(3)把坐标代入限制条件p(M) ,列出方程 f (x,y)=0;
(4)化简方程 f (x,y)=0;
(5)检验(可以省略,如有特殊情况,适当说明)
建、 设、限、代、化
结合椭圆的几何特征,你认为怎样选择坐标系才能使椭圆的方程简单?
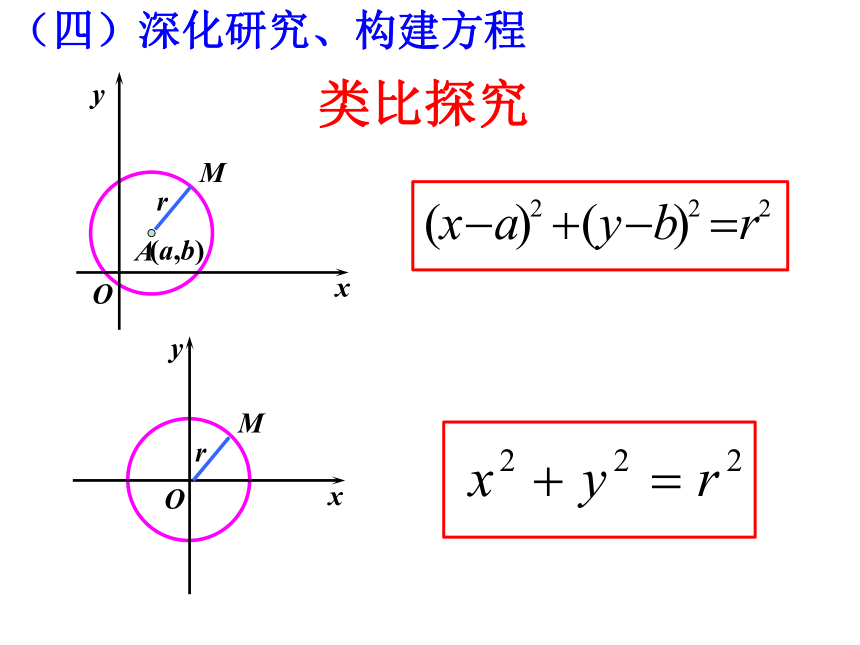
(四)深化研究、构建方程
x
O
y
A
(a,b)
M
r
x
O
y
M
r
类比探究
(四)深化研究、构建方程
建立平面直角坐标系一般遵循的原则:对称、简洁
x
O
y
M
方案一
? 探讨建立平面直角坐标系的方案
(四)深化研究、构建方程
方案二
x
O
y
以F1、F2 所在直线为 x 轴,线段 F1F2的垂直平分线为 y 轴建立直角坐标系.
由椭圆定义可知
化
代
设
建
F1
F2
x
y
M( x , y )
设 M( x,y )是椭圆上任意一点,
椭圆的焦距为2c,则有F1(-c,0)、F2(c,0).
则:
O
椭圆标准方程的推导
限
限制条件为:
两边同除以 得
(四)深化研究、构建方程
又设M与F1, F2的距离的和等于2a
F1
F2
x
y
M( x , y )
椭圆的标准方程
(四)深化研究、构建方程
焦点在 轴上
思考:
焦点在 轴上的方程是什么?
O
x
y
焦点在y轴:
焦点在x轴:
1
o
F
y
x
2
F
M( x , y )
1
2
y
o
F
F
M( x , y )
x
椭圆的标准方程
(四)深化研究、构建方程
Y型椭圆
X型椭圆
由两点间的距离公式,可知:
设|F1F2|=2c(c>0),M(x,y)为椭圆上任意一点,则有F1(0,-c),F2(0,c),
又由椭圆 的定义可得:
|MF1|+ |MF2|=2a
(请大家比较一下上面两式的不同,独立思考后回答椭圆的标准方程。)
焦点在Y轴
焦点在X轴
焦点在x轴上的标准方程:
焦点在y轴上的标准方程:
如果已知椭圆的标准方程,如何确定焦点在哪条坐标轴上?
(1)焦点在x轴的椭圆,x2项分母较大.
(2)焦点在y轴的椭圆,y2 项分母较大.
O
X
Y
F1
F2
M
(-c,0)
(c,0)
Y
X
O
F1
F2
M
(0,-c)
(0 , c)
椭圆的标准方程的认识:
(1)“椭圆的标准方程”是个专有名词,专指本节介绍的两
个方程,方程形式是固定的。
(3)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。
(4)由椭圆的标准方程可以求出三个参数a、b、c的值。
(2)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪
一个轴上,即“椭圆的焦点看分母,谁大在谁上”
则方程可化为
观察左图, 和同桌讨论你们能从中找出表示c 、 a 的线段吗?
a2-c2 有什么几何意义?
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
练习:下列方程哪些表示椭圆?若表示椭圆焦点在那个轴上?(独立思考后回答)
例1、填空:(独立思考后回答)
(1)已知椭圆的方程为: ,则
a=_____,b=_______,c=_______,
焦点坐标为: ,焦距
等于_____;
若曲线上一点P到左焦点F1的距离为3,则
点P到另一个焦点F2的距离等于_________,
则?F1PF2的周长为___________
2
1
(0,-1)、(0,1)
2
|PF1|+|PF2|=2a
三、迁移应用,能力提高
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
F1
F2
(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则?F2CD的周长为________
5
4
3
(3,0)、(-3,0)
6
20
F1
F2
C
D
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
|CF1|+|CF2|=2a
(3)a=5,c=4的椭圆标准方程是
。
或
练习1:判定下列椭圆的焦点在哪条轴上?并指明a2、b2,写出焦点坐标
答:在 X 轴。(-3,0)和
(3,0)
答:在 y 轴。(0,-5)和
(0,5)
答:在y 轴。(0,-1)和
(0,1)
练习2:将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标
解:因为椭圆的焦点在 轴上,设
由椭圆的定义知
所以
又因为 , 所以
因此,所求椭圆的标准方程为
定义法
x
F1
F2
P
O
y
(六)应用拓展、提高能力
已知椭圆两个焦点的坐标分别是( -2, 0 ), (2,0), 并且经过点P ,求它的标准方程.
例1:
解:因为椭圆的焦点在 轴上,设
由于 所以
①
又点 在椭圆上
②
联立方程①②解得
因此所求椭圆的标准方程为
x
F1
F2
P
O
y
待定系数法
已知椭圆两个焦点的坐标分别是( -2, 0 ), (2,0), 并且经过点P ,求它的标准方程.
例1:
(六)应用拓展、提高能力
例2、如图,在圆 上任取一点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
解:设点M坐标为M(x,y), 点P的坐标为
P(x’,y’),则
由题意可得:
因为
所以
即
这就是点M的轨迹方程,它表示一个椭圆。
相关点分析法:即利用中间变量求曲线方程.
o
x
y
P
M
D
例3 设点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是-4/9,求点M的轨迹方程。
“杂点”可不要忘了哟
注:①这样设不失为一种方法.
y
o
F
1
F
2
x
例4.已知椭圆 ,焦点为F1和F2 ,P是椭圆
上一点,且 ,求 的周长和面积。
通常叫做焦点三角形,其周长为定值2a + 2c.
相关知识:
注意新旧知识的综合运用
通常叫做焦点三角形,其周长为定值2a + 2c,
其面积为
(七)回顾反思、提升经验
一个概念:
两个方程:
两种方法:
三个意识:
|MF1|+|MF2|=2a (2a>2c>0)
定义法;待定系数法.
类比意识;求美意识;求简意识.
两种思想:
数形结合的思想;坐标法的思想.
标准方程中,分母哪个大,焦点就在哪个轴上!
标 准 方 程
相 同 点
焦点位置的判断
不 同 点
图 形
焦 点 坐 标
a、b、c 的关系
焦点在x轴上
焦点在y轴上
y
x
M
O
F1
F2
生活中的椭圆
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
(二)突出认知、建构概念
一、合作探究,形成概念:
1.取一条定长的细绳,把它的两端都固定在图板的同一点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个什么图形?笔尖(动点)满足什么几何条件?
2.如果把细绳的两端拉开一段距离,分别固定在图板的两点处,套上铅笔,拉紧绳子,移动笔尖,画出的又是什么图形?这一过程中,笔尖(动点)满足什么几何条件?
请同学们用事先准备好的学习用具小组内共同完成一下任务,并思考相应问题。
思考
数学实验
(1)取一条细绳,
(2)把它的两端固定在板上的两个定点F1、F2
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的 图形
1.在椭圆形成的过程中,细绳的两端的位置是固定的还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明了什么?
3.在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系?
1. 椭圆定义:
平面内与两个定点 的距离的和等于常数(大于
)的点的轨迹叫作椭圆。这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 。
|MF1|+|MF2|=2a
M
F1
F2
记焦距为2c,椭圆上的点M与F1, F2的距离和记为2a。
(|F1F2|=2c,
(三)注重本质 、理解概念
2a>2c>0)
绳长等于两定点间
距离即2a=2c 时,
绳长小于两定点间
距离即2a<2c时,
M
F1
F2
F1
F2
思考
为什么要求
(三)注重本质、理解概念
轨迹为线段;
无轨迹。
注意:椭圆定义中的关键点:
(1)距离的和2a 大于焦距2c ,即2a>2c>0.
(2) 平面内. ---这是大前提
(3)动点M与两定点 的距离的和等于常数2a.
1. 椭圆定义:
平面内与两个定点 的距离的和等于常数(大于
)的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .
|MF1|+|MF2|=2a (2a>2c>0, |F1F2|=2c)
M
F1
F2
记焦距为2c,椭圆上的点M与F1, F2的距离的和记为2a。
(三)注重本质、理解概念
求曲线方程的步骤是什么?
(1)建立适当的坐标系,设曲线上任意一点M的坐标为(x,y);
(2)找出限制条件 p(M);
(3)把坐标代入限制条件p(M) ,列出方程 f (x,y)=0;
(4)化简方程 f (x,y)=0;
(5)检验(可以省略,如有特殊情况,适当说明)
建、 设、限、代、化
结合椭圆的几何特征,你认为怎样选择坐标系才能使椭圆的方程简单?
(四)深化研究、构建方程
x
O
y
A
(a,b)
M
r
x
O
y
M
r
类比探究
(四)深化研究、构建方程
建立平面直角坐标系一般遵循的原则:对称、简洁
x
O
y
M
方案一
? 探讨建立平面直角坐标系的方案
(四)深化研究、构建方程
方案二
x
O
y
以F1、F2 所在直线为 x 轴,线段 F1F2的垂直平分线为 y 轴建立直角坐标系.
由椭圆定义可知
化
代
设
建
F1
F2
x
y
M( x , y )
设 M( x,y )是椭圆上任意一点,
椭圆的焦距为2c,则有F1(-c,0)、F2(c,0).
则:
O
椭圆标准方程的推导
限
限制条件为:
两边同除以 得
(四)深化研究、构建方程
又设M与F1, F2的距离的和等于2a
F1
F2
x
y
M( x , y )
椭圆的标准方程
(四)深化研究、构建方程
焦点在 轴上
思考:
焦点在 轴上的方程是什么?
O
x
y
焦点在y轴:
焦点在x轴:
1
o
F
y
x
2
F
M( x , y )
1
2
y
o
F
F
M( x , y )
x
椭圆的标准方程
(四)深化研究、构建方程
Y型椭圆
X型椭圆
由两点间的距离公式,可知:
设|F1F2|=2c(c>0),M(x,y)为椭圆上任意一点,则有F1(0,-c),F2(0,c),
又由椭圆 的定义可得:
|MF1|+ |MF2|=2a
(请大家比较一下上面两式的不同,独立思考后回答椭圆的标准方程。)
焦点在Y轴
焦点在X轴
焦点在x轴上的标准方程:
焦点在y轴上的标准方程:
如果已知椭圆的标准方程,如何确定焦点在哪条坐标轴上?
(1)焦点在x轴的椭圆,x2项分母较大.
(2)焦点在y轴的椭圆,y2 项分母较大.
O
X
Y
F1
F2
M
(-c,0)
(c,0)
Y
X
O
F1
F2
M
(0,-c)
(0 , c)
椭圆的标准方程的认识:
(1)“椭圆的标准方程”是个专有名词,专指本节介绍的两
个方程,方程形式是固定的。
(3)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。
(4)由椭圆的标准方程可以求出三个参数a、b、c的值。
(2)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪
一个轴上,即“椭圆的焦点看分母,谁大在谁上”
则方程可化为
观察左图, 和同桌讨论你们能从中找出表示c 、 a 的线段吗?
a2-c2 有什么几何意义?
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
练习:下列方程哪些表示椭圆?若表示椭圆焦点在那个轴上?(独立思考后回答)
例1、填空:(独立思考后回答)
(1)已知椭圆的方程为: ,则
a=_____,b=_______,c=_______,
焦点坐标为: ,焦距
等于_____;
若曲线上一点P到左焦点F1的距离为3,则
点P到另一个焦点F2的距离等于_________,
则?F1PF2的周长为___________
2
1
(0,-1)、(0,1)
2
|PF1|+|PF2|=2a
三、迁移应用,能力提高
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
F1
F2
(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则?F2CD的周长为________
5
4
3
(3,0)、(-3,0)
6
20
F1
F2
C
D
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
|CF1|+|CF2|=2a
(3)a=5,c=4的椭圆标准方程是
。
或
练习1:判定下列椭圆的焦点在哪条轴上?并指明a2、b2,写出焦点坐标
答:在 X 轴。(-3,0)和
(3,0)
答:在 y 轴。(0,-5)和
(0,5)
答:在y 轴。(0,-1)和
(0,1)
练习2:将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标
解:因为椭圆的焦点在 轴上,设
由椭圆的定义知
所以
又因为 , 所以
因此,所求椭圆的标准方程为
定义法
x
F1
F2
P
O
y
(六)应用拓展、提高能力
已知椭圆两个焦点的坐标分别是( -2, 0 ), (2,0), 并且经过点P ,求它的标准方程.
例1:
解:因为椭圆的焦点在 轴上,设
由于 所以
①
又点 在椭圆上
②
联立方程①②解得
因此所求椭圆的标准方程为
x
F1
F2
P
O
y
待定系数法
已知椭圆两个焦点的坐标分别是( -2, 0 ), (2,0), 并且经过点P ,求它的标准方程.
例1:
(六)应用拓展、提高能力
例2、如图,在圆 上任取一点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
解:设点M坐标为M(x,y), 点P的坐标为
P(x’,y’),则
由题意可得:
因为
所以
即
这就是点M的轨迹方程,它表示一个椭圆。
相关点分析法:即利用中间变量求曲线方程.
o
x
y
P
M
D
例3 设点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是-4/9,求点M的轨迹方程。
“杂点”可不要忘了哟
注:①这样设不失为一种方法.
y
o
F
1
F
2
x
例4.已知椭圆 ,焦点为F1和F2 ,P是椭圆
上一点,且 ,求 的周长和面积。
通常叫做焦点三角形,其周长为定值2a + 2c.
相关知识:
注意新旧知识的综合运用
通常叫做焦点三角形,其周长为定值2a + 2c,
其面积为
(七)回顾反思、提升经验
一个概念:
两个方程:
两种方法:
三个意识:
|MF1|+|MF2|=2a (2a>2c>0)
定义法;待定系数法.
类比意识;求美意识;求简意识.
两种思想:
数形结合的思想;坐标法的思想.
标准方程中,分母哪个大,焦点就在哪个轴上!
标 准 方 程
相 同 点
焦点位置的判断
不 同 点
图 形
焦 点 坐 标
a、b、c 的关系
焦点在x轴上
焦点在y轴上
y
x
M
O
F1
F2
同课章节目录
