3.3.1双曲线及其标准方程-北师大版高中数学选修2-1课件(24张PPT)
文档属性
| 名称 | 3.3.1双曲线及其标准方程-北师大版高中数学选修2-1课件(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 10:00:52 | ||
图片预览





文档简介
3.3.1双曲线及其
标准方程
*
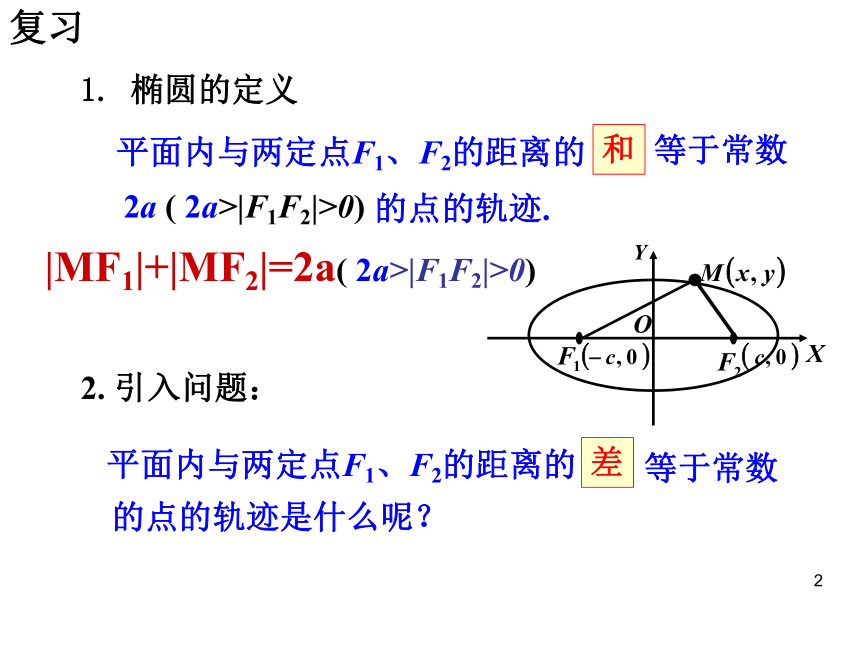
1. 椭圆的定义
和
等于常数
2a ( 2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2. 引入问题:
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
复习
|MF1|+|MF2|=2a( 2a>|F1F2|>0)
*
①如图(A),
|MF1|-|MF2|=|F2F|=2a
②如图(B),
上面 两条合起来叫做双曲线
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
|MF2|-|MF1|=|F1F|=2a
*
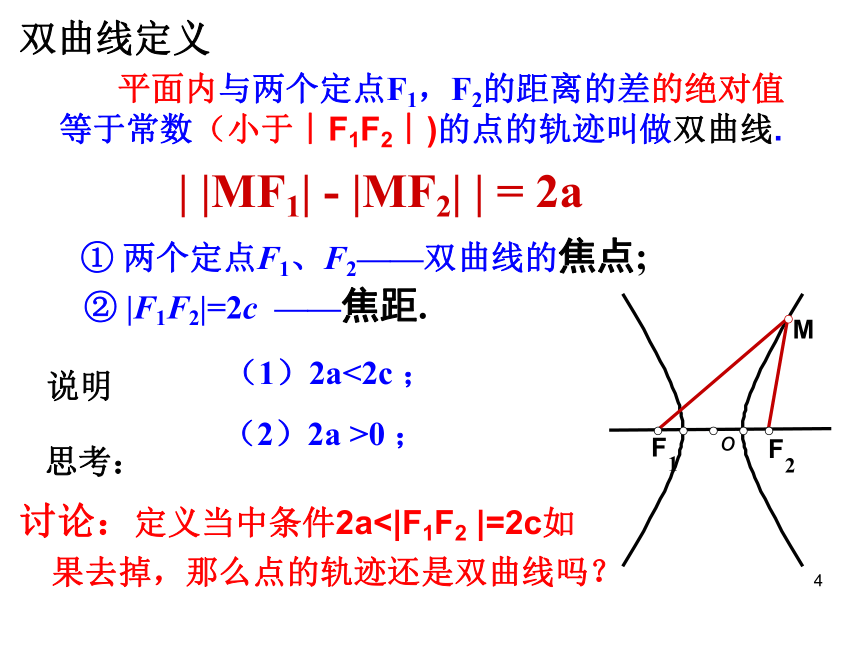
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
(1)2a<2c ;
o
F
2
F
1
M
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于︱F1F2︱)的点的轨迹叫做双曲线.
(2)2a >0 ;
双曲线定义
思考:
说明
| |MF1| - |MF2| | = 2a
*
讨论:定义当中条件2a<|F1F2 |=2c如果去掉,那么点的轨迹还是双曲线吗?
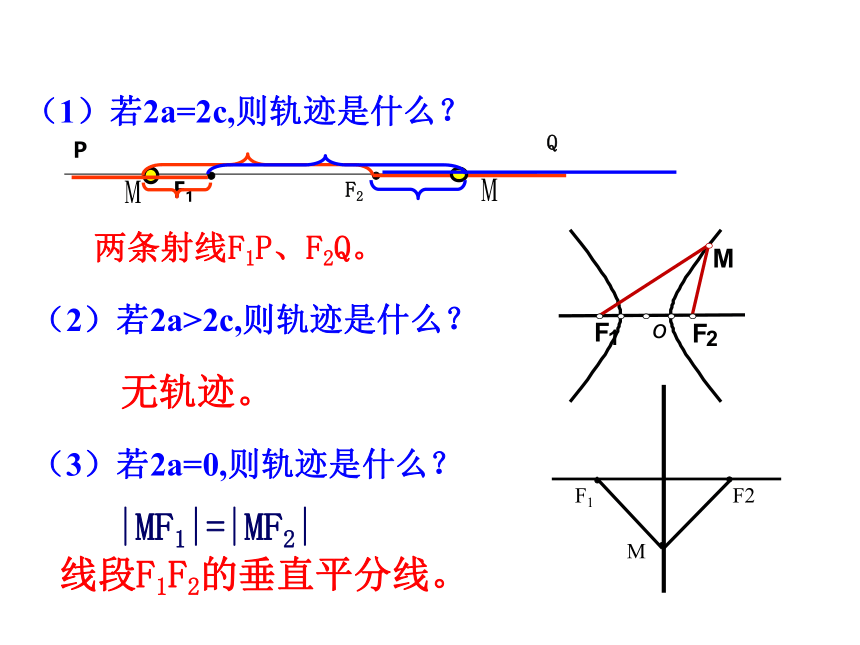
两条射线F1P、F2Q。
F2
F1
P
M
Q
M
无轨迹。
线段F1F2的垂直平分线。
|MF1|=|MF2|
F1
F2
M
o
F
2
F
1
M
(1)若2a=2c,则轨迹是什么?
(2)若2a>2c,则轨迹是什么?
(3)若2a=0,则轨迹是什么?
1、当||MF1|-|MF2||= 2a<|F1F2|时,
2、当 ||MF1|-|MF2||= 2a=|F1F2|时,
3、当||MF1|-|MF2||= 2a >|F1F2|时,M点的轨迹不存在
4、当||MF1|-|MF2||= 2a=0时,
M点轨迹是双曲线
其中当|MF1|-|MF2|= 2a时,M点轨迹是双曲线中靠近F2的一支; 当|MF2| - |MF1|= 2a时,M点轨迹是双曲线中靠近F1的一支.
M点轨迹是在直
线F1F2上且以F1和F2为端点向外的两条射线。
M点的轨迹是线段F1F2
的垂直平分线 。
结论:
5. M在右支上 |MF1|-|MF2| =2a
M在左支上 |MF1|-|MF2|= - 2a
*
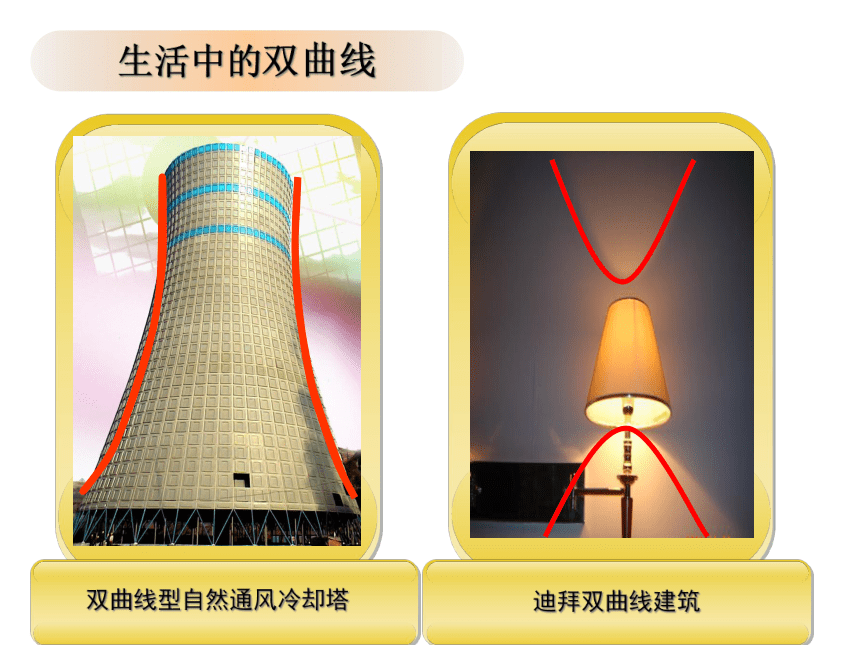
迪拜双曲线建筑
生活中的双曲线
双曲线型自然通风冷却塔
生活中的双曲线
可口可乐的下半部
玉枕的形状
生活中的双曲线
生活中的双曲线
F
2
F
1
M
x
O
y
求曲线方程的步骤:
双曲线的标准方程
1. 建系.
以F1,F2所在的直线为x轴,线段F1F2的中点为原点建立直角坐标系
2.设点.
设M(x , y),则F1(-c,0),F2(c,0)
3.列式
|MF1| - |MF2|=±2a
4.化简
*
此即为焦点在x轴上的双曲线的标准方程
*
F
2
F
1
M
x
O
y
O
M
F2
F1
x
y
若建系时,焦点在y轴上呢?
*
看 前的系数,哪一个为正,则在哪一个轴上
2、双曲线的标准方程与椭圆的标准方程有何区别与联系?
1、如何判断双曲线的焦点在哪个轴上?
问题
*
定 义
方 程
焦 点
a.b.c的关系
F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭 圆
双曲线
F(0,±c)
F(0,±c)
*
双曲线的标准方程:
椭圆的标准方程:
*
*
*
*
例2.已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,求动圆圆心M的轨迹方程.
解:设动圆M与圆C1及圆C2分别外切于点A
和B,根据两圆外切的条件,
|MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|
这表明动点M与两定点C2、C1的距离的差是常数2.根
据双曲线的定义,动点M的轨迹为双曲线的左支(点M与C2
的距离大,与C1的距离小),这里a=1,c=3,则b2=8,设点M
的坐标为(x,y),其轨迹方程为:
变式训练: 已知B(-5,0),C(5,0)是三角形ABC的两个顶点,且
求顶点A的轨迹方程。
解:在△ABC中,|BC|=10,
故顶点A的轨迹是以B、C为焦点的双曲线的左支
又因c=5,a=3,则b=4
则顶点A的轨迹方程为
例3:如果方程 表示双曲线,求m的取值范围.
解:
方程 表示焦点在y轴双曲线时,
则m的取值范围_____________.
思考:
课堂练习
1、a=4,b=3 ,焦点在x轴上的双曲线的标准方程是
3、设双曲线 上的点P到(5,0)的距离是15,则P到
(-5,0)的距离是 .
7或23
4、如果方程 表示双曲线,则m的取值范围
是 __________
2、焦点为(0, -6),(0,6),经过点(2,-5)的双曲线的标 准方程是
m | m>-1或m< -2
知识迁移 深化认知
(3)应用
(1)定义:
| |MF1|-|MF2| | =2a(0<2a<|F1F2|)
由方程定焦点:椭 圆看大小
双曲线看符号
知识迁移 深化认知
标准方程
*
1. 椭圆的定义
和
等于常数
2a ( 2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2. 引入问题:
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
复习
|MF1|+|MF2|=2a( 2a>|F1F2|>0)
*
①如图(A),
|MF1|-|MF2|=|F2F|=2a
②如图(B),
上面 两条合起来叫做双曲线
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
|MF2|-|MF1|=|F1F|=2a
*
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
(1)2a<2c ;
o
F
2
F
1
M
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于︱F1F2︱)的点的轨迹叫做双曲线.
(2)2a >0 ;
双曲线定义
思考:
说明
| |MF1| - |MF2| | = 2a
*
讨论:定义当中条件2a<|F1F2 |=2c如果去掉,那么点的轨迹还是双曲线吗?
两条射线F1P、F2Q。
F2
F1
P
M
Q
M
无轨迹。
线段F1F2的垂直平分线。
|MF1|=|MF2|
F1
F2
M
o
F
2
F
1
M
(1)若2a=2c,则轨迹是什么?
(2)若2a>2c,则轨迹是什么?
(3)若2a=0,则轨迹是什么?
1、当||MF1|-|MF2||= 2a<|F1F2|时,
2、当 ||MF1|-|MF2||= 2a=|F1F2|时,
3、当||MF1|-|MF2||= 2a >|F1F2|时,M点的轨迹不存在
4、当||MF1|-|MF2||= 2a=0时,
M点轨迹是双曲线
其中当|MF1|-|MF2|= 2a时,M点轨迹是双曲线中靠近F2的一支; 当|MF2| - |MF1|= 2a时,M点轨迹是双曲线中靠近F1的一支.
M点轨迹是在直
线F1F2上且以F1和F2为端点向外的两条射线。
M点的轨迹是线段F1F2
的垂直平分线 。
结论:
5. M在右支上 |MF1|-|MF2| =2a
M在左支上 |MF1|-|MF2|= - 2a
*
迪拜双曲线建筑
生活中的双曲线
双曲线型自然通风冷却塔
生活中的双曲线
可口可乐的下半部
玉枕的形状
生活中的双曲线
生活中的双曲线
F
2
F
1
M
x
O
y
求曲线方程的步骤:
双曲线的标准方程
1. 建系.
以F1,F2所在的直线为x轴,线段F1F2的中点为原点建立直角坐标系
2.设点.
设M(x , y),则F1(-c,0),F2(c,0)
3.列式
|MF1| - |MF2|=±2a
4.化简
*
此即为焦点在x轴上的双曲线的标准方程
*
F
2
F
1
M
x
O
y
O
M
F2
F1
x
y
若建系时,焦点在y轴上呢?
*
看 前的系数,哪一个为正,则在哪一个轴上
2、双曲线的标准方程与椭圆的标准方程有何区别与联系?
1、如何判断双曲线的焦点在哪个轴上?
问题
*
定 义
方 程
焦 点
a.b.c的关系
F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭 圆
双曲线
F(0,±c)
F(0,±c)
*
双曲线的标准方程:
椭圆的标准方程:
*
*
*
*
例2.已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,求动圆圆心M的轨迹方程.
解:设动圆M与圆C1及圆C2分别外切于点A
和B,根据两圆外切的条件,
|MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|
这表明动点M与两定点C2、C1的距离的差是常数2.根
据双曲线的定义,动点M的轨迹为双曲线的左支(点M与C2
的距离大,与C1的距离小),这里a=1,c=3,则b2=8,设点M
的坐标为(x,y),其轨迹方程为:
变式训练: 已知B(-5,0),C(5,0)是三角形ABC的两个顶点,且
求顶点A的轨迹方程。
解:在△ABC中,|BC|=10,
故顶点A的轨迹是以B、C为焦点的双曲线的左支
又因c=5,a=3,则b=4
则顶点A的轨迹方程为
例3:如果方程 表示双曲线,求m的取值范围.
解:
方程 表示焦点在y轴双曲线时,
则m的取值范围_____________.
思考:
课堂练习
1、a=4,b=3 ,焦点在x轴上的双曲线的标准方程是
3、设双曲线 上的点P到(5,0)的距离是15,则P到
(-5,0)的距离是 .
7或23
4、如果方程 表示双曲线,则m的取值范围
是 __________
2、焦点为(0, -6),(0,6),经过点(2,-5)的双曲线的标 准方程是
m | m>-1或m< -2
知识迁移 深化认知
(3)应用
(1)定义:
| |MF1|-|MF2| | =2a(0<2a<|F1F2|)
由方程定焦点:椭 圆看大小
双曲线看符号
知识迁移 深化认知
同课章节目录
