北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件(13张PPT)
文档属性
| 名称 | 北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件(13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 694.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览





文档简介
利用函数性质判定
方程解的存在
引例:
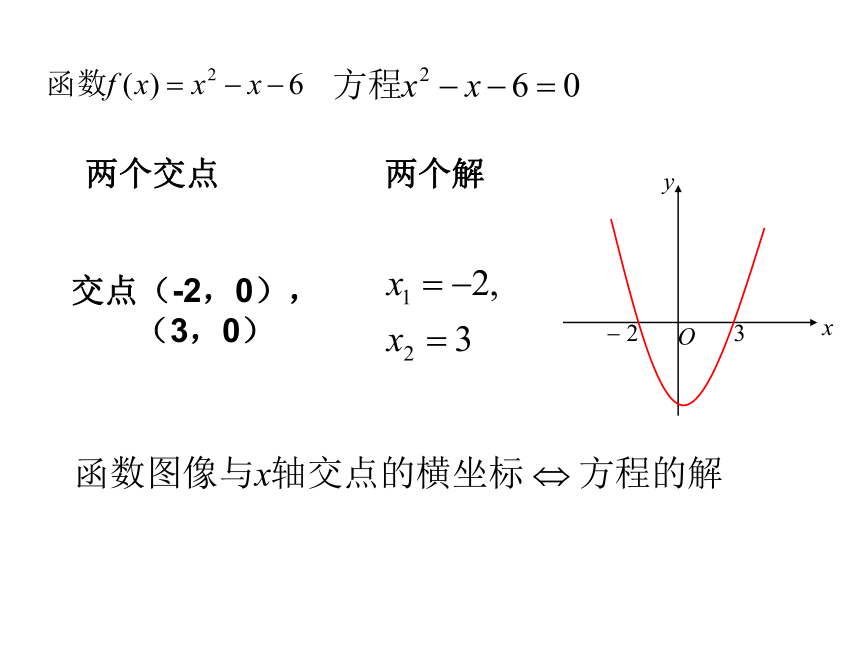
两个交点
两个解
交点(-2,0),
(3,0)
思考:
注:函数的零点个数就决定了相应方程实数解的个数
(1)
,
(2)
探究一:
- 6
6
<
有
探究二:
思考:
定理再加上什么条件就“有且只有一个零点”呢?
函数在区间上单调
定理只能说明存在零点,但不能确定零点的个数
思考:
定理的作用:
判定函数零点的存在,判定函数零点所在区间
例1
练习:
课堂小结:
1. 函数零点的概念;
3.数学思想:由特殊到一般,数形结合,函数与方程
2. 函数在某区间上存在零点的判定方法 .
作业:
课堂作业:P119 A组第1题;
课外探究:预习下一节,
方程解的存在
引例:
两个交点
两个解
交点(-2,0),
(3,0)
思考:
注:函数的零点个数就决定了相应方程实数解的个数
(1)
,
(2)
探究一:
- 6
6
<
有
探究二:
思考:
定理再加上什么条件就“有且只有一个零点”呢?
函数在区间上单调
定理只能说明存在零点,但不能确定零点的个数
思考:
定理的作用:
判定函数零点的存在,判定函数零点所在区间
例1
练习:
课堂小结:
1. 函数零点的概念;
3.数学思想:由特殊到一般,数形结合,函数与方程
2. 函数在某区间上存在零点的判定方法 .
作业:
课堂作业:P119 A组第1题;
课外探究:预习下一节,
