高二数学人教A版选修2-1课件:2.2.2椭圆的简单几何性质(55张PPT)
文档属性
| 名称 | 高二数学人教A版选修2-1课件:2.2.2椭圆的简单几何性质(55张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 17:13:36 | ||
图片预览






文档简介
(共55张PPT)
2.2.2 椭圆的简单几何性质
第1课时 椭圆的简单几何性质
1、掌握椭圆的简单几何性质;
2、理解离心率对椭圆扁平程度的影响.
重点:椭圆的简单几何性质.
难点:1、求椭圆的离心率;
2、常结合几何图形、方程、不等式、平面向
量等内容命题.
教学目标:
1、椭圆的范围:
2、椭圆的对称性:
3、椭圆的顶点:
4、椭圆的几何形状→扁平程度
变量x,y的取值范围
方程的对称性
x=0或y=0时方程的解
a,b,c
椭圆的性质:
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
椭圆的几何性质:
一、新课引入:
o
x
y
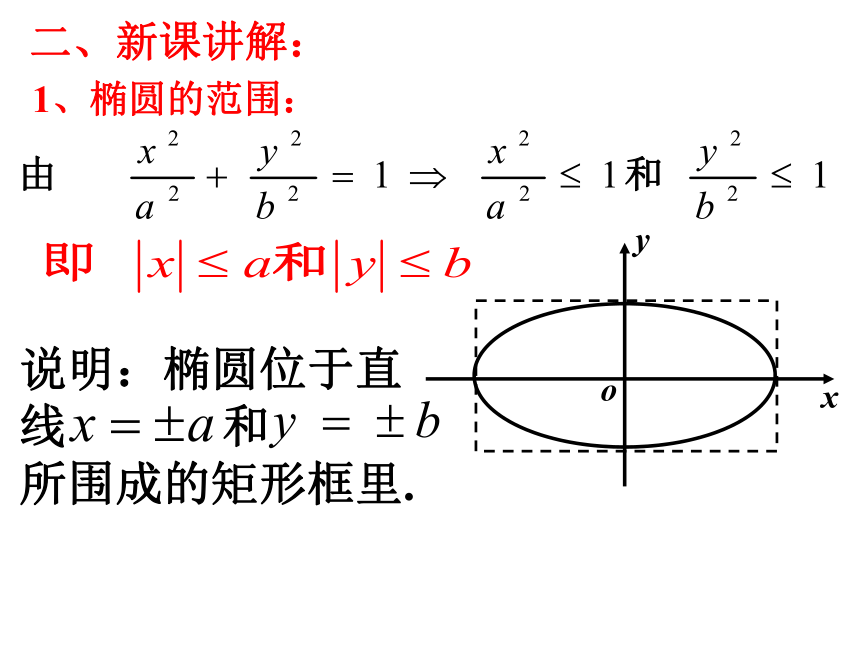
说明:椭圆位于直线 和 所围成的矩形框里.
二、新课讲解:
1、椭圆的范围:
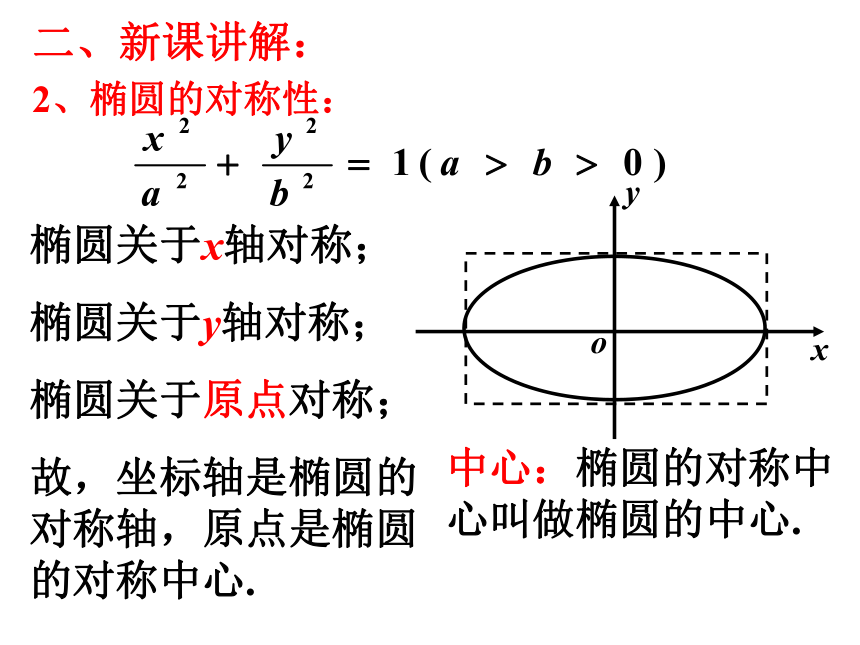
椭圆关于x轴对称;
椭圆关于y轴对称;
椭圆关于原点对称;
故,坐标轴是椭圆的对称轴,原点是椭圆的对称中心.
中心:椭圆的对称中心叫做椭圆的中心.
o
x
y
二、新课讲解:
2、椭圆的对称性:
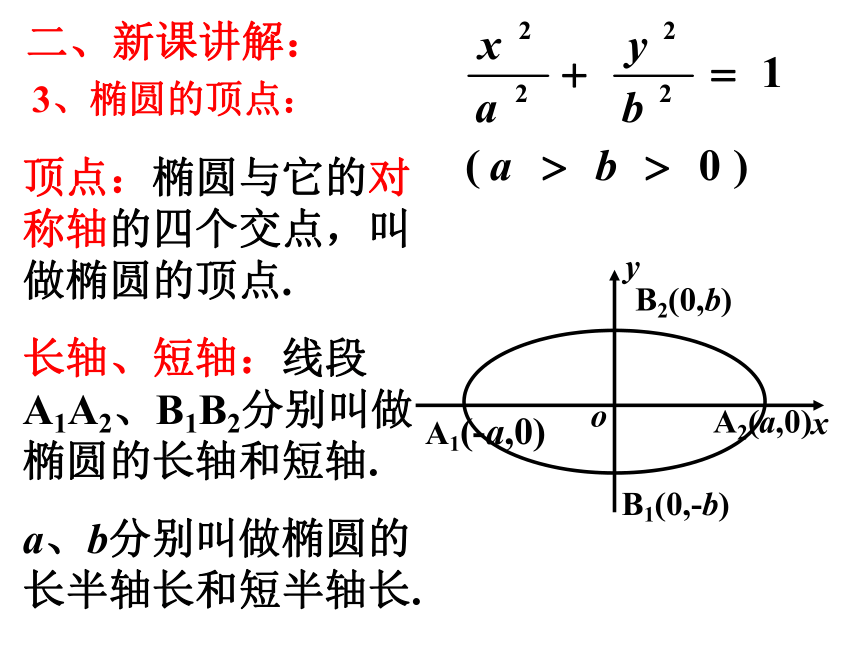
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点.
长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴.
a、b分别叫做椭圆的长半轴长和短半轴长.
o
x
y
B1(0,-b)
B2(0,b)
A1(-a,0)
A2(a,0)
二、新课讲解:
3、椭圆的顶点:
o
x
y
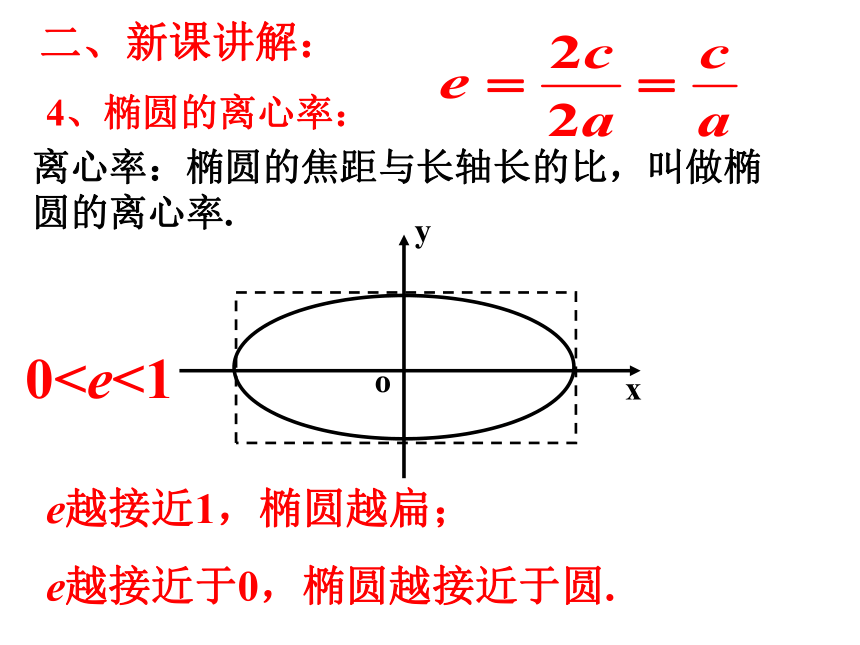
离心率:椭圆的焦距与长轴长的比,叫做椭圆的离心率.
0e越接近1,椭圆越扁;
e越接近于0,椭圆越接近于圆.
二、新课讲解:
4、椭圆的离心率:
b→0,e→1,椭圆越扁;
b→a,e→0,椭圆越接近于圆.
二、新课讲解:
4、椭圆的离心率:
用a和b表示椭圆的离心率e
二、新课讲解:
.
.
o
x
y
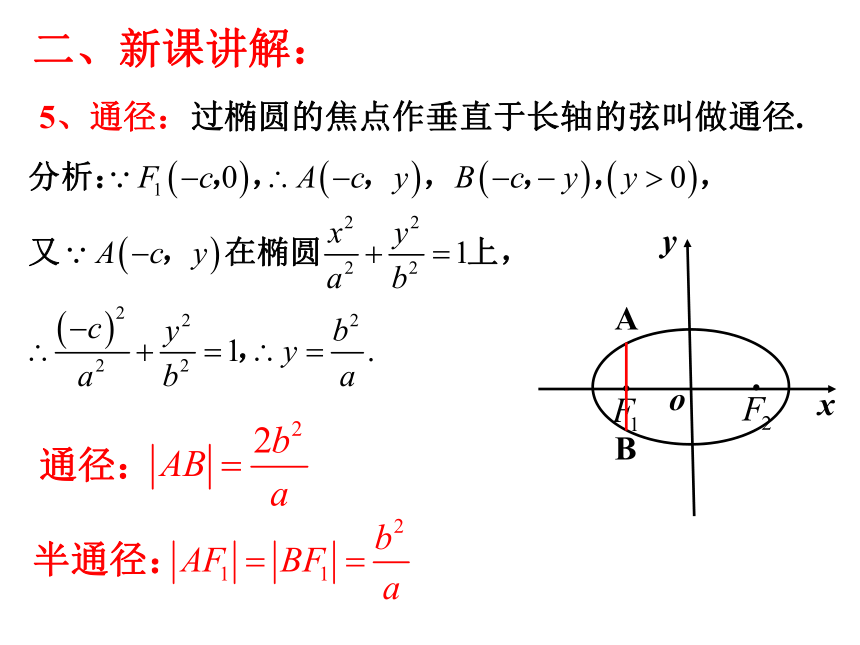
5、通径:过椭圆的焦点作垂直于长轴的弦叫做通径.
A
B
通径:
半通径:
二、新课讲解:
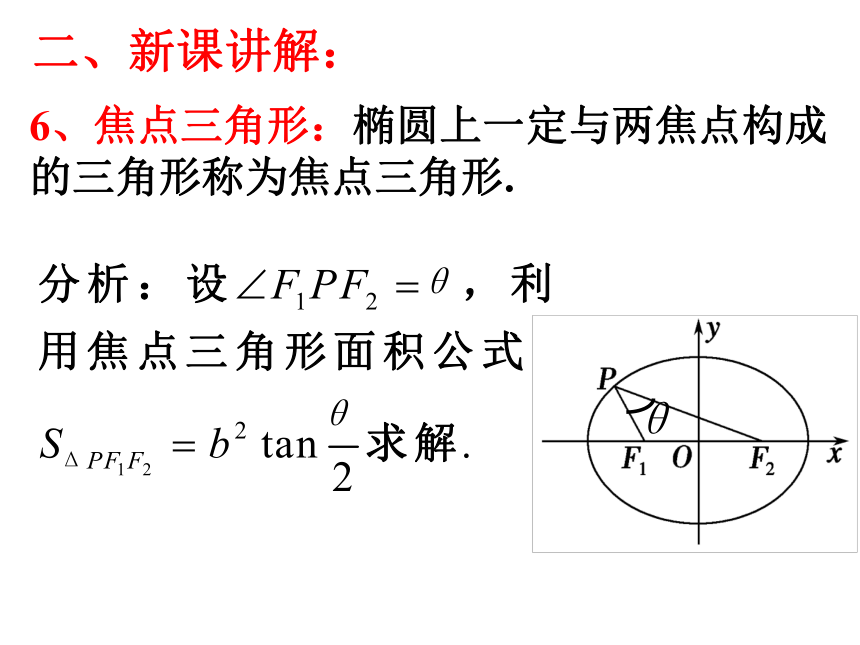
6、焦点三角形:椭圆上一定与两焦点构成的三角形称为焦点三角形.
所以,焦点三角形面积公式是:
焦点的位置 焦点在x轴上 焦点在y轴上
范围 __________
____________ __________
____________
顶点 ___________________
___________________ ___________________
___________________
轴长 短轴长=___,长轴长=___
焦点 ___________________ ___________________
焦距 |F1F2|=___
对称性 对称轴_________,对称中心______
离心率 e=_________
-a≤x≤a
且-b≤y≤b
-b≤x≤b
且-a≤y≤a
A1(-a,0)、A2(a,0)
B1(0,-b)、B2(0,b)
A1(0,-a)、A2(0,a)
B1(-b,0)、B2(b,0)
2b
2a
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
2c
x轴和y轴
(0,0)
椭圆的性质:
通径、焦点三角形面积公式
1、椭圆几何性质的应用:
(1)椭圆的焦点决定椭圆的位置,范围决定椭圆的大小,离心率决定了椭圆的扁圆程度,对称性是椭圆的重要特征,顶点是椭圆与对称轴的交点,是椭圆重要的特殊点;若已知椭圆的标准方程,则根据a、b的值可确定其性质.
(2)明确a,b的几何意义,a是长半轴长,b是短半轴长,不要与长轴长、短轴长混淆,由c2=a2-b2,可得“已知椭圆的四个顶点,求焦点”的几何作图法,只要以短轴的端点B1(或B2)为圆心,以a为半径作弧交长轴于两点,这两点就是焦点.
点评:
2、椭圆的离心率对椭圆形状的影响:
例4、椭圆16x2+25y2=400的长轴长为____,短轴长为____,焦点坐标为 ,顶点坐标为 , 离心率为
______.
8
10
三、例题分析:
例5、P40
三、例题分析:
M
.
d
o
x
y
.
l
图2.2-12
圆锥曲线的第二定义
三、例题分析:
.
.
o
x
y
图2.2-13
l
m
m
焦点的位置 焦点在x轴上 焦点在y轴上
范围 __________
____________ __________
____________
顶点 ___________________
___________________ ___________________
___________________
轴长 短轴长=___,长轴长=___
焦点 ___________________ ___________________
焦距 |F1F2|=___
对称性 对称轴_________,对称中心______
离心率 e=_________
-a≤x≤a
且-b≤y≤b
-b≤x≤b
且-a≤y≤a
A1(-a,0)、A2(a,0)
B1(0,-b)、B2(0,b)
A1(0,-a)、A2(0,a)
B1(-b,0)、B2(b,0)
2b
2a
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
2c
x轴和y轴
(0,0)
四、小结:
通径、焦点三角形面积公式
五、作业:
课堂练习:P41 练习:1、2、3、4、
课外作业:P42习题2.1
A组 3、4、5、6、7、8、9
B组 2、3
题型一 由椭圆方程求椭圆的几何性质
例1、求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.
分析: 先将椭圆方程化为标准形式,再利用a、b、c之间的关系求解.
规律方法:解决此类问题的方法是将所给方程先化
为标准形式,然后根据方程判断出椭圆的焦点在哪
个坐标轴上,再利用a,b,c之间的关系和定义,求
椭圆的基本量.
变式1、求椭圆4x2+9y2=36的长轴长和焦距、焦点坐标、顶点坐标和离心率.
分析:解答本题可先
由已知信息判断焦点
所在坐标轴并设出标
准方程,再利用待定
系数法求参数a,b,c.
题型二 由椭圆的几何性质求标准方程
例2、
题型二 由椭圆的几何性质求标准方程
例2、
题型二 由椭圆的几何性质求标准方程
例2、
规律方法:利用性质求椭圆的标准方程,通常
采用待定系数法,而其关键是根据已知条件确
定其标准方程的形式并列出关于参数的关系
式,利用解方程(组)求解,同时注意a、b、
c、e的内在联系以及对方程两种形式的讨论.
变式2、
变式2、
例3、(12分)如图所示,椭圆的中心在原点,焦点F1,F2在x轴上,A,B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,求此椭圆的离心率.
题型三 求椭圆的离心率
∽
(2)在椭圆中涉及三角形问题时,要充分
利用椭圆的定义、正弦定理及余弦定
理、全等三角形、相似三角形等知识.
变式3、
例4、已知在椭圆中,长轴长为2a,焦距为2c,且a+c=10,a-c=4,求椭圆的标准方程.
题型四 分类讨论的思想
分析:由于题目中没有告诉我们焦点的位置,所求标准方程有两种情况:
①焦点在x轴上;
②焦点在y轴上.
规律方法:(1)根据已知条件求椭圆的标准方程的思路是“选标准,定参数”,一般步骤是:①求出a2,b2的值;
②确定焦点所在的坐标轴;③写出标准方程.
(2)当所求椭圆焦点不确定时一定要注意分类讨论.
(3)解此类题要仔细体会方程思想在解题中的应用.
分析:(1)焦点在x轴上;(2)焦点在y轴上.
练习:椭圆离心率的问题
2、求下列适合条件的椭圆的离心率.
(2)若 的左焦点F1到直线AB
(A(-a,0),B(0,b))的距离为 .
练习:
(1)椭圆的一个焦点将长轴分成3:2两段;
3、设椭圆 的两焦点为F1,F2,若在椭圆上存在一点P,使PF1⊥PF2,求椭圆的离心率的取值范围.
练习:椭圆离心率的问题
练习:椭圆离心率的问题
练习:5、已知
的长轴两端点为A,B,如果椭圆上存在一点Q,使∠F1QF2=120°,求离心率e的取值范围.
思考:F1,F2为椭圆的两个焦点,过F2的直线交椭圆于P,Q两点,PF1⊥PQ且|PF1|=|PQ|,求椭圆的离心率.
o
x
y
.
.
P
Q
o
x
y
.
.
P
Q
小结:(椭圆的几何性质)
1、椭圆的范围;
2、椭圆的对称性;
3、椭圆的顶点;
4、椭圆的几何形状;
5、椭圆的第二定义.
M
.
d
o
x
y
.
l
圆锥曲线的第二定义:
M
.
d
圆锥曲线的第二定义:
o
x
y
.
l
焦半径公式
焦点弦
长公式
焦半径:椭圆上的点与焦点两点间距离,称为焦半径.
焦点弦长公式:过焦点的弦叫做焦点弦.
方程:
1
o
F
y
x
2
F
P
y
o
x
图形
小结:
1
o
F
y
x
2
F
P
标准方程
图形
y
o
x
准线方程
焦半径公式
焦点弦
长公式
o
x
y
.
B
A
l
M
2.2.2 椭圆的简单几何性质
第1课时 椭圆的简单几何性质
1、掌握椭圆的简单几何性质;
2、理解离心率对椭圆扁平程度的影响.
重点:椭圆的简单几何性质.
难点:1、求椭圆的离心率;
2、常结合几何图形、方程、不等式、平面向
量等内容命题.
教学目标:
1、椭圆的范围:
2、椭圆的对称性:
3、椭圆的顶点:
4、椭圆的几何形状→扁平程度
变量x,y的取值范围
方程的对称性
x=0或y=0时方程的解
a,b,c
椭圆的性质:
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
椭圆的几何性质:
一、新课引入:
o
x
y
说明:椭圆位于直线 和 所围成的矩形框里.
二、新课讲解:
1、椭圆的范围:
椭圆关于x轴对称;
椭圆关于y轴对称;
椭圆关于原点对称;
故,坐标轴是椭圆的对称轴,原点是椭圆的对称中心.
中心:椭圆的对称中心叫做椭圆的中心.
o
x
y
二、新课讲解:
2、椭圆的对称性:
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点.
长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴.
a、b分别叫做椭圆的长半轴长和短半轴长.
o
x
y
B1(0,-b)
B2(0,b)
A1(-a,0)
A2(a,0)
二、新课讲解:
3、椭圆的顶点:
o
x
y
离心率:椭圆的焦距与长轴长的比,叫做椭圆的离心率.
0
e越接近于0,椭圆越接近于圆.
二、新课讲解:
4、椭圆的离心率:
b→0,e→1,椭圆越扁;
b→a,e→0,椭圆越接近于圆.
二、新课讲解:
4、椭圆的离心率:
用a和b表示椭圆的离心率e
二、新课讲解:
.
.
o
x
y
5、通径:过椭圆的焦点作垂直于长轴的弦叫做通径.
A
B
通径:
半通径:
二、新课讲解:
6、焦点三角形:椭圆上一定与两焦点构成的三角形称为焦点三角形.
所以,焦点三角形面积公式是:
焦点的位置 焦点在x轴上 焦点在y轴上
范围 __________
____________ __________
____________
顶点 ___________________
___________________ ___________________
___________________
轴长 短轴长=___,长轴长=___
焦点 ___________________ ___________________
焦距 |F1F2|=___
对称性 对称轴_________,对称中心______
离心率 e=_________
-a≤x≤a
且-b≤y≤b
-b≤x≤b
且-a≤y≤a
A1(-a,0)、A2(a,0)
B1(0,-b)、B2(0,b)
A1(0,-a)、A2(0,a)
B1(-b,0)、B2(b,0)
2b
2a
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
2c
x轴和y轴
(0,0)
椭圆的性质:
通径、焦点三角形面积公式
1、椭圆几何性质的应用:
(1)椭圆的焦点决定椭圆的位置,范围决定椭圆的大小,离心率决定了椭圆的扁圆程度,对称性是椭圆的重要特征,顶点是椭圆与对称轴的交点,是椭圆重要的特殊点;若已知椭圆的标准方程,则根据a、b的值可确定其性质.
(2)明确a,b的几何意义,a是长半轴长,b是短半轴长,不要与长轴长、短轴长混淆,由c2=a2-b2,可得“已知椭圆的四个顶点,求焦点”的几何作图法,只要以短轴的端点B1(或B2)为圆心,以a为半径作弧交长轴于两点,这两点就是焦点.
点评:
2、椭圆的离心率对椭圆形状的影响:
例4、椭圆16x2+25y2=400的长轴长为____,短轴长为____,焦点坐标为 ,顶点坐标为 , 离心率为
______.
8
10
三、例题分析:
例5、P40
三、例题分析:
M
.
d
o
x
y
.
l
图2.2-12
圆锥曲线的第二定义
三、例题分析:
.
.
o
x
y
图2.2-13
l
m
m
焦点的位置 焦点在x轴上 焦点在y轴上
范围 __________
____________ __________
____________
顶点 ___________________
___________________ ___________________
___________________
轴长 短轴长=___,长轴长=___
焦点 ___________________ ___________________
焦距 |F1F2|=___
对称性 对称轴_________,对称中心______
离心率 e=_________
-a≤x≤a
且-b≤y≤b
-b≤x≤b
且-a≤y≤a
A1(-a,0)、A2(a,0)
B1(0,-b)、B2(0,b)
A1(0,-a)、A2(0,a)
B1(-b,0)、B2(b,0)
2b
2a
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
2c
x轴和y轴
(0,0)
四、小结:
通径、焦点三角形面积公式
五、作业:
课堂练习:P41 练习:1、2、3、4、
课外作业:P42习题2.1
A组 3、4、5、6、7、8、9
B组 2、3
题型一 由椭圆方程求椭圆的几何性质
例1、求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.
分析: 先将椭圆方程化为标准形式,再利用a、b、c之间的关系求解.
规律方法:解决此类问题的方法是将所给方程先化
为标准形式,然后根据方程判断出椭圆的焦点在哪
个坐标轴上,再利用a,b,c之间的关系和定义,求
椭圆的基本量.
变式1、求椭圆4x2+9y2=36的长轴长和焦距、焦点坐标、顶点坐标和离心率.
分析:解答本题可先
由已知信息判断焦点
所在坐标轴并设出标
准方程,再利用待定
系数法求参数a,b,c.
题型二 由椭圆的几何性质求标准方程
例2、
题型二 由椭圆的几何性质求标准方程
例2、
题型二 由椭圆的几何性质求标准方程
例2、
规律方法:利用性质求椭圆的标准方程,通常
采用待定系数法,而其关键是根据已知条件确
定其标准方程的形式并列出关于参数的关系
式,利用解方程(组)求解,同时注意a、b、
c、e的内在联系以及对方程两种形式的讨论.
变式2、
变式2、
例3、(12分)如图所示,椭圆的中心在原点,焦点F1,F2在x轴上,A,B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,求此椭圆的离心率.
题型三 求椭圆的离心率
∽
(2)在椭圆中涉及三角形问题时,要充分
利用椭圆的定义、正弦定理及余弦定
理、全等三角形、相似三角形等知识.
变式3、
例4、已知在椭圆中,长轴长为2a,焦距为2c,且a+c=10,a-c=4,求椭圆的标准方程.
题型四 分类讨论的思想
分析:由于题目中没有告诉我们焦点的位置,所求标准方程有两种情况:
①焦点在x轴上;
②焦点在y轴上.
规律方法:(1)根据已知条件求椭圆的标准方程的思路是“选标准,定参数”,一般步骤是:①求出a2,b2的值;
②确定焦点所在的坐标轴;③写出标准方程.
(2)当所求椭圆焦点不确定时一定要注意分类讨论.
(3)解此类题要仔细体会方程思想在解题中的应用.
分析:(1)焦点在x轴上;(2)焦点在y轴上.
练习:椭圆离心率的问题
2、求下列适合条件的椭圆的离心率.
(2)若 的左焦点F1到直线AB
(A(-a,0),B(0,b))的距离为 .
练习:
(1)椭圆的一个焦点将长轴分成3:2两段;
3、设椭圆 的两焦点为F1,F2,若在椭圆上存在一点P,使PF1⊥PF2,求椭圆的离心率的取值范围.
练习:椭圆离心率的问题
练习:椭圆离心率的问题
练习:5、已知
的长轴两端点为A,B,如果椭圆上存在一点Q,使∠F1QF2=120°,求离心率e的取值范围.
思考:F1,F2为椭圆的两个焦点,过F2的直线交椭圆于P,Q两点,PF1⊥PQ且|PF1|=|PQ|,求椭圆的离心率.
o
x
y
.
.
P
Q
o
x
y
.
.
P
Q
小结:(椭圆的几何性质)
1、椭圆的范围;
2、椭圆的对称性;
3、椭圆的顶点;
4、椭圆的几何形状;
5、椭圆的第二定义.
M
.
d
o
x
y
.
l
圆锥曲线的第二定义:
M
.
d
圆锥曲线的第二定义:
o
x
y
.
l
焦半径公式
焦点弦
长公式
焦半径:椭圆上的点与焦点两点间距离,称为焦半径.
焦点弦长公式:过焦点的弦叫做焦点弦.
方程:
1
o
F
y
x
2
F
P
y
o
x
图形
小结:
1
o
F
y
x
2
F
P
标准方程
图形
y
o
x
准线方程
焦半径公式
焦点弦
长公式
o
x
y
.
B
A
l
M
