高中数学北师大版必修一:4.1 对数与对数运算 课件(17张PPT)
文档属性
| 名称 | 高中数学北师大版必修一:4.1 对数与对数运算 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 347.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 17:18:12 | ||
图片预览





文档简介
4.1 对数与对数的运算
解:设该物质最初的质量是1,则经过x年,该物质的剩留量为
例
题
某种最初质量为1的放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量是原来的84%.写出这种物质的剩留量y关于时间x的函数关系式.
问题情境
问题一
经过了 3 年,剩留量是多少?
数学语言
(已知底数a和指数b,求幂值N)
问题二
经过多少年, 剩留量为 0.5 ?
数学语言
(已知底数a和幂值N ,求指数b)
运算类型
(一种新运算)
指数运算
运算类型
问题情境
,则
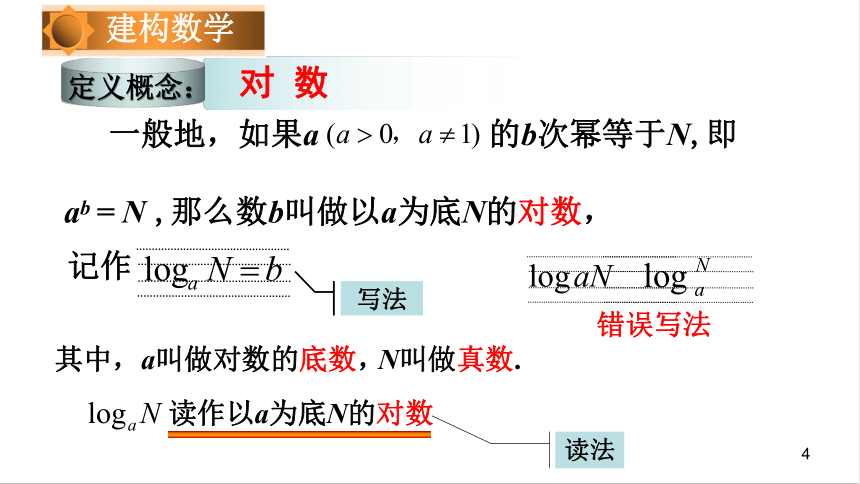
一般地,如果a 的b次幂等于N,即
ab = N ,那么数b叫做以a为底N的对数,
其中,a叫做对数的底数,
N叫做真数.
记作
读法
写法
错误写法
对 数
定义概念:
建构数学
读作以a为底N的对数
通常将以10为底的对数称为常用对数
等.
如
简记作
为了方便起见,对数
等.
如
,
,
常用对数
在科学技术中,常常使用以e为底的对数,
这种对数称为自然对数
是一个无理数.
正数N 的自然对数
简记作
分别记为
如
等.
,
,
,
与自然对数
,
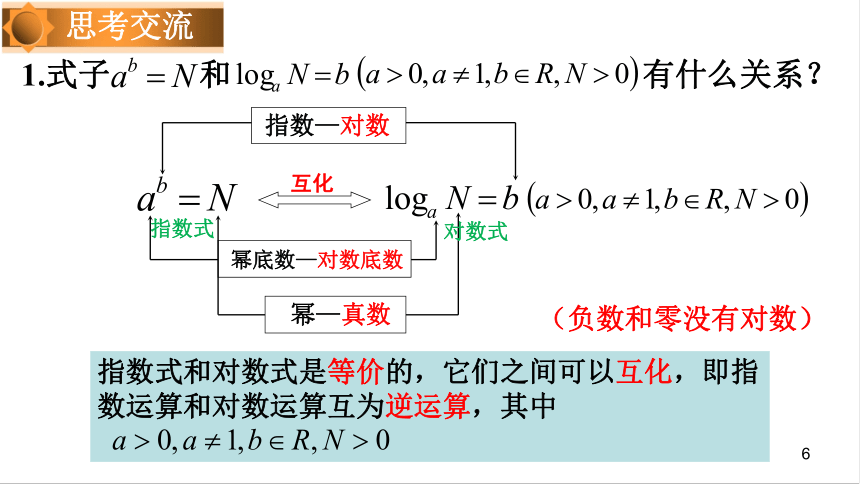
指数式和对数式是等价的,它们之间可以互化,即指数运算和对数运算互为逆运算,其中
1.式子 和 有什么关系?
思考交流
(负数和零没有对数)
互化
指数—对数
幂底数—对数底数
幂—真数
对数式
指数式
对数式
指数式
P79例1:将下列指数式写成对数式:
P80练习1:
问题
经过多少年, 剩留量为 0.5 ?
数学语言
已知底数a和幂值N ,求指数b.
运算类型
对数运算
对数式
指数式
P79例2:将下列对数式写成指数式:
P80练习2:
思考交流
2.对数 , 有什么特点?
互化
根据指数函数图像,它是恒过定点(0,1)的,
所以有 ,它还过一点(1, ),
所以有
根据指数与对数的关系,将其转化为对数式:
得出当 时,对数的两条基本性质为
互化
思考交流
3. 为什么? 为什么?
对数恒等式
当 时,有:
思考交流
4. 零与负数有没有对数? 所有的实数都有对数吗?
∵N>0
∴零与负数没有对数
P79例3:求下列各式的值:
对数基本性质的运用
自主测评例2:求下列各式中的x的值.
自主测评即时训练2-1:求下列各式中的x的值.
课堂总结
1、知道对数式是由指数式转化得到的,即若 ,则 .
会进行指数式与对数式的转化.
2、知道常用对数和自然对数分别是以10为底和以e为底的对数, , 分别简记为 , .
3、知道对数的两个基本性质 , ,及对数恒等式
课后巩固
课本第87页
习题3—4 A组
1(1)(3), 2(2)(4), 3(5)(6)(7)(8)
解:设该物质最初的质量是1,则经过x年,该物质的剩留量为
例
题
某种最初质量为1的放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量是原来的84%.写出这种物质的剩留量y关于时间x的函数关系式.
问题情境
问题一
经过了 3 年,剩留量是多少?
数学语言
(已知底数a和指数b,求幂值N)
问题二
经过多少年, 剩留量为 0.5 ?
数学语言
(已知底数a和幂值N ,求指数b)
运算类型
(一种新运算)
指数运算
运算类型
问题情境
,则
一般地,如果a 的b次幂等于N,即
ab = N ,那么数b叫做以a为底N的对数,
其中,a叫做对数的底数,
N叫做真数.
记作
读法
写法
错误写法
对 数
定义概念:
建构数学
读作以a为底N的对数
通常将以10为底的对数称为常用对数
等.
如
简记作
为了方便起见,对数
等.
如
,
,
常用对数
在科学技术中,常常使用以e为底的对数,
这种对数称为自然对数
是一个无理数.
正数N 的自然对数
简记作
分别记为
如
等.
,
,
,
与自然对数
,
指数式和对数式是等价的,它们之间可以互化,即指数运算和对数运算互为逆运算,其中
1.式子 和 有什么关系?
思考交流
(负数和零没有对数)
互化
指数—对数
幂底数—对数底数
幂—真数
对数式
指数式
对数式
指数式
P79例1:将下列指数式写成对数式:
P80练习1:
问题
经过多少年, 剩留量为 0.5 ?
数学语言
已知底数a和幂值N ,求指数b.
运算类型
对数运算
对数式
指数式
P79例2:将下列对数式写成指数式:
P80练习2:
思考交流
2.对数 , 有什么特点?
互化
根据指数函数图像,它是恒过定点(0,1)的,
所以有 ,它还过一点(1, ),
所以有
根据指数与对数的关系,将其转化为对数式:
得出当 时,对数的两条基本性质为
互化
思考交流
3. 为什么? 为什么?
对数恒等式
当 时,有:
思考交流
4. 零与负数有没有对数? 所有的实数都有对数吗?
∵N>0
∴零与负数没有对数
P79例3:求下列各式的值:
对数基本性质的运用
自主测评例2:求下列各式中的x的值.
自主测评即时训练2-1:求下列各式中的x的值.
课堂总结
1、知道对数式是由指数式转化得到的,即若 ,则 .
会进行指数式与对数式的转化.
2、知道常用对数和自然对数分别是以10为底和以e为底的对数, , 分别简记为 , .
3、知道对数的两个基本性质 , ,及对数恒等式
课后巩固
课本第87页
习题3—4 A组
1(1)(3), 2(2)(4), 3(5)(6)(7)(8)
