高中数学人教A版必修1第一章1.3.1 函数的单调性课件(12张PPT)
文档属性
| 名称 | 高中数学人教A版必修1第一章1.3.1 函数的单调性课件(12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 871.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 17:24:10 | ||
图片预览



文档简介
☆
★
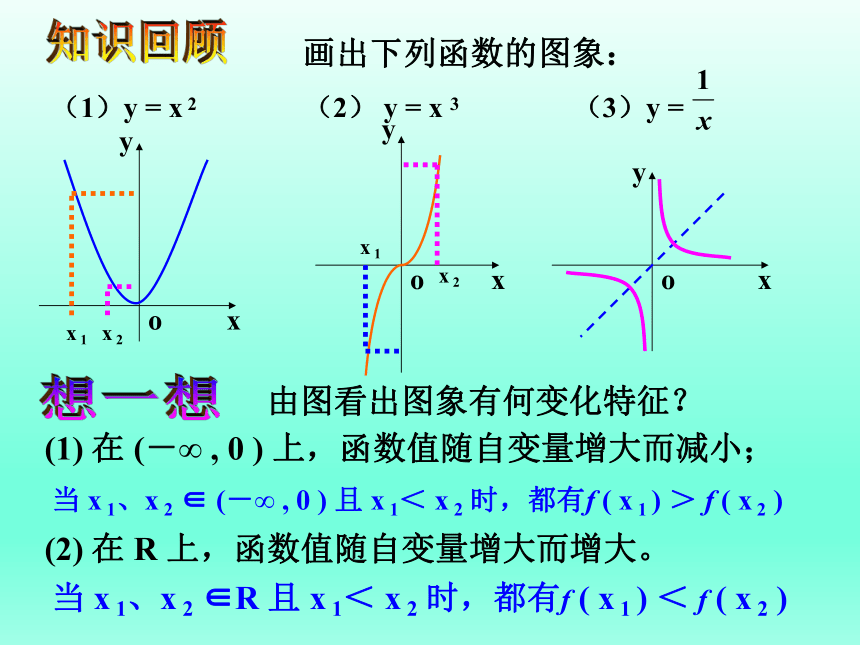
画出下列函数的图象:
(1)y = x 2 (2) y = x 3 (3)y =
y
x
o
y
x
o
y
x
o
由图看出图象有何变化特征?
x 2
x 1
x 1
x 2
(1) 在 (-∞ , 0 ) 上,函数值随自变量增大而减小;
(2) 在 R 上,函数值随自变量增大而增大。
当 x 1、x 2 ∈ (-∞ , 0 ) 且 x 1< x 2 时,都有f ( x 1 ) > f ( x 2 )
当 x 1、x 2 ∈R 且 x 1< x 2 时,都有f ( x 1 ) < f ( x 2 )
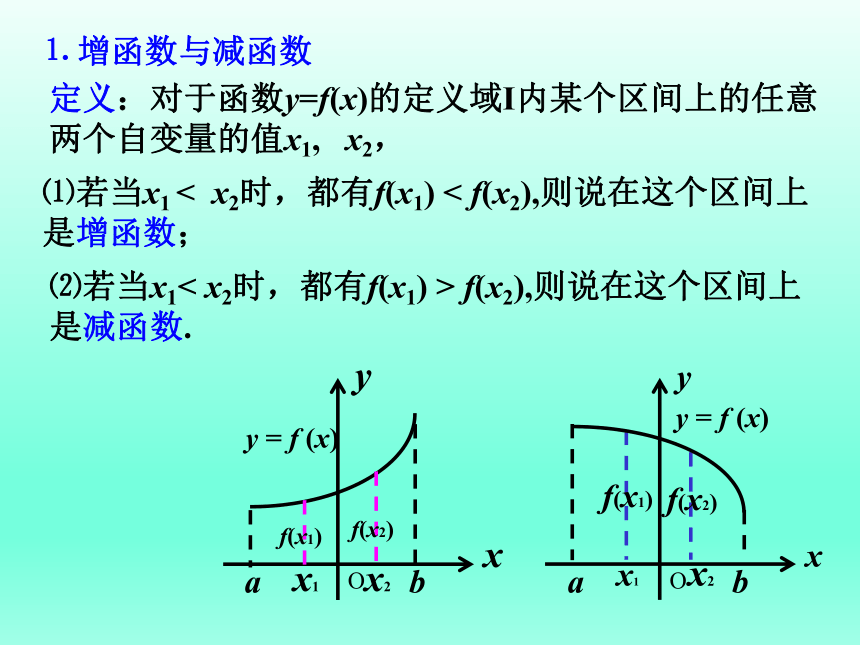
⒈ 增函数与减函数
定义:对于函数y=f(x)的定义域I内某个区间上的任意两个自变量的值x1, x2,
⑴若当x1 < x2时,都有f(x1) < f(x2),则说在这个区间上是增函数;
⑵若当x1< x2时,都有f(x1) > f(x2),则说在这个区间上是减函数.
a
b
O
x
y
y = f (x)
x2
x1
f(x1)
f(x2)
y = f (x)
x2
x1
f(x1)
f(x2)
O
x
y
a
b
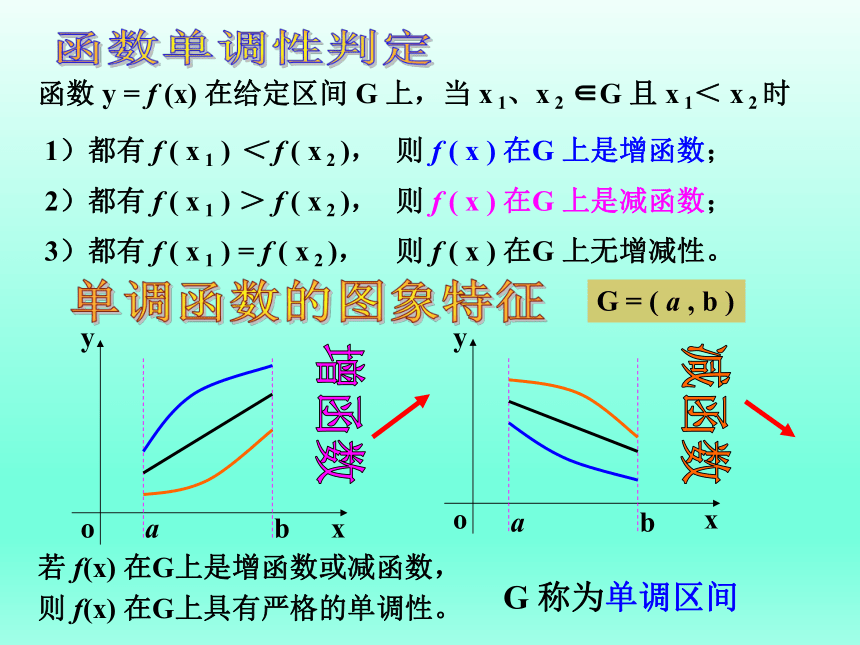
函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时
y
x
o
a
b
y
x
o
a
b
1)都有 f ( x 1 ) < f ( x 2 ),
则 f ( x ) 在G 上是增函数;
2)都有 f ( x 1 ) > f ( x 2 ),
则 f ( x ) 在G 上是减函数;
3)都有 f ( x 1 ) = f ( x 2 ),
则 f ( x ) 在G 上无增减性。
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上具有严格的单调性。
G 称为单调区间
G = ( a , b )
(1)函数的单调性也叫函数的增减性;
(2)函数的单调性是对某个区间而言的,
它是个局部概念。这个区间是定义域的子集。
(3)单调区间:针对自变量 x 而言的。
若函数在此区间上是增函数,则为单调递增
区间;若函数在此区间上是减函数,则为单
调递减区间
1、证明:函数 f ( x ) = - + 1 在 ( 0 , + ∞ )
上是增函数。
证:设 0 < x 1 < x 2 < + ∞
则 f ( x 1 ) -f ( x 2 )
∵ 0 < x 1 < x 2 < + ∞
∴ x 1 -x 2 < 0
即 f ( x 1 ) -f ( x 2 ) < 0
∴ f ( x 1 ) < f ( x 2 )
故 此函数在 ( 0 , + ∞ ) 上是增函数。
①
②
③
2、判断函数 f ( x ) = 在区间 (-1 , 1 ) 上的单调性。
解:设 -1 < x 1 < x 2 < 1
则 f ( x 1 ) -f ( x 2 )
∵ -1 < x 1 < x 2 < 1
∴ 1 + x 1x 2 > 0,x 2 -x 1 >0
∴ f ( x 2 ) -f ( x 1 ) >0
即 f ( x 2 ) > f ( x 1 )
故此函数在 (-1 , 1 ) 上是增函数
3、求函数 y = 2x 2 -4x + 1 的单调区间
4、写出图中函数的单调区间
x
y
o
1
-5
4
解:由题 y = 2( x -1 ) 2 -1
y
x
o
1
1
-1
由图知:单调递增区间为 [ 1 , + ∞)
单调递减区间为 (- ∞ , 1 ]
解:由图知:
单调递增区间为
[-5 , 1 ] ,[ 4 , + ∞)
单调递减区间为
(- ∞ , -5 ],[ 1 , 4 ]
单调区间之间用逗号分开
1、单调性是针对某个区间而言的,是个局部概念。
2、单调性的证明步骤:
1)取量定大小;
2)作差定符号;
3)判断定结论。
3、单调区间的求法:
1)通常用图象直接写出;
2)利用单调性证明后得出。
设 x 1、x 2 ∈给定区间, 且 x 1< x 2
f(x 1)-f(x 2)的结果化积或化完全平方
式的和;
判断f(x 1) 与 f(x 2) 的大小 ,下结论,
结论一定要指出在那个区间上。
针对 x 而言的
1. 判断函数 f (x) = x2+1在
(0, +∞)上是增函数还是减函数?
2. 若函数f (x) 在区间[a, b]及
(b, c]上都单调递减, 则f (x)在区间
[a, c]上的单调性为 ( )
A. 单调递减;
B. 单调递增;
C. 一定不单调;
D. 不确定.
D
练习实践
3. 函数f (x)=
2x+1, (x≥1)
5 - x, (x<1)
则f (x)的递减区间为( )
A. [1, +∞)
B. (-∞, 1)
C. (0, +∞)
D. (-∞, 1]
B
4. 若函数f (x) 在区间[a, b]单调
且 f(a) f(b)<0, 则方程f(x)=0在区
.
间[a, b]上( ).
A.至少有一实根;
B.至多有一实根;
C.没有一实根;
D.必有唯一实根.
D
★
画出下列函数的图象:
(1)y = x 2 (2) y = x 3 (3)y =
y
x
o
y
x
o
y
x
o
由图看出图象有何变化特征?
x 2
x 1
x 1
x 2
(1) 在 (-∞ , 0 ) 上,函数值随自变量增大而减小;
(2) 在 R 上,函数值随自变量增大而增大。
当 x 1、x 2 ∈ (-∞ , 0 ) 且 x 1< x 2 时,都有f ( x 1 ) > f ( x 2 )
当 x 1、x 2 ∈R 且 x 1< x 2 时,都有f ( x 1 ) < f ( x 2 )
⒈ 增函数与减函数
定义:对于函数y=f(x)的定义域I内某个区间上的任意两个自变量的值x1, x2,
⑴若当x1 < x2时,都有f(x1) < f(x2),则说在这个区间上是增函数;
⑵若当x1< x2时,都有f(x1) > f(x2),则说在这个区间上是减函数.
a
b
O
x
y
y = f (x)
x2
x1
f(x1)
f(x2)
y = f (x)
x2
x1
f(x1)
f(x2)
O
x
y
a
b
函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时
y
x
o
a
b
y
x
o
a
b
1)都有 f ( x 1 ) < f ( x 2 ),
则 f ( x ) 在G 上是增函数;
2)都有 f ( x 1 ) > f ( x 2 ),
则 f ( x ) 在G 上是减函数;
3)都有 f ( x 1 ) = f ( x 2 ),
则 f ( x ) 在G 上无增减性。
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上具有严格的单调性。
G 称为单调区间
G = ( a , b )
(1)函数的单调性也叫函数的增减性;
(2)函数的单调性是对某个区间而言的,
它是个局部概念。这个区间是定义域的子集。
(3)单调区间:针对自变量 x 而言的。
若函数在此区间上是增函数,则为单调递增
区间;若函数在此区间上是减函数,则为单
调递减区间
1、证明:函数 f ( x ) = - + 1 在 ( 0 , + ∞ )
上是增函数。
证:设 0 < x 1 < x 2 < + ∞
则 f ( x 1 ) -f ( x 2 )
∵ 0 < x 1 < x 2 < + ∞
∴ x 1 -x 2 < 0
即 f ( x 1 ) -f ( x 2 ) < 0
∴ f ( x 1 ) < f ( x 2 )
故 此函数在 ( 0 , + ∞ ) 上是增函数。
①
②
③
2、判断函数 f ( x ) = 在区间 (-1 , 1 ) 上的单调性。
解:设 -1 < x 1 < x 2 < 1
则 f ( x 1 ) -f ( x 2 )
∵ -1 < x 1 < x 2 < 1
∴ 1 + x 1x 2 > 0,x 2 -x 1 >0
∴ f ( x 2 ) -f ( x 1 ) >0
即 f ( x 2 ) > f ( x 1 )
故此函数在 (-1 , 1 ) 上是增函数
3、求函数 y = 2x 2 -4x + 1 的单调区间
4、写出图中函数的单调区间
x
y
o
1
-5
4
解:由题 y = 2( x -1 ) 2 -1
y
x
o
1
1
-1
由图知:单调递增区间为 [ 1 , + ∞)
单调递减区间为 (- ∞ , 1 ]
解:由图知:
单调递增区间为
[-5 , 1 ] ,[ 4 , + ∞)
单调递减区间为
(- ∞ , -5 ],[ 1 , 4 ]
单调区间之间用逗号分开
1、单调性是针对某个区间而言的,是个局部概念。
2、单调性的证明步骤:
1)取量定大小;
2)作差定符号;
3)判断定结论。
3、单调区间的求法:
1)通常用图象直接写出;
2)利用单调性证明后得出。
设 x 1、x 2 ∈给定区间, 且 x 1< x 2
f(x 1)-f(x 2)的结果化积或化完全平方
式的和;
判断f(x 1) 与 f(x 2) 的大小 ,下结论,
结论一定要指出在那个区间上。
针对 x 而言的
1. 判断函数 f (x) = x2+1在
(0, +∞)上是增函数还是减函数?
2. 若函数f (x) 在区间[a, b]及
(b, c]上都单调递减, 则f (x)在区间
[a, c]上的单调性为 ( )
A. 单调递减;
B. 单调递增;
C. 一定不单调;
D. 不确定.
D
练习实践
3. 函数f (x)=
2x+1, (x≥1)
5 - x, (x<1)
则f (x)的递减区间为( )
A. [1, +∞)
B. (-∞, 1)
C. (0, +∞)
D. (-∞, 1]
B
4. 若函数f (x) 在区间[a, b]单调
且 f(a) f(b)<0, 则方程f(x)=0在区
.
间[a, b]上( ).
A.至少有一实根;
B.至多有一实根;
C.没有一实根;
D.必有唯一实根.
D
