高中数学人教A版必修2第二章 2.2.3 直线与平面平行的性质 课件(18张PPT)
文档属性
| 名称 | 高中数学人教A版必修2第二章 2.2.3 直线与平面平行的性质 课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 847.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 17:30:50 | ||
图片预览


文档简介
2.2.3 直线与平面平行的性质
a
b
α
a
α
b
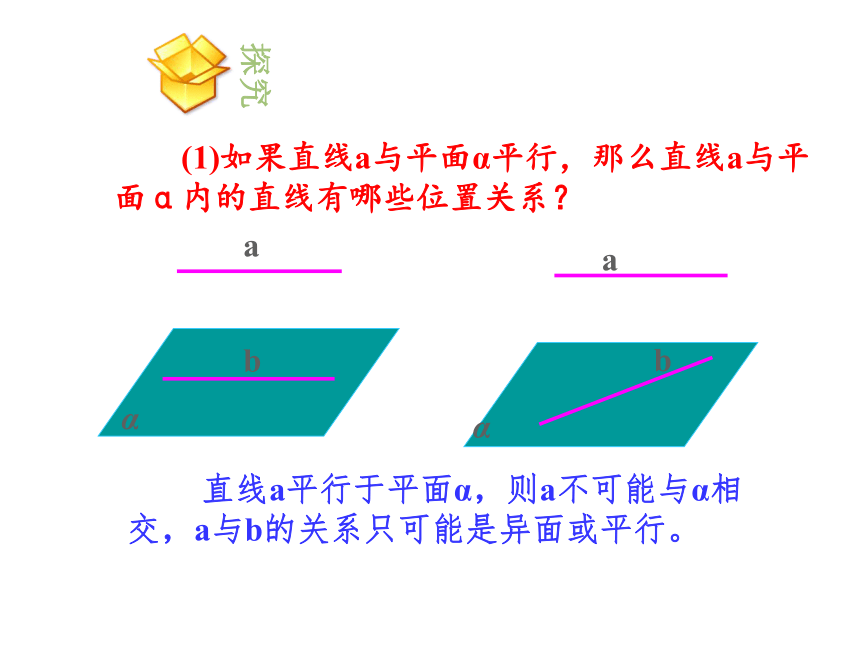
直线a平行于平面α,则a不可能与α相交,a与b的关系只可能是异面或平行。
探究
(1)如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?
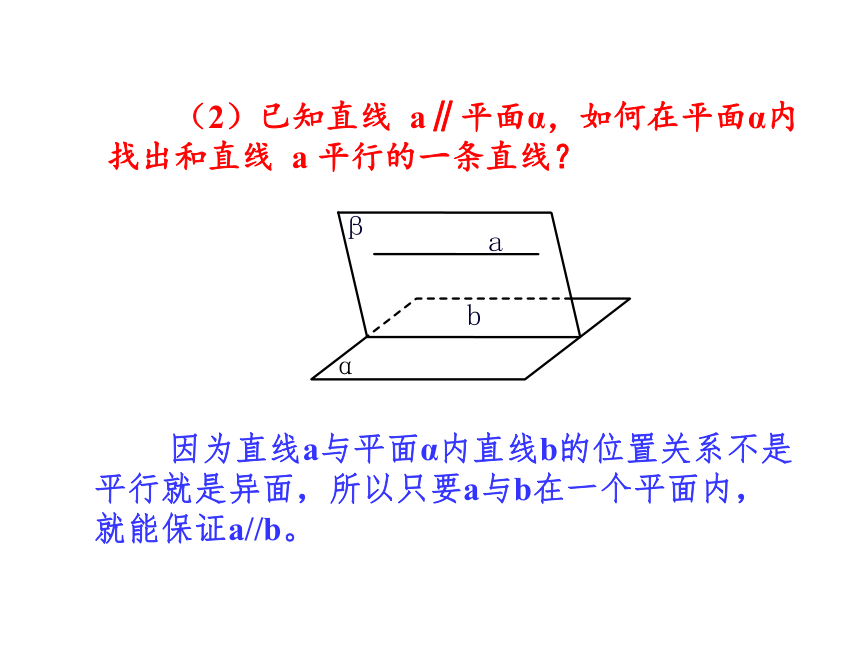
(2)已知直线 a∥平面α,如何在平面α内找出和直线 a 平行的一条直线?
因为直线a与平面α内直线b的位置关系不是平行就是异面,所以只要a与b在一个平面内,就能保证a//b。
直线和平面平行的性质定理:
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
符号表示:
面面相交、线面平行 线线平行
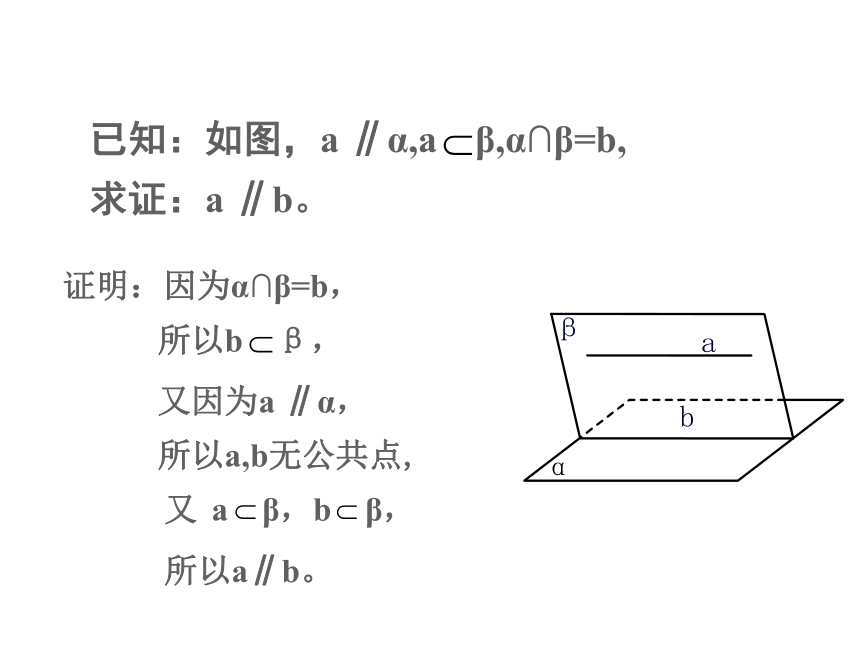
证明:因为α∩β=b,
所以a,b无公共点,
已知:如图,a ∥α,a β,α∩β=b,
求证:a ∥b。
所以b β,
a β,b β,
又
又因为a ∥α,
所以a∥b。
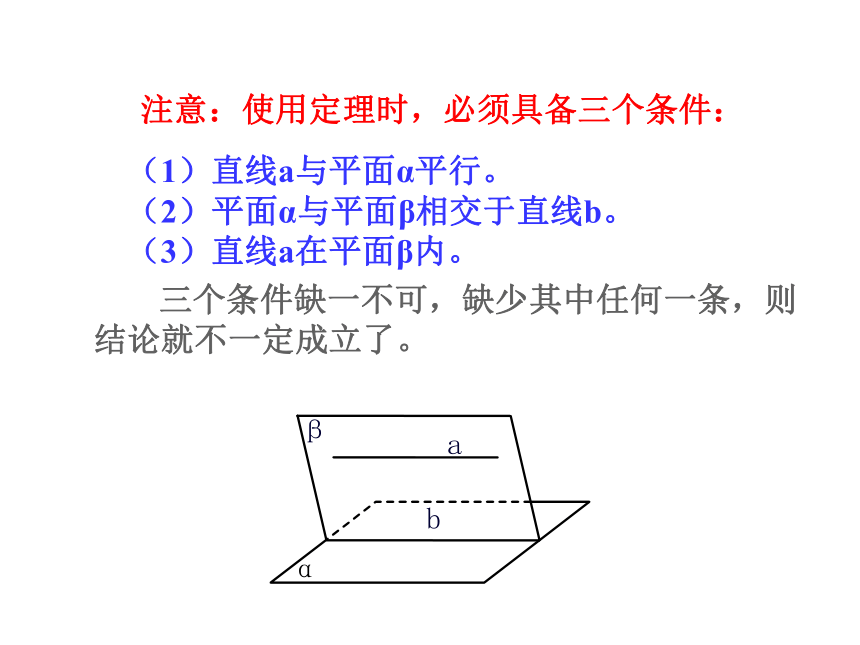
注意:使用定理时,必须具备三个条件:
(1)直线a与平面α平行。
(2)平面α与平面β相交于直线b。
(3)直线a在平面β内。
三个条件缺一不可,缺少其中任何一条,则结论就不一定成立了。
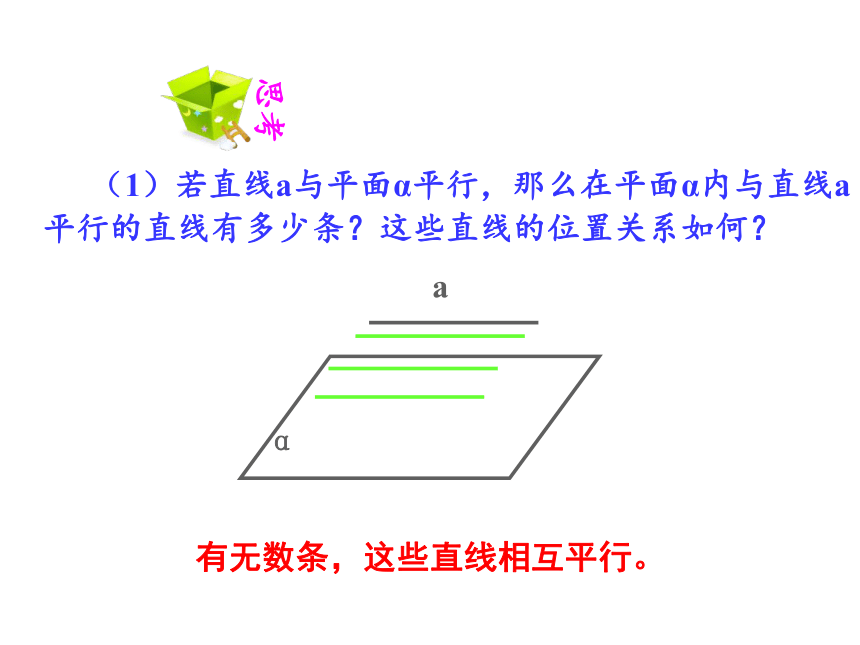
(1)若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?
a
α
思考
有无数条,这些直线相互平行。
(2)如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?
α
a
α
a
(3)如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?
α
a
b
如图所示的一块木料中,棱BC//平面A'C',
(1)要经过面A'C'内的一点P和棱BC将木料锯开,应该怎样画线?
(2)所画的线和平面AC是什么位置关系?
例五
A
A′
C
B
D
P
D′
B′
C′
解:(1)在平面A'C'内,过点P作直线EF,使EF ∥ B'C',并分别交棱A'B',C'D'于点E,F。连BE,CF.则EF,BE,CF就是应画的线。
A
A′
C
B
D
P
D′
B′
C′
E
F
(2)因为棱BC平行于平面A'C',平面BC'与平面A'C'交于B'C',所以,BC ∥ B'C'.由1知,EF ∥ B'C' ,所以EF ∥ BC,因此EF ∥ BC,EF不在平面AC,BC在平面AC上,从而EF ∥平面AC. BE,CF显然都与面AC相交。
A
A′
C
B
D
P
D′
B′
C′
E
F
例六
l
α
β
求证:如果两个相交平面分别经过两条平行直线中的一条,那么它们的交线和这两条直线平行。
a
b
已知:直线a//直线b,平面α交平面β于直线l。
求证:a//l, b//l。
证明:
因为a//b,
根据直线与平面平行的判定定理,
直线a//面β,
又根据直线与平面平行的性质定理,
直线a//直线l,
同理,直线b//直线l。
课堂小结
线线平行 线面平行
线面平行 线线平行
线面平行的判定定理
线面平行的性质定理
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
直线与平面之间的位置关系同直线与直线之间的位置关系的相互转化是立体几何的一种重要思想。
在解决问题时注意转化思想的应用如在例题四中
线线平行
线面平行
转化为
转化为
线线平行
随堂练习
1.如果一条直线和一个平面平行,则这条直线( )
A. 只和这个平面内一条直线平行
B. 只和这个平面内两条相交直线不相交
C. 和这个平面内的任意直线都平行
D. 和这个平面内的任意直线都不相交
D
2.直线a ∥平面α,平面α内有n条互相平行的直线,那么这n条直线和直线a( )
A. 全平行
B. 全异面
C. 全平行或全异面
D. 不全平行或不全异面
B
3.直线a∥平面α,平面α内有n条交于一点的直线,那么这n条直线和直线a 平行的 ( )
A.至少有一条 B.至多有一条
C.有且只有一条 D.不可能有
C
4.已知平面外的两条平行直线中的一条平行于这个平面,求证另一条也平行于这个平面。
c
a
b
α
如图,已知直线a,b和平面α ,a∥b,a∥α , a,b都在平面α外 。
求证:b∥α
a
b
α
a
α
b
直线a平行于平面α,则a不可能与α相交,a与b的关系只可能是异面或平行。
探究
(1)如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?
(2)已知直线 a∥平面α,如何在平面α内找出和直线 a 平行的一条直线?
因为直线a与平面α内直线b的位置关系不是平行就是异面,所以只要a与b在一个平面内,就能保证a//b。
直线和平面平行的性质定理:
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
符号表示:
面面相交、线面平行 线线平行
证明:因为α∩β=b,
所以a,b无公共点,
已知:如图,a ∥α,a β,α∩β=b,
求证:a ∥b。
所以b β,
a β,b β,
又
又因为a ∥α,
所以a∥b。
注意:使用定理时,必须具备三个条件:
(1)直线a与平面α平行。
(2)平面α与平面β相交于直线b。
(3)直线a在平面β内。
三个条件缺一不可,缺少其中任何一条,则结论就不一定成立了。
(1)若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?
a
α
思考
有无数条,这些直线相互平行。
(2)如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?
α
a
α
a
(3)如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?
α
a
b
如图所示的一块木料中,棱BC//平面A'C',
(1)要经过面A'C'内的一点P和棱BC将木料锯开,应该怎样画线?
(2)所画的线和平面AC是什么位置关系?
例五
A
A′
C
B
D
P
D′
B′
C′
解:(1)在平面A'C'内,过点P作直线EF,使EF ∥ B'C',并分别交棱A'B',C'D'于点E,F。连BE,CF.则EF,BE,CF就是应画的线。
A
A′
C
B
D
P
D′
B′
C′
E
F
(2)因为棱BC平行于平面A'C',平面BC'与平面A'C'交于B'C',所以,BC ∥ B'C'.由1知,EF ∥ B'C' ,所以EF ∥ BC,因此EF ∥ BC,EF不在平面AC,BC在平面AC上,从而EF ∥平面AC. BE,CF显然都与面AC相交。
A
A′
C
B
D
P
D′
B′
C′
E
F
例六
l
α
β
求证:如果两个相交平面分别经过两条平行直线中的一条,那么它们的交线和这两条直线平行。
a
b
已知:直线a//直线b,平面α交平面β于直线l。
求证:a//l, b//l。
证明:
因为a//b,
根据直线与平面平行的判定定理,
直线a//面β,
又根据直线与平面平行的性质定理,
直线a//直线l,
同理,直线b//直线l。
课堂小结
线线平行 线面平行
线面平行 线线平行
线面平行的判定定理
线面平行的性质定理
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
直线与平面之间的位置关系同直线与直线之间的位置关系的相互转化是立体几何的一种重要思想。
在解决问题时注意转化思想的应用如在例题四中
线线平行
线面平行
转化为
转化为
线线平行
随堂练习
1.如果一条直线和一个平面平行,则这条直线( )
A. 只和这个平面内一条直线平行
B. 只和这个平面内两条相交直线不相交
C. 和这个平面内的任意直线都平行
D. 和这个平面内的任意直线都不相交
D
2.直线a ∥平面α,平面α内有n条互相平行的直线,那么这n条直线和直线a( )
A. 全平行
B. 全异面
C. 全平行或全异面
D. 不全平行或不全异面
B
3.直线a∥平面α,平面α内有n条交于一点的直线,那么这n条直线和直线a 平行的 ( )
A.至少有一条 B.至多有一条
C.有且只有一条 D.不可能有
C
4.已知平面外的两条平行直线中的一条平行于这个平面,求证另一条也平行于这个平面。
c
a
b
α
如图,已知直线a,b和平面α ,a∥b,a∥α , a,b都在平面α外 。
求证:b∥α
