高中数学人教A版必修5第一章1.1.1 正弦定理 课件(19张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第一章1.1.1 正弦定理 课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 686.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 17:31:04 | ||
图片预览




文档简介
第一章 解三角形
1 导入
近测高塔远看山,量天度海只等闲。
古有九章勾股法,今看三角正余弦。
边角角边细推算,周长面积巧周旋。
小小三角奥妙多,品味佳酿越千年。
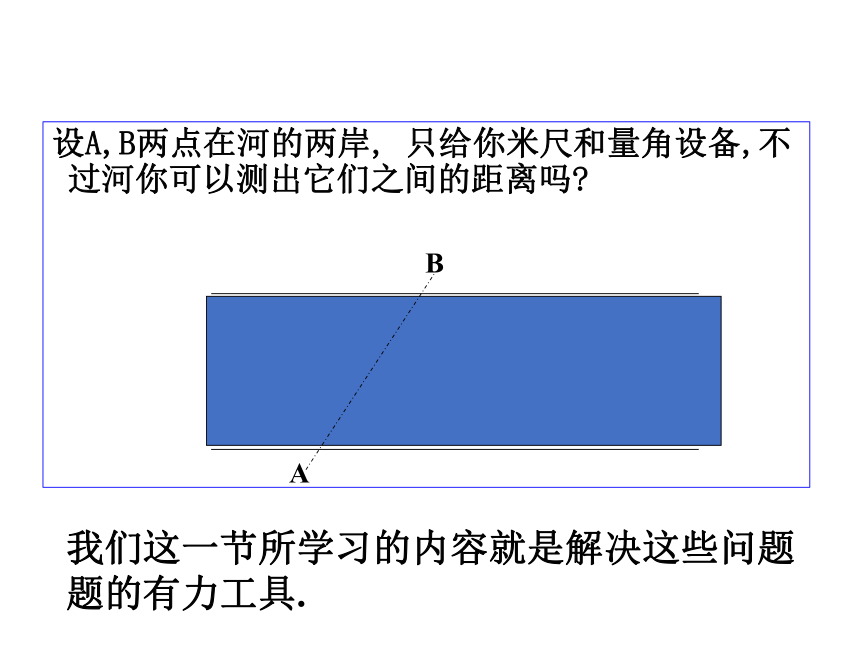
设A,B两点在河的两岸, 只给你米尺和量角设备,不过河你可以测出它们之间的距离吗?
A
B
我们这一节所学习的内容就是解决这些问题
题的有力工具.
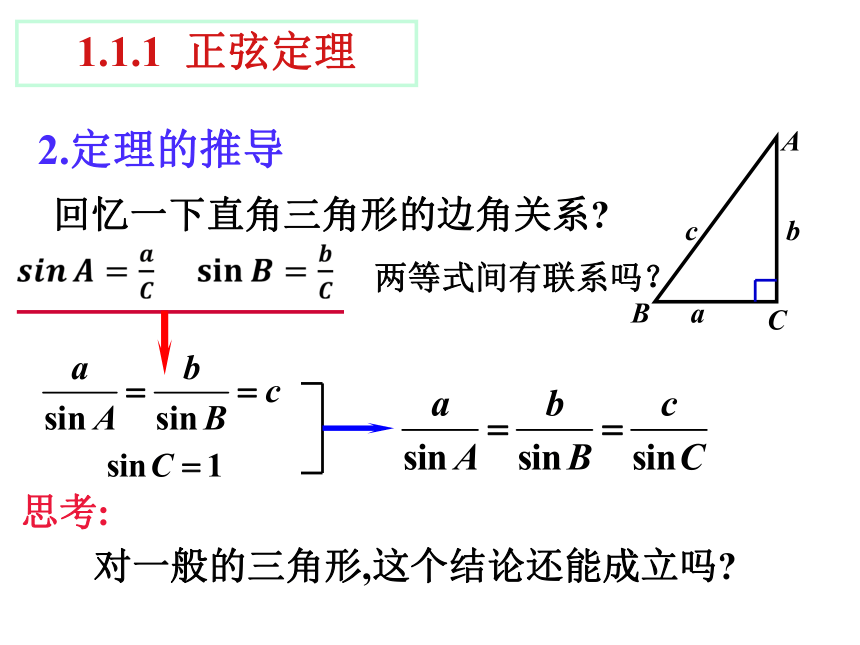
回忆一下直角三角形的边角关系?
A
B
C
c
b
a
两等式间有联系吗?
思考:
对一般的三角形,这个结论还能成立吗?
2.定理的推导
1.1.1 正弦定理
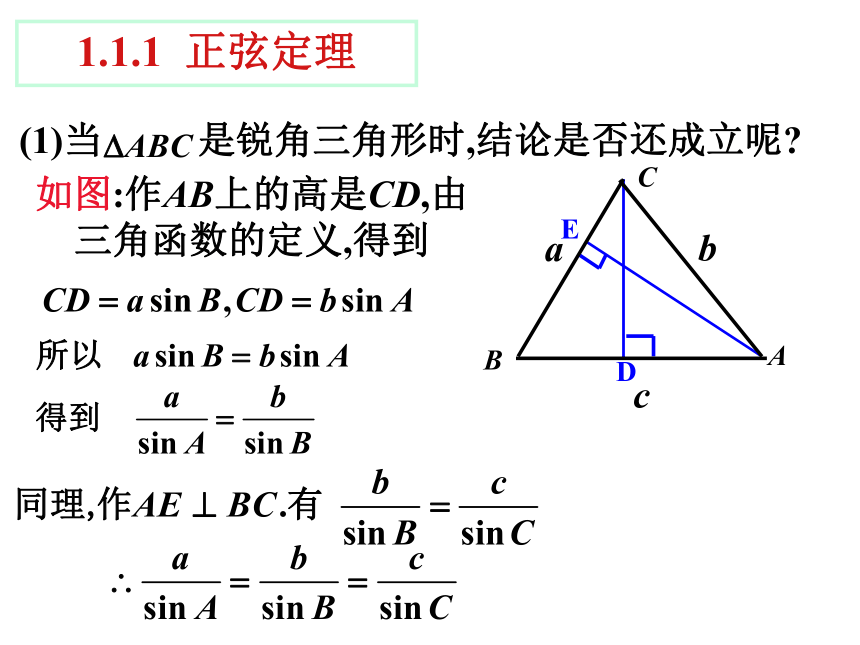
(1)当 是锐角三角形时,结论是否还成立呢?
D
如图:作AB上的高是CD,由
三角函数的定义,得到
1.1.1 正弦定理
B
A
C
a
b
c
E
(2)当 是钝角三角形时,以上等式是否仍然成立?
B
A
C
b
c
a
D
正弦定理 在一个三角形中,各边和它所 对角的正弦的比相等,即
含三角形的三边及三内角
定理结构特征:
1.1.1 正弦定理
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫解三角形
剖析定理、加深理解
可以解决三角形中两类的问题:
①
已知两角和一边,求其他角和边
②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角
例1 在 中, 已知 ,
解三角形.
已知两个内角和任何一边,解三角形
3.定理的应用举例
(1)
已知 , 求
练习一
(2)已知 ,求
在△ABC中
例2、
已知a=16, b= , A=30°,解三角形
已知两边和其中一边的对角,解三角形
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
C=90°
C=30°
当B=120°时
B
16
300
A
B
C
16
3
16
8
3
练习二
B=300
无解
4.探究课题引入时问题(2)的解决方法
A
B
C
b
c
1.1.1 正弦定理
(2R为△ABC外接圆直径)
例3
证明:????当三角形ABC为锐角三角形时,做外接圆O,过B作直径BC,连AC
O
C/
c
b
a
C
B
A
.
D
O
C
A
B
a
由公式得:
公式变形:
③
①
②
作用:可实现边角之间的互化,
(3)在 中,若 ,
则 是( )
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等边三角形
(1)在 中,
D
练习
一个定理
两个应用
一个思想:
(1) 已知两角及任意一边,可以求出其他两边和另一角;
(2)已知两边和其中一边的对角,可以求出三角形的其他的边和角。(此时可能有一解、二解、无解)
1.1.1 正弦定理
小结:
有特殊到一般的探究问题的思想.
1 导入
近测高塔远看山,量天度海只等闲。
古有九章勾股法,今看三角正余弦。
边角角边细推算,周长面积巧周旋。
小小三角奥妙多,品味佳酿越千年。
设A,B两点在河的两岸, 只给你米尺和量角设备,不过河你可以测出它们之间的距离吗?
A
B
我们这一节所学习的内容就是解决这些问题
题的有力工具.
回忆一下直角三角形的边角关系?
A
B
C
c
b
a
两等式间有联系吗?
思考:
对一般的三角形,这个结论还能成立吗?
2.定理的推导
1.1.1 正弦定理
(1)当 是锐角三角形时,结论是否还成立呢?
D
如图:作AB上的高是CD,由
三角函数的定义,得到
1.1.1 正弦定理
B
A
C
a
b
c
E
(2)当 是钝角三角形时,以上等式是否仍然成立?
B
A
C
b
c
a
D
正弦定理 在一个三角形中,各边和它所 对角的正弦的比相等,即
含三角形的三边及三内角
定理结构特征:
1.1.1 正弦定理
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫解三角形
剖析定理、加深理解
可以解决三角形中两类的问题:
①
已知两角和一边,求其他角和边
②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角
例1 在 中, 已知 ,
解三角形.
已知两个内角和任何一边,解三角形
3.定理的应用举例
(1)
已知 , 求
练习一
(2)已知 ,求
在△ABC中
例2、
已知a=16, b= , A=30°,解三角形
已知两边和其中一边的对角,解三角形
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
C=90°
C=30°
当B=120°时
B
16
300
A
B
C
16
3
16
8
3
练习二
B=300
无解
4.探究课题引入时问题(2)的解决方法
A
B
C
b
c
1.1.1 正弦定理
(2R为△ABC外接圆直径)
例3
证明:????当三角形ABC为锐角三角形时,做外接圆O,过B作直径BC,连AC
O
C/
c
b
a
C
B
A
.
D
O
C
A
B
a
由公式得:
公式变形:
③
①
②
作用:可实现边角之间的互化,
(3)在 中,若 ,
则 是( )
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等边三角形
(1)在 中,
D
练习
一个定理
两个应用
一个思想:
(1) 已知两角及任意一边,可以求出其他两边和另一角;
(2)已知两边和其中一边的对角,可以求出三角形的其他的边和角。(此时可能有一解、二解、无解)
1.1.1 正弦定理
小结:
有特殊到一般的探究问题的思想.
