高中数学人教A版必修二2.3.3直线与平面垂直的性质课件(14张PPT)
文档属性
| 名称 | 高中数学人教A版必修二2.3.3直线与平面垂直的性质课件(14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 184.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览





文档简介
直线与平面垂直的性质
1、线面垂直的概念
2、如何判定线面垂直?
1、定义
2、判定定理
3、例1的结论
3、在空间,过一点,有几条直线与已知平面垂直?过一点,有几个平面与已知直线垂直?
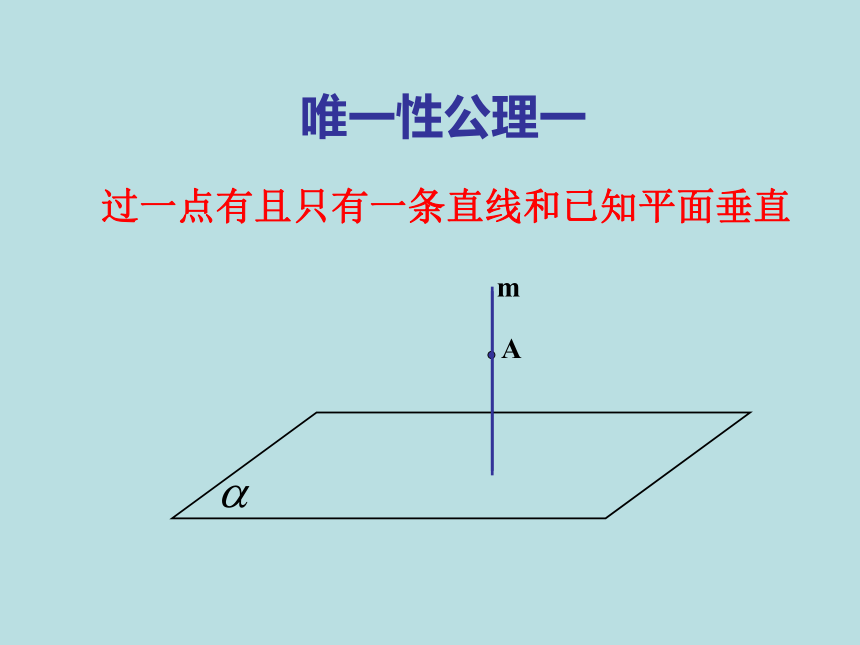
唯一性公理一
m
A
过一点有且只有一条直线和已知平面垂直
唯一性公理二
过一点有且只有一个平面和已知直线垂直
m
A
B
如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面.
4、我们已经知道:
那么:
如果两条直线同垂直于一个平面,那么这两条直线是否平行?
直线与平面垂直的性质定理:
如果两条直线同垂直于一个平面,
那么这两条直线平行.
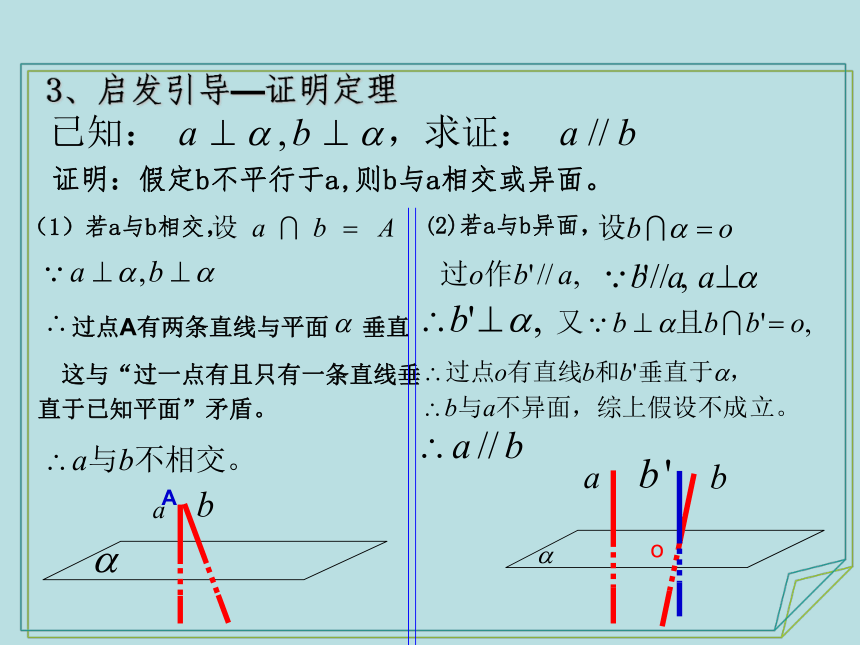
3、启发引导—证明定理
A
(1)若a与b相交,
证明:假定b不平行于a,则b与a相交或异面。
过点A有两条直线与平面 垂直
这与“过一点有且只有一条直线垂
直于已知平面”矛盾。
o
(2)若a与b异面,
4、自主探究—深化定理
问题③:
如果两条直线与平面所成的角相等,则两直线平行吗?
结论:平行、相交、异面
a
b
1
2
o1
o2
a
b
A1
A2
1
2
o1
o2
a
1
2
b
o1
o2
a
b
√
×
1、判断下列命题的正误。
(2)垂直于同一直线的两条直线互相平行( )
(3)平行于同一平面的两条直线互相平行( )
(4)垂直于同一平面的两条直线互相平行( )
×
(1)平行于同一直线的两条直线互相平行( )
√
五、过程设计
(三) 线面垂直性质定理的应用
小牛试刀
例1 已知:平面 =AB,PC ,PD ,垂足分
别是C、D,求证: AB CD 。
P
A
B
C
D
H
理论迁移
如图,已知 于点A, 于点B,
求证: .
A
B
C
α
β
l
a
(2)若 ,求证:MN 面PCD
例2 如图,已知 矩形ABCD所在平面,M、N分别是AB、PC的中点求证: (1)
P
A
B
C
D
M
N
E
A
D
C
B
A1
B1
C1
D1
练习:如图,在正方体ABCD-A1B1C1D1中,EF是异面直线AC与A1D的公垂线,求证:EF//BD1.
E
F
提示:异面直线的公垂线是指和两条异面直线都垂直相交的直线
三、两条直线平行的判定方法:
1、定义法:两直线共面且没有公共点。
2、平行线的传递性
3、线面平行的性质定理
4、面面平行的性质定理
5、线面垂直的性质定理
一、直线与平面垂直的性质定理:
垂直于同一个平面的两条直线平行
二、反证法的证明思路:反设→归谬→结论
五、过程设计
(四) 总结反思——提高认识
1、线面垂直的概念
2、如何判定线面垂直?
1、定义
2、判定定理
3、例1的结论
3、在空间,过一点,有几条直线与已知平面垂直?过一点,有几个平面与已知直线垂直?
唯一性公理一
m
A
过一点有且只有一条直线和已知平面垂直
唯一性公理二
过一点有且只有一个平面和已知直线垂直
m
A
B
如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面.
4、我们已经知道:
那么:
如果两条直线同垂直于一个平面,那么这两条直线是否平行?
直线与平面垂直的性质定理:
如果两条直线同垂直于一个平面,
那么这两条直线平行.
3、启发引导—证明定理
A
(1)若a与b相交,
证明:假定b不平行于a,则b与a相交或异面。
过点A有两条直线与平面 垂直
这与“过一点有且只有一条直线垂
直于已知平面”矛盾。
o
(2)若a与b异面,
4、自主探究—深化定理
问题③:
如果两条直线与平面所成的角相等,则两直线平行吗?
结论:平行、相交、异面
a
b
1
2
o1
o2
a
b
A1
A2
1
2
o1
o2
a
1
2
b
o1
o2
a
b
√
×
1、判断下列命题的正误。
(2)垂直于同一直线的两条直线互相平行( )
(3)平行于同一平面的两条直线互相平行( )
(4)垂直于同一平面的两条直线互相平行( )
×
(1)平行于同一直线的两条直线互相平行( )
√
五、过程设计
(三) 线面垂直性质定理的应用
小牛试刀
例1 已知:平面 =AB,PC ,PD ,垂足分
别是C、D,求证: AB CD 。
P
A
B
C
D
H
理论迁移
如图,已知 于点A, 于点B,
求证: .
A
B
C
α
β
l
a
(2)若 ,求证:MN 面PCD
例2 如图,已知 矩形ABCD所在平面,M、N分别是AB、PC的中点求证: (1)
P
A
B
C
D
M
N
E
A
D
C
B
A1
B1
C1
D1
练习:如图,在正方体ABCD-A1B1C1D1中,EF是异面直线AC与A1D的公垂线,求证:EF//BD1.
E
F
提示:异面直线的公垂线是指和两条异面直线都垂直相交的直线
三、两条直线平行的判定方法:
1、定义法:两直线共面且没有公共点。
2、平行线的传递性
3、线面平行的性质定理
4、面面平行的性质定理
5、线面垂直的性质定理
一、直线与平面垂直的性质定理:
垂直于同一个平面的两条直线平行
二、反证法的证明思路:反设→归谬→结论
五、过程设计
(四) 总结反思——提高认识
