高中数学人教A版选修2-1第二章2.1.1曲线与方程课件(22张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-1第二章2.1.1曲线与方程课件(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览






文档简介
2.1曲线与方程
2.1.1 曲线与方程
涪陵第二中学
本节要求
① 理解曲线上的点与方程解之间的一一对应关系。
②初步领会“曲线的方程”与“方程的曲线”的概念。
③强化“形”与“数”一致并相互转化的思想方法。
复习提问
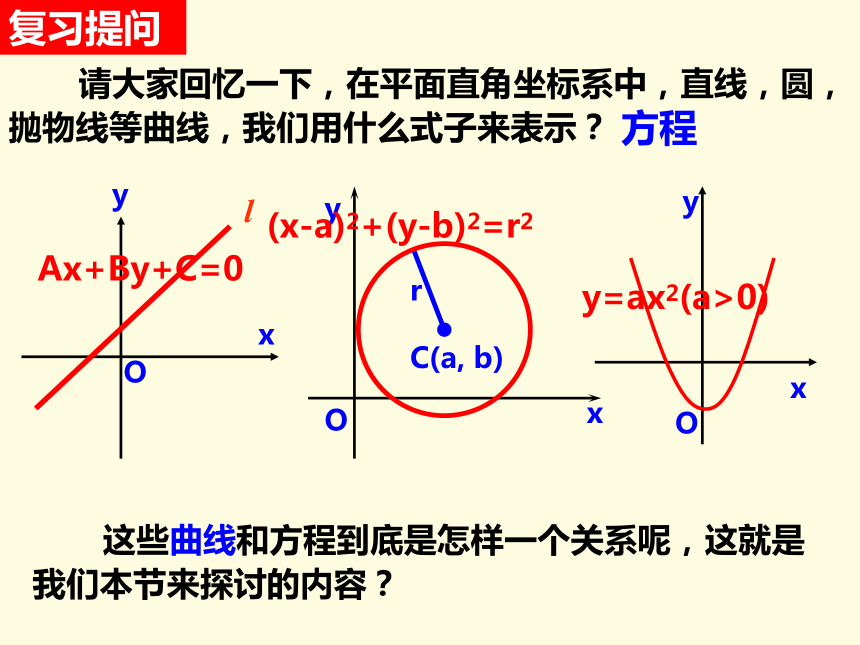
请大家回忆一下,在平面直角坐标系中,直线,圆,抛物线等曲线,我们用什么式子来表示?
O
x
y
l
x
O
y
(x-a)2+(y-b)2=r2
r
C(a, b)
Ax+By+C=0
O
x
y
y=ax2(a>0)
这些曲线和方程到底是怎样一个关系呢,这就是我们本节来探讨的内容?
方程
x
y
0
(1)探求平分一、三象限直线l与方程x-y=0之间的关系?
直线 l上点的横、纵坐标相等
y=x(或x-y=0)
平分一、三象限的直线 l
关系:
x-y=0
(1)直线 l上点的坐标都是方程x-y=0的解;
(2)以方程x-y=0的解为坐标的点都在直线 l上.
曲线
条件
方程
l
●
(x,y)
曲线和方程之间有什么对应关系:
探究新知
(2)探求圆心为(a,b),半径为r的圆与方程(x-a)2 +(y-b)2 =r2之间的关系?
点(x,y)与圆心C(a,b)距离为r
(x-a)2 +(y-b)2 =r2
圆心为(a,b),半径为r的圆C
关系:
(1)圆C上点的坐标都是方程(x-a)2 +(y-b)2 =r2的解;
(2)以方程(x-a)2 +(y-b)2 =r2的解为坐标的点都在圆C上.
曲线
条件
方程
x
O
y
(x-a)2+(y-b)2=r2
r
C(a, b)
●
(x,y)
曲线和方程之间到底是什么样的对应关系呢?
曲线方程的定义
f(x,y)=0
o
x
y
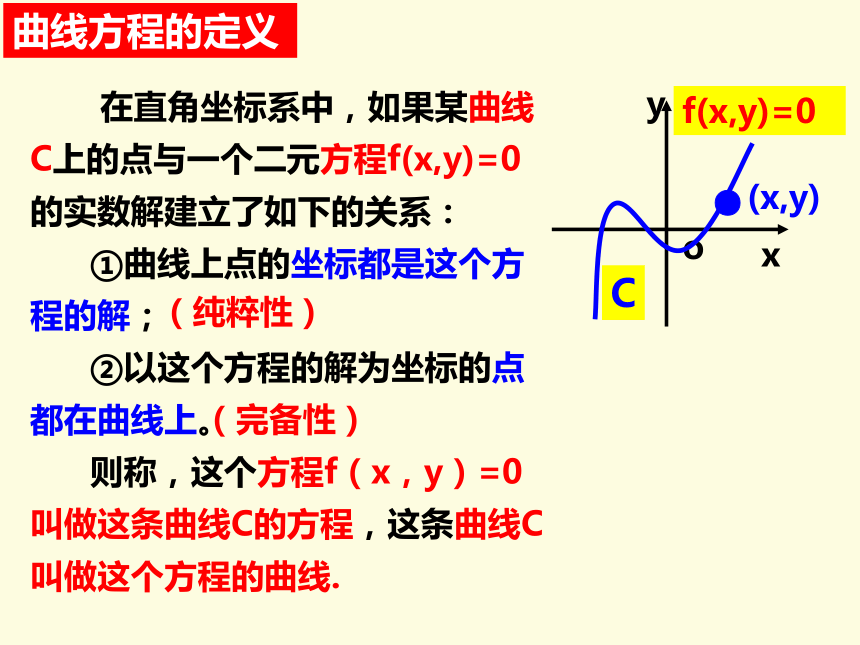
在直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:
①曲线上点的坐标都是这个方程的解;
②以这个方程的解为坐标的点都在曲线上。
则称,这个方程f(x,y)=0叫做这条曲线C的方程,这条曲线C叫做这个方程的曲线.
(纯粹性)
(完备性)
C
●
(x,y)
(1)点集合与解集的对应关系:
无点不是解,无解不是点
点不比解多,解不比点多
(2)点(x0,y0)在曲线C: f(x,y)=0上的充要条件为:
如何理解?
一一对应
(3)曲线的方程:图形所满足的数量关系
方程的曲线:数量关系所表示的图形
f(x,y)=0
o
x
y
C
●
P(x0,y0)
①曲线上点的坐标都是这个方程的解;
②以这个方程的解为坐标的点都在曲线上。
(几何特性)
(代数特性)
例1.(1)说说过A(2,0)平行于y轴的直线m与方程|x|=2的对应关系,并判断直线m的方程是不是|x|=2
1)直线m上的点的坐标都满足方程|x|=2;
2)坐标满足方程|x|=2的点不都在直线m上
结论:
O
x
y
(2,0)
A
直线m的方程不是|x|=2
例析
m
解:
●
(2,y)
●
(-2,y)
O
y
x
A
B
结论:
●
(?,?)
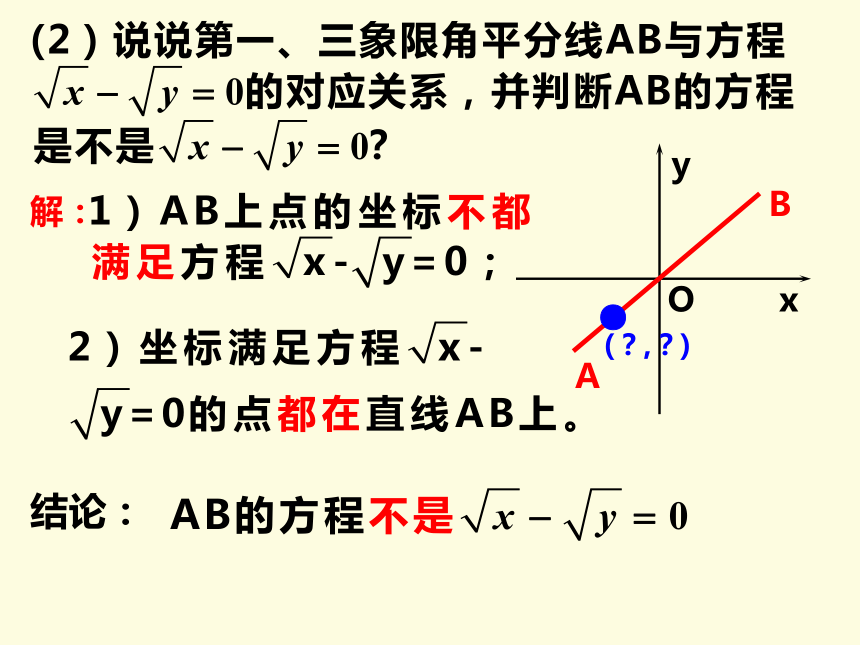
解:
(3) 说说以原点为圆心,半径等于5的圆C与方程是x2 +y2 = 25,的对应关系,并判断圆C的方程是不是x2 +y2 = 25?
1)圆C上点的坐标都满足
即方程x2 +y2 = 25;
2)点坐标满足方程x2 +y2 = 25时,
即这些点都在圆C上.
O
x
y
5
5
结论:
圆C的方程是x2 +y2 = 25.
解:
●
(x,y)
(1)举出一个方程与曲线,使 它们之间的关系符合①而不符合②.
练习
(2)举出一个方程与曲线,使 它们之间的关系符合② 而不符合① .
(3) 举出一个方程与曲线,使 它们之间的关系既符合①又符合②。
①曲线上点的坐标都是这个方程的解(纯粹性);
②以这个方程的解为坐标的点都在曲线上(完备性)。
y
x
8
2
-1
O
(1)符合条件①不符合条件②
① 曲线上点的坐标都是这个方程的解;
② 以这个方程的解为坐标的点都在曲线上。
(-1≤x≤2)
(2)符合条件②不符合条件 ①
① 曲线上点的坐标都是这个方程的解;
② 以这个方程的解为坐标的点都在曲线上。
y
x
8
2
-1
O
(3)符合条件①、 ②
① 曲线上点的坐标都是这个方程的解;
② 以这个方程的解为坐标的点都在曲线上。
x
8
2
-1
y
O
例2.求证:与两坐标轴距离之积等于常数 k(k>0)的点的轨迹的方程是xy=±k
例析
0
y
x
M点与x轴和y轴的距离分别为
1)设M(x0,y0)是轨迹上的任意一点,则
|x0|和|y0|。
∴|x0|?|y0|=k,
即(x0,y0)是xy=±k的解。
即x0?y0=±k
2)设M(x0,y0)坐标是xy=±k的解,则
x0?y0=±k
∴|x0|?|y0|=k
又∵|x0|和|y0|分别是M点与x轴和y轴的距离。
∴M点是轨迹上的点。
由1)2)得,轨迹的方程是xy=±k
解:如图
M(x0,y0)
第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;
证明已知曲线的方程的方法和步骤:
第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.
第三步,由一二步得出结论。
1.? 证明以坐标原点为圆心,半径等于2的圆的方程是x2 +y2 = 4。
(1)设M(x0,y0)是圆上任意一点.
∵点M到坐标原点的距离等于2,
∴ (x0,y0) 是方程x2 +y2 =4的解.
(2)设 (x0,y0) 是方程x2 +y2 = 4的解,则
x02 +y02 = 4,
即点M (x0,y0)到坐标原点的距离等于2,点M (x0,y0)是这个圆上的一点.
由(1)、(2)可知, x2 +y2 = 4是以坐标原点为圆心,半径等于5的圆的方程.
证明:
练习
2.请标出下列方程所对应的曲线
|x|?y=0
x
y
O
y
O
x
x2?y2=0
1
0
x
y
-1
1
x
y
O
0
y
x
1
1
0
y
x
1
1
曲线与方程的内在联系
点M
坐标 (x, y)
曲线C
方程F(x,y)=0
按某种规律运动
(几何意义)
x,y的变化规律及x,y间制约关系
(代数意义)
?
坐标系
曲线与方程的内在联系
对曲线方程的进一步理解
轨迹
图形
小结
1.曲线的方程应满足哪两个条件?怎样理解?
2.如何证明已知曲线的方程?
点
曲线
坐标
方程
3.说说你对这四个词语之间关系的理解。
教材P37:
练习第1,2
习题2.1A组第1题
作业
教材P37
2.1.1 曲线与方程
涪陵第二中学
本节要求
① 理解曲线上的点与方程解之间的一一对应关系。
②初步领会“曲线的方程”与“方程的曲线”的概念。
③强化“形”与“数”一致并相互转化的思想方法。
复习提问
请大家回忆一下,在平面直角坐标系中,直线,圆,抛物线等曲线,我们用什么式子来表示?
O
x
y
l
x
O
y
(x-a)2+(y-b)2=r2
r
C(a, b)
Ax+By+C=0
O
x
y
y=ax2(a>0)
这些曲线和方程到底是怎样一个关系呢,这就是我们本节来探讨的内容?
方程
x
y
0
(1)探求平分一、三象限直线l与方程x-y=0之间的关系?
直线 l上点的横、纵坐标相等
y=x(或x-y=0)
平分一、三象限的直线 l
关系:
x-y=0
(1)直线 l上点的坐标都是方程x-y=0的解;
(2)以方程x-y=0的解为坐标的点都在直线 l上.
曲线
条件
方程
l
●
(x,y)
曲线和方程之间有什么对应关系:
探究新知
(2)探求圆心为(a,b),半径为r的圆与方程(x-a)2 +(y-b)2 =r2之间的关系?
点(x,y)与圆心C(a,b)距离为r
(x-a)2 +(y-b)2 =r2
圆心为(a,b),半径为r的圆C
关系:
(1)圆C上点的坐标都是方程(x-a)2 +(y-b)2 =r2的解;
(2)以方程(x-a)2 +(y-b)2 =r2的解为坐标的点都在圆C上.
曲线
条件
方程
x
O
y
(x-a)2+(y-b)2=r2
r
C(a, b)
●
(x,y)
曲线和方程之间到底是什么样的对应关系呢?
曲线方程的定义
f(x,y)=0
o
x
y
在直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:
①曲线上点的坐标都是这个方程的解;
②以这个方程的解为坐标的点都在曲线上。
则称,这个方程f(x,y)=0叫做这条曲线C的方程,这条曲线C叫做这个方程的曲线.
(纯粹性)
(完备性)
C
●
(x,y)
(1)点集合与解集的对应关系:
无点不是解,无解不是点
点不比解多,解不比点多
(2)点(x0,y0)在曲线C: f(x,y)=0上的充要条件为:
如何理解?
一一对应
(3)曲线的方程:图形所满足的数量关系
方程的曲线:数量关系所表示的图形
f(x,y)=0
o
x
y
C
●
P(x0,y0)
①曲线上点的坐标都是这个方程的解;
②以这个方程的解为坐标的点都在曲线上。
(几何特性)
(代数特性)
例1.(1)说说过A(2,0)平行于y轴的直线m与方程|x|=2的对应关系,并判断直线m的方程是不是|x|=2
1)直线m上的点的坐标都满足方程|x|=2;
2)坐标满足方程|x|=2的点不都在直线m上
结论:
O
x
y
(2,0)
A
直线m的方程不是|x|=2
例析
m
解:
●
(2,y)
●
(-2,y)
O
y
x
A
B
结论:
●
(?,?)
解:
(3) 说说以原点为圆心,半径等于5的圆C与方程是x2 +y2 = 25,的对应关系,并判断圆C的方程是不是x2 +y2 = 25?
1)圆C上点的坐标都满足
即方程x2 +y2 = 25;
2)点坐标满足方程x2 +y2 = 25时,
即这些点都在圆C上.
O
x
y
5
5
结论:
圆C的方程是x2 +y2 = 25.
解:
●
(x,y)
(1)举出一个方程与曲线,使 它们之间的关系符合①而不符合②.
练习
(2)举出一个方程与曲线,使 它们之间的关系符合② 而不符合① .
(3) 举出一个方程与曲线,使 它们之间的关系既符合①又符合②。
①曲线上点的坐标都是这个方程的解(纯粹性);
②以这个方程的解为坐标的点都在曲线上(完备性)。
y
x
8
2
-1
O
(1)符合条件①不符合条件②
① 曲线上点的坐标都是这个方程的解;
② 以这个方程的解为坐标的点都在曲线上。
(-1≤x≤2)
(2)符合条件②不符合条件 ①
① 曲线上点的坐标都是这个方程的解;
② 以这个方程的解为坐标的点都在曲线上。
y
x
8
2
-1
O
(3)符合条件①、 ②
① 曲线上点的坐标都是这个方程的解;
② 以这个方程的解为坐标的点都在曲线上。
x
8
2
-1
y
O
例2.求证:与两坐标轴距离之积等于常数 k(k>0)的点的轨迹的方程是xy=±k
例析
0
y
x
M点与x轴和y轴的距离分别为
1)设M(x0,y0)是轨迹上的任意一点,则
|x0|和|y0|。
∴|x0|?|y0|=k,
即(x0,y0)是xy=±k的解。
即x0?y0=±k
2)设M(x0,y0)坐标是xy=±k的解,则
x0?y0=±k
∴|x0|?|y0|=k
又∵|x0|和|y0|分别是M点与x轴和y轴的距离。
∴M点是轨迹上的点。
由1)2)得,轨迹的方程是xy=±k
解:如图
M(x0,y0)
第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;
证明已知曲线的方程的方法和步骤:
第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.
第三步,由一二步得出结论。
1.? 证明以坐标原点为圆心,半径等于2的圆的方程是x2 +y2 = 4。
(1)设M(x0,y0)是圆上任意一点.
∵点M到坐标原点的距离等于2,
∴ (x0,y0) 是方程x2 +y2 =4的解.
(2)设 (x0,y0) 是方程x2 +y2 = 4的解,则
x02 +y02 = 4,
即点M (x0,y0)到坐标原点的距离等于2,点M (x0,y0)是这个圆上的一点.
由(1)、(2)可知, x2 +y2 = 4是以坐标原点为圆心,半径等于5的圆的方程.
证明:
练习
2.请标出下列方程所对应的曲线
|x|?y=0
x
y
O
y
O
x
x2?y2=0
1
0
x
y
-1
1
x
y
O
0
y
x
1
1
0
y
x
1
1
曲线与方程的内在联系
点M
坐标 (x, y)
曲线C
方程F(x,y)=0
按某种规律运动
(几何意义)
x,y的变化规律及x,y间制约关系
(代数意义)
?
坐标系
曲线与方程的内在联系
对曲线方程的进一步理解
轨迹
图形
小结
1.曲线的方程应满足哪两个条件?怎样理解?
2.如何证明已知曲线的方程?
点
曲线
坐标
方程
3.说说你对这四个词语之间关系的理解。
教材P37:
练习第1,2
习题2.1A组第1题
作业
教材P37
