高中数学选修1-1人教A版:2.3.2直线与抛物线的位置关系课件(26张PPT)
文档属性
| 名称 | 高中数学选修1-1人教A版:2.3.2直线与抛物线的位置关系课件(26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 846.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览





文档简介
(二)归纳:抛物线的几何性质(复习回顾)
图 形
方程
焦点
准线
范围
顶点
对称轴
e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
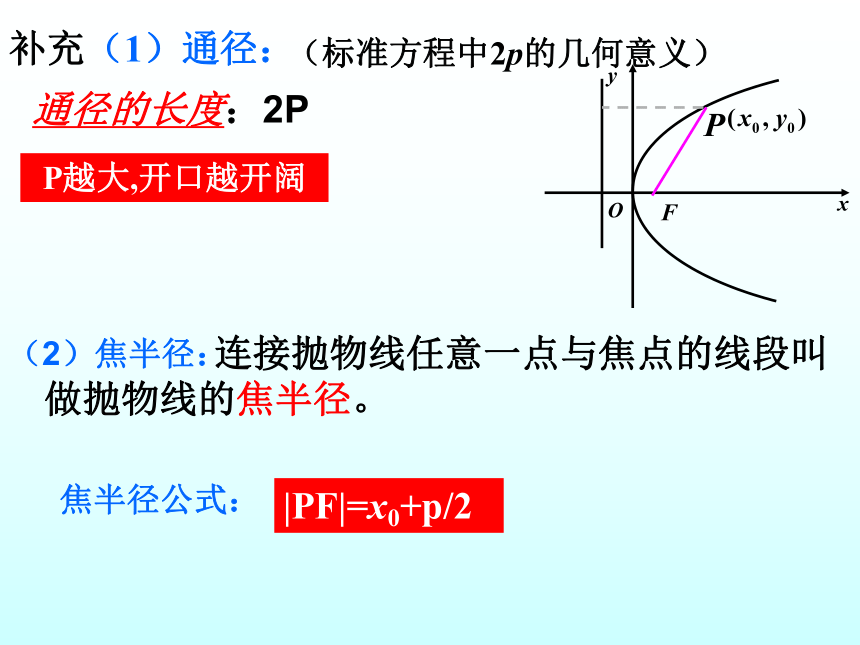
补充(1)通径:
|PF|=x0+p/2
x
O
y
F
P
通径的长度:2P
P越大,开口越开阔
(2)焦半径:
连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。
焦半径公式:
(标准方程中2p的几何意义)
直线与抛物线的位置关系
直线与圆、椭圆、的位置关系的判断方法:
1、根据几何图形判断的直接判断
2、直线与圆锥曲线的公共点的个数
Ax+By+c=0
f(x,y)=0(二次方程)
解的个数
形
数
一、复习引入:
F
x
y
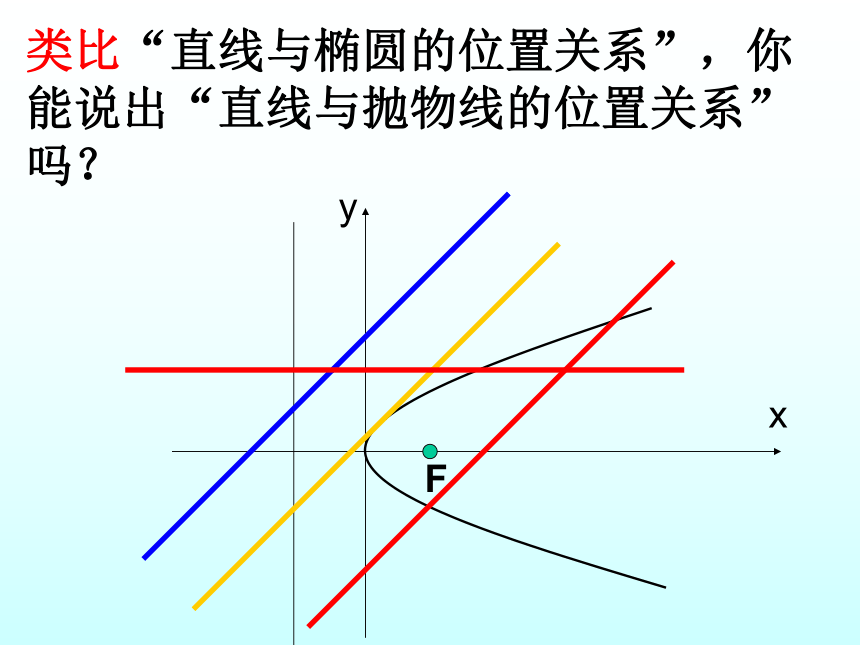
类比“直线与椭圆的位置关系”,你能说出“直线与抛物线的位置关系”吗?
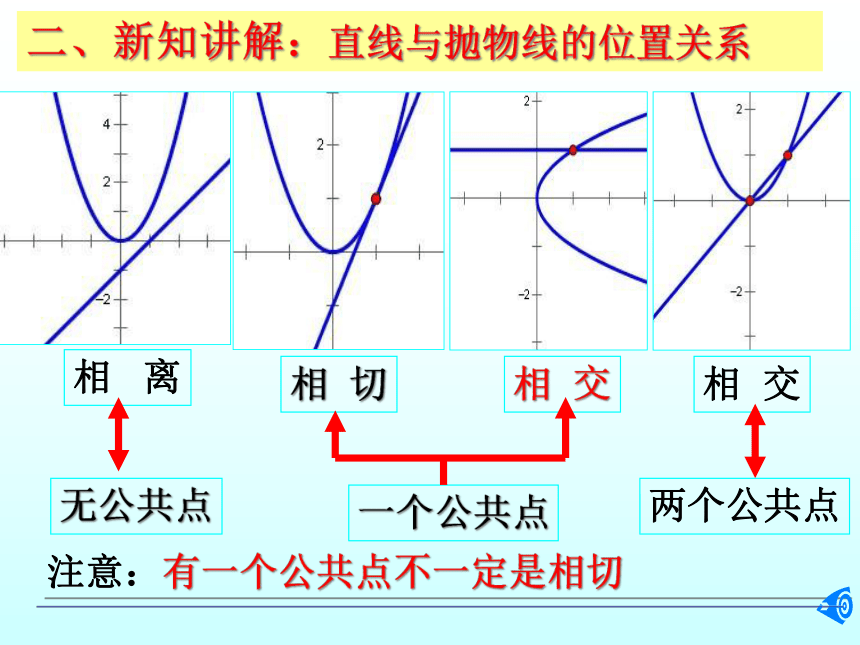
二、新知讲解:直线与抛物线的位置关系
相 离
无公共点
一个公共点
相 切
相 交
相 交
两个公共点
注意:有一个公共点不一定是相切
直线与抛物线的位置关系:
设直线与抛物线方程分别为: y=kx+m与y2=2px:
(1)若直线与对称轴平行或重合,则相交且只有一个交点.
(2)若直线与对称轴相交,
得: Ax2+Bx+C=0
y=kx+m
y2=2px
由
故①△>0
相交
②△=0
相切
③△<0
相离
对于“几何图形观察法”,其优点在于可以根据图形的几何直观直接判断,但由于手工作图会有一定的误差,这对于我们判断结果必定会产生影响.
本节课我们利用解方程组即“代数方法”解决“直线与抛物线公共点个数”的问题.
例1:判断下列直线与抛物线的公共点个数
(1) 与
(2) 与
(3) 与
(4) 与
三、例题讲解
(1)
x
y
(2)
x
y
几 何 法
代 数 法
(3)
(4)
四、新知探究
已知抛物线的方程为 ,动直线
过定点 ,斜率为 .当 为何值
时,直线 与抛物线 :只有一个
公共点;有两个公共点;没有公共点?
代数法
方法:
因为直线过点P(-2,1),斜率为K
利用直线的点斜式方程:
分析:直线与抛物线有一个公共点的情况有两种情形:一种是直线平行于抛物线的对称轴;
另一种是直线与抛物线相切.
联立方程得
公共点的个数
方程组解的个数
消元 方法
整理得
如何求方程①的解呢?
①
我们到底有没有必要求出方程的解呢?
方法探究——代数法
方程①的解的个数
对应的方程组
(*)
①
该方程有几个解呢?
它一定是二次方程吗?
对系数 分类讨论
当 时,方程①为一次方程,此时只有一个解;
当 时,方程①为二次方程,此时需讨论判别式
解:由题意,设直线 的方程为
由方程组
(*)
可得
①
(1)当 时,由方程①得
把 代入 得
这时,直线 与抛物线只有一个公共点
(2)当 时,方程①的判别式为
(Ⅰ)由 即
解得
于是,当 时,方程①只有一个解,从而方
程组(*)只有一个解,这时,直线与抛物线只有一个
公共点.
(Ⅱ)由 即
解得
于是,当 时,方程①有两个解,从而方
程组(*)有两个解.这时,直线与抛物线有两个公共点.
(Ⅲ)由 即
解得
方程组无解,此时直线与抛物线没有交点
综上,我们可得
当 或 或 时,直线 与抛物线
只有一个公共点;
当 ,且 时,直线 与抛物线有两个
公共点;
当 ,或 时,直线 与抛物线没有
公共点;
五、总结提升:
第一步:求出直线 的方程;
第二步:联立直线与抛物线的方程,消元得到
关于 或 的方程 ;
第三步:讨论 的系数 与 的关系.
若 ,则得到一元一次方程;
若 ,则讨论判别式 的符号.
第四步:下结论
六、变式训练
1、已知抛物线的方程为 ,直线
过定点 ,斜率为 .当 为何值
时,直线 与抛物线 :只有一个
公共点;有两个公共点;没有公共点?
2、已知抛物线方程为 ,直线方
程 ,当 为何值时,直线
与抛物线 :只有一个公共点;
有两个公共点;没有公共点?
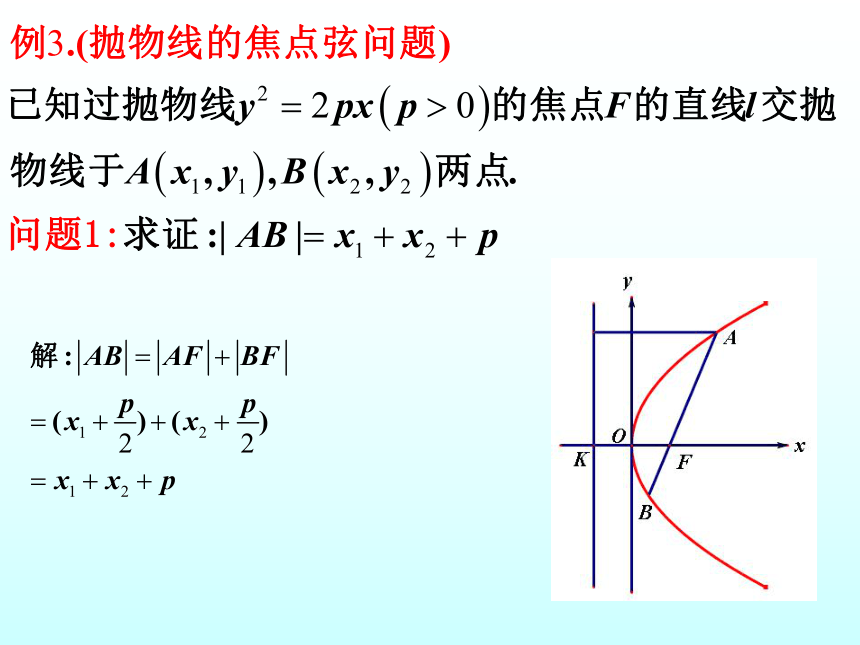
七、思考题:
1、若直线 交抛物线
于 两点,且 ,
求 的值.
2、已知抛物线 ,过点 引弦
,使它恰好被点 平分,求这条弦所
在的直线方程.
1、直线与圆、椭圆、抛物线的位置关系的判断方法:
(1)根据几何图形判断的直接判断
(2)直线与圆锥曲线的公共点的个数
Ax+By+c=0
f(x,y)=0(二次方程)
解的个数
形
数
八、课堂总结
2、判断直线与抛物线位置关系的操作程序
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行
相交(一个点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
图 形
方程
焦点
准线
范围
顶点
对称轴
e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
补充(1)通径:
|PF|=x0+p/2
x
O
y
F
P
通径的长度:2P
P越大,开口越开阔
(2)焦半径:
连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。
焦半径公式:
(标准方程中2p的几何意义)
直线与抛物线的位置关系
直线与圆、椭圆、的位置关系的判断方法:
1、根据几何图形判断的直接判断
2、直线与圆锥曲线的公共点的个数
Ax+By+c=0
f(x,y)=0(二次方程)
解的个数
形
数
一、复习引入:
F
x
y
类比“直线与椭圆的位置关系”,你能说出“直线与抛物线的位置关系”吗?
二、新知讲解:直线与抛物线的位置关系
相 离
无公共点
一个公共点
相 切
相 交
相 交
两个公共点
注意:有一个公共点不一定是相切
直线与抛物线的位置关系:
设直线与抛物线方程分别为: y=kx+m与y2=2px:
(1)若直线与对称轴平行或重合,则相交且只有一个交点.
(2)若直线与对称轴相交,
得: Ax2+Bx+C=0
y=kx+m
y2=2px
由
故①△>0
相交
②△=0
相切
③△<0
相离
对于“几何图形观察法”,其优点在于可以根据图形的几何直观直接判断,但由于手工作图会有一定的误差,这对于我们判断结果必定会产生影响.
本节课我们利用解方程组即“代数方法”解决“直线与抛物线公共点个数”的问题.
例1:判断下列直线与抛物线的公共点个数
(1) 与
(2) 与
(3) 与
(4) 与
三、例题讲解
(1)
x
y
(2)
x
y
几 何 法
代 数 法
(3)
(4)
四、新知探究
已知抛物线的方程为 ,动直线
过定点 ,斜率为 .当 为何值
时,直线 与抛物线 :只有一个
公共点;有两个公共点;没有公共点?
代数法
方法:
因为直线过点P(-2,1),斜率为K
利用直线的点斜式方程:
分析:直线与抛物线有一个公共点的情况有两种情形:一种是直线平行于抛物线的对称轴;
另一种是直线与抛物线相切.
联立方程得
公共点的个数
方程组解的个数
消元 方法
整理得
如何求方程①的解呢?
①
我们到底有没有必要求出方程的解呢?
方法探究——代数法
方程①的解的个数
对应的方程组
(*)
①
该方程有几个解呢?
它一定是二次方程吗?
对系数 分类讨论
当 时,方程①为一次方程,此时只有一个解;
当 时,方程①为二次方程,此时需讨论判别式
解:由题意,设直线 的方程为
由方程组
(*)
可得
①
(1)当 时,由方程①得
把 代入 得
这时,直线 与抛物线只有一个公共点
(2)当 时,方程①的判别式为
(Ⅰ)由 即
解得
于是,当 时,方程①只有一个解,从而方
程组(*)只有一个解,这时,直线与抛物线只有一个
公共点.
(Ⅱ)由 即
解得
于是,当 时,方程①有两个解,从而方
程组(*)有两个解.这时,直线与抛物线有两个公共点.
(Ⅲ)由 即
解得
方程组无解,此时直线与抛物线没有交点
综上,我们可得
当 或 或 时,直线 与抛物线
只有一个公共点;
当 ,且 时,直线 与抛物线有两个
公共点;
当 ,或 时,直线 与抛物线没有
公共点;
五、总结提升:
第一步:求出直线 的方程;
第二步:联立直线与抛物线的方程,消元得到
关于 或 的方程 ;
第三步:讨论 的系数 与 的关系.
若 ,则得到一元一次方程;
若 ,则讨论判别式 的符号.
第四步:下结论
六、变式训练
1、已知抛物线的方程为 ,直线
过定点 ,斜率为 .当 为何值
时,直线 与抛物线 :只有一个
公共点;有两个公共点;没有公共点?
2、已知抛物线方程为 ,直线方
程 ,当 为何值时,直线
与抛物线 :只有一个公共点;
有两个公共点;没有公共点?
七、思考题:
1、若直线 交抛物线
于 两点,且 ,
求 的值.
2、已知抛物线 ,过点 引弦
,使它恰好被点 平分,求这条弦所
在的直线方程.
1、直线与圆、椭圆、抛物线的位置关系的判断方法:
(1)根据几何图形判断的直接判断
(2)直线与圆锥曲线的公共点的个数
Ax+By+c=0
f(x,y)=0(二次方程)
解的个数
形
数
八、课堂总结
2、判断直线与抛物线位置关系的操作程序
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行
相交(一个点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
