高中数学选修2-1人教A版:2.4.2抛物线的简单几何性质(1)课件(28张PPT)
文档属性
| 名称 | 高中数学选修2-1人教A版:2.4.2抛物线的简单几何性质(1)课件(28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 916.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览



文档简介
抛物线的几何性质
(1)
1.抛物线 的焦点坐标是( )。
(A) (B) (C) (D)
x
y
o
x
y
o
y
x
o
y
x
o
【预习检测】
A
D
2.坐标系中,方程
的曲线是( )
(A)
(B)
(C)
(D)
3.动点P到直线x+4=0的距离减它到M(2,0)的距离之差等于2,则P的轨迹是_______________;
其方程为_____________.
抛物线
y2=8x
8
4.过抛物线 的焦点作直线交抛物线于
两点,如果 ,那么
目标
理解并掌握抛物线的简单几何性质
重点
抛物线的几何性质与椭圆、双曲线的比较
难点
能利用抛物线的性质解决有关问题
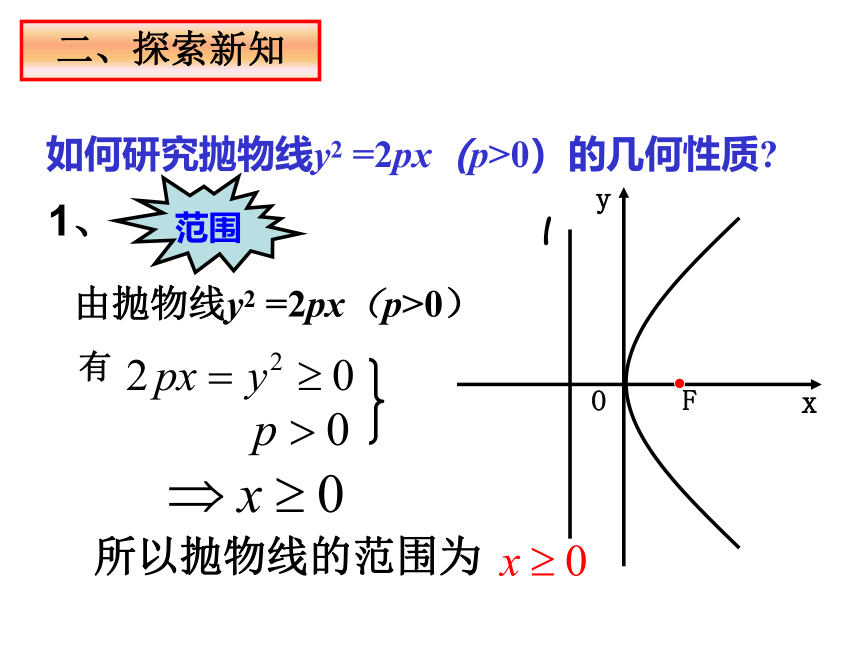
范围
1、
由抛物线y2 =2px(p>0)
有
所以抛物线的范围为
二、探索新知
如何研究抛物线y2 =2px(p>0)的几何性质?
y
F
x
O
l
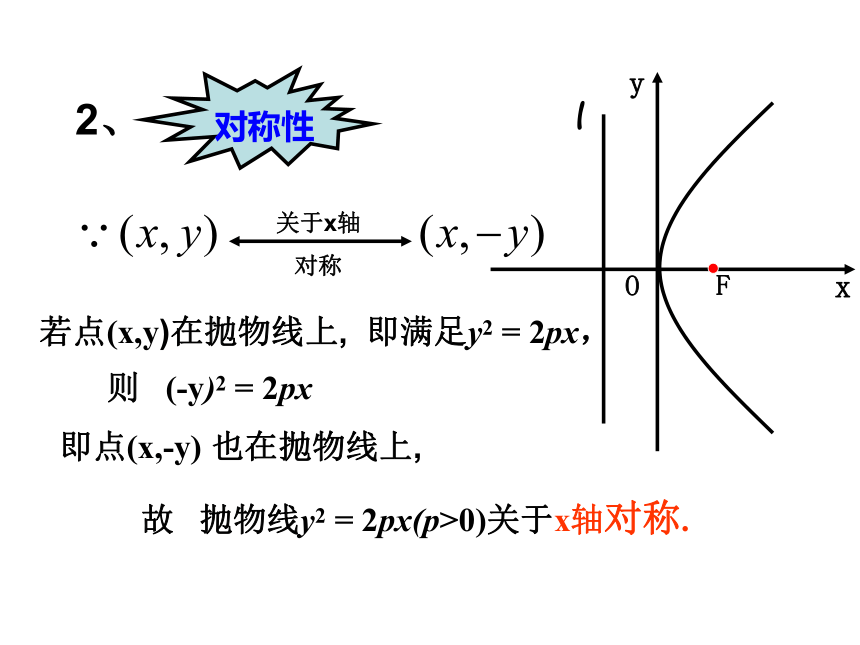
对称性
2、
关于x轴
对称
即点(x,-y) 也在抛物线上,
故 抛物线y2 = 2px(p>0)关于x轴对称.
则 (-y)2 = 2px
若点(x,y)在抛物线上, 即满足y2 = 2px,
y
F
x
O
l
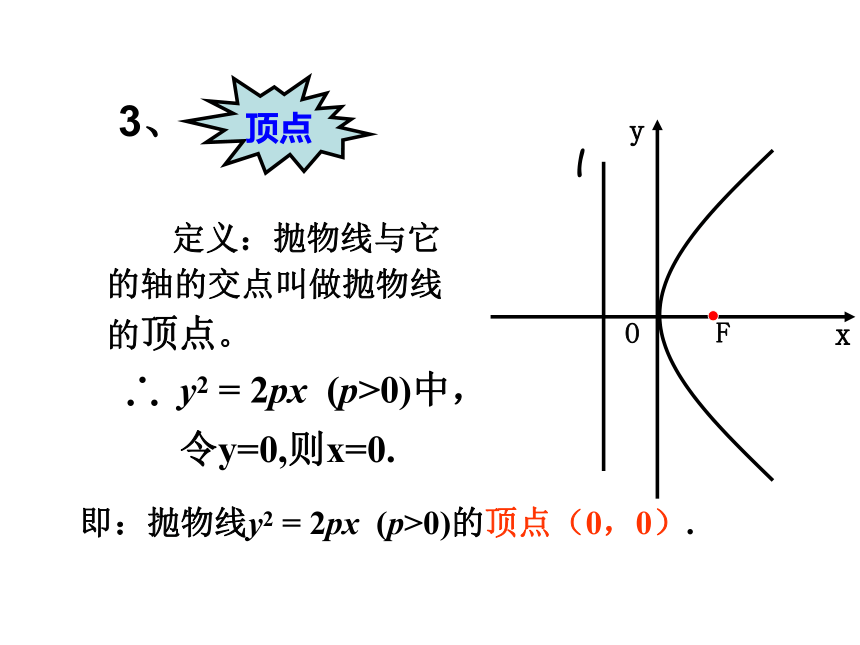
顶点
3、
定义:抛物线与它的轴的交点叫做抛物线的顶点。
y2 = 2px (p>0)中,
令y=0,则x=0.
即:抛物线y2 = 2px (p>0)的顶点(0,0).
y
F
x
O
l
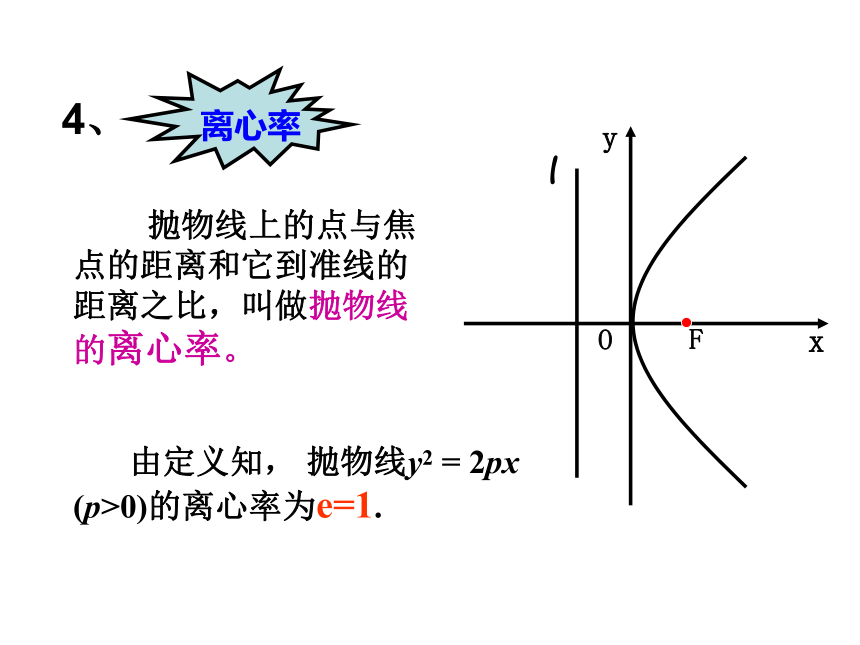
离心率
4、
抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率。
由定义知, 抛物线y2 = 2px (p>0)的离心率为e=1.
y
F
x
O
l
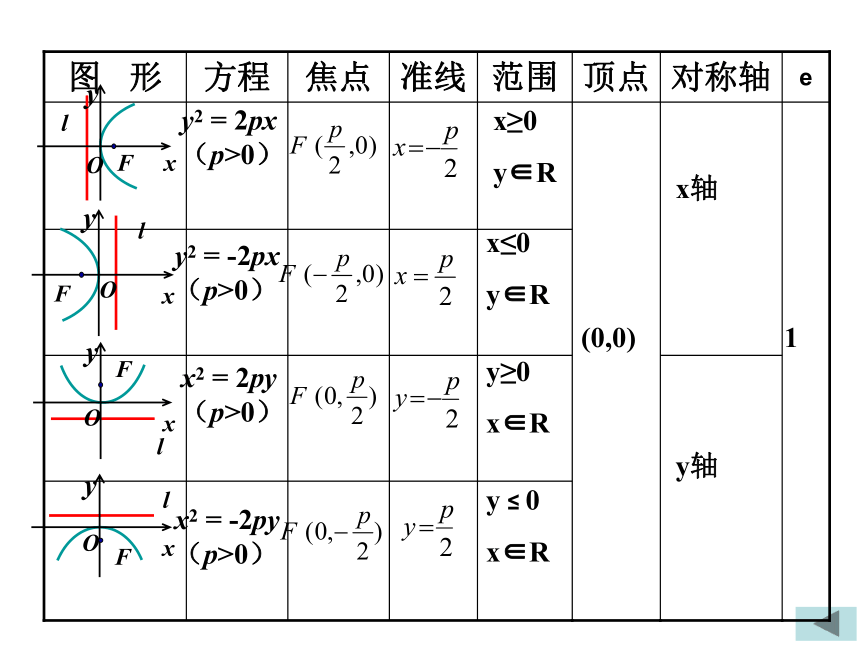
图 形
方程
焦点
准线
范围
顶点
对称轴
e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
x
y
O
F
A
B
y2=2px
2p
过焦点而垂直于对称轴的弦AB,称为抛物线的通径,
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
|AB|=2p
通径
5、
2p越大,抛物线张口越大.
拓展
连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。
|PF|=x0+
焦半径公式:
焦半径
6、
x
y
O
F
P
通过焦点的直线,与抛物
线相交于两点,连接这两点的
线段叫做抛物线的焦点弦。
x
O
y
F
A
焦点弦公式:
B
焦点弦
7、
归纳:
(1)、抛物线可以无限延伸;
(2)、抛物线只有一条对称轴,没有对称中心;
(3)、抛物线只有一个顶点,一个焦点,一条准线;
(4)、抛物线的离心率e是确定的为1,
⑸、抛物线的通径为2P, 2p越大,抛物线的张口越大.
(6)、抛物线的焦半径为
(7)、抛物线的焦点弦为
|PF|=x0+
解法1 F1(1 , 0),
解法2 F1(1 , 0),
解法3 F1(1 , 0),
|AB |= |AF|+ |BF |
= |AA1 |+ |BB1 |
=(x1+1)+(x2+1)
=x1+x2+2=8
A
B
F
A1
B1
解法4
A
B
F
A1
B1
H
同理
引伸: 对于y2=2px(p>0),过焦点F的弦为AB,且
A(x1,y1),B(x2,y2), 则:
O
F
x
y
l
B(x2,y2)
A(x1,y1)
1.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交点为A(x1,y1)、B(x2,y2),则:
提炼总结
(7)以AB为直径的圆与准线l相切.
A1
O
F
x
y
l
B(x2,y2)
A(x1,y1)
B1
(1)
1.抛物线 的焦点坐标是( )。
(A) (B) (C) (D)
x
y
o
x
y
o
y
x
o
y
x
o
【预习检测】
A
D
2.坐标系中,方程
的曲线是( )
(A)
(B)
(C)
(D)
3.动点P到直线x+4=0的距离减它到M(2,0)的距离之差等于2,则P的轨迹是_______________;
其方程为_____________.
抛物线
y2=8x
8
4.过抛物线 的焦点作直线交抛物线于
两点,如果 ,那么
目标
理解并掌握抛物线的简单几何性质
重点
抛物线的几何性质与椭圆、双曲线的比较
难点
能利用抛物线的性质解决有关问题
范围
1、
由抛物线y2 =2px(p>0)
有
所以抛物线的范围为
二、探索新知
如何研究抛物线y2 =2px(p>0)的几何性质?
y
F
x
O
l
对称性
2、
关于x轴
对称
即点(x,-y) 也在抛物线上,
故 抛物线y2 = 2px(p>0)关于x轴对称.
则 (-y)2 = 2px
若点(x,y)在抛物线上, 即满足y2 = 2px,
y
F
x
O
l
顶点
3、
定义:抛物线与它的轴的交点叫做抛物线的顶点。
y2 = 2px (p>0)中,
令y=0,则x=0.
即:抛物线y2 = 2px (p>0)的顶点(0,0).
y
F
x
O
l
离心率
4、
抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率。
由定义知, 抛物线y2 = 2px (p>0)的离心率为e=1.
y
F
x
O
l
图 形
方程
焦点
准线
范围
顶点
对称轴
e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
x
y
O
F
A
B
y2=2px
2p
过焦点而垂直于对称轴的弦AB,称为抛物线的通径,
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
|AB|=2p
通径
5、
2p越大,抛物线张口越大.
拓展
连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。
|PF|=x0+
焦半径公式:
焦半径
6、
x
y
O
F
P
通过焦点的直线,与抛物
线相交于两点,连接这两点的
线段叫做抛物线的焦点弦。
x
O
y
F
A
焦点弦公式:
B
焦点弦
7、
归纳:
(1)、抛物线可以无限延伸;
(2)、抛物线只有一条对称轴,没有对称中心;
(3)、抛物线只有一个顶点,一个焦点,一条准线;
(4)、抛物线的离心率e是确定的为1,
⑸、抛物线的通径为2P, 2p越大,抛物线的张口越大.
(6)、抛物线的焦半径为
(7)、抛物线的焦点弦为
|PF|=x0+
解法1 F1(1 , 0),
解法2 F1(1 , 0),
解法3 F1(1 , 0),
|AB |= |AF|+ |BF |
= |AA1 |+ |BB1 |
=(x1+1)+(x2+1)
=x1+x2+2=8
A
B
F
A1
B1
解法4
A
B
F
A1
B1
H
同理
引伸: 对于y2=2px(p>0),过焦点F的弦为AB,且
A(x1,y1),B(x2,y2), 则:
O
F
x
y
l
B(x2,y2)
A(x1,y1)
1.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交点为A(x1,y1)、B(x2,y2),则:
提炼总结
(7)以AB为直径的圆与准线l相切.
A1
O
F
x
y
l
B(x2,y2)
A(x1,y1)
B1
