高中数学选修2-1人教A版:2.3.2双曲线的渐近线课件(27张PPT)
文档属性
| 名称 | 高中数学选修2-1人教A版:2.3.2双曲线的渐近线课件(27张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 19:18:17 | ||
图片预览








文档简介
关于x轴、y轴、原点对称
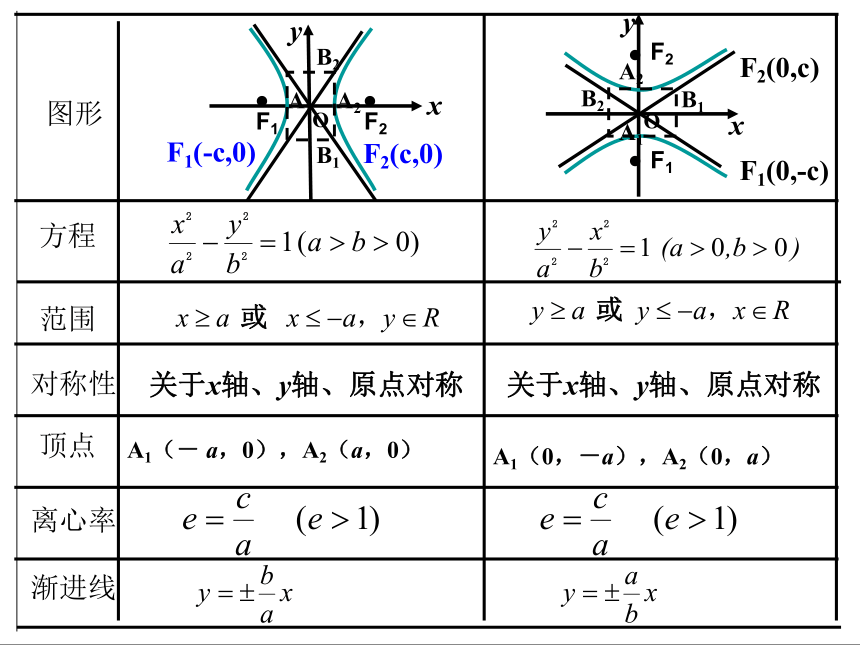
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐进线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
能不能直接由双曲线方程推出渐近线方程?
结论:
双曲线方程
中,把1改为0,得
由双曲线方程求渐近线方程的方法:
______________________________________
______________________________________
(1) 定焦点位置,求出 a、b,写出方程
(2) 由双曲线方程的常数项令为零即可
若渐近线方程为 mx ±ny = 0,则双曲线方程
为 ____________________________
或 ____________________________
m 2 x 2 -n 2 y 2 = k ( k ≠ 0 )
整式
标准
例1.已知双曲线的焦点在x轴上,中心在原点,如果焦距为8,实轴长为6,求此双曲线的标准方程及其渐近线的方程。
练习、求下列双曲线的渐近线方程
(1)4x2-9y2=36,
(2)25x2-4y2=100.
2x±3y=0
5x±2y=0
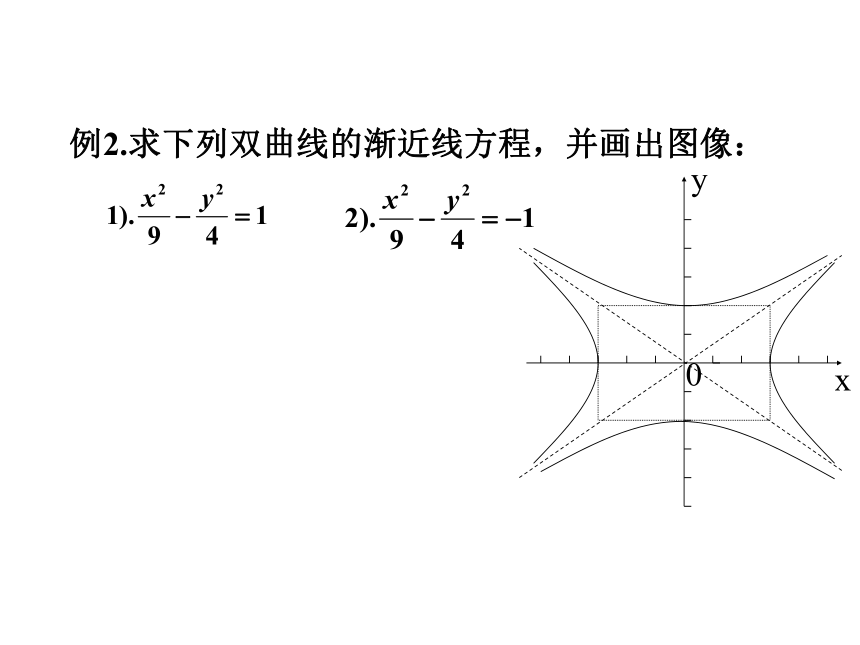
例2.求下列双曲线的渐近线方程,并画出图像:
0
x
y
例3 求与双曲线 共渐近线且过点
的双曲线方程及离心率.
解:
设与已知双曲线共渐近线的双曲线方程为
∵ 点 在双曲线上,
故所求双曲线方程为:
即
∴ 离心率
例4.已知双曲线的渐近线是x±2y=0 ,并且双曲线过点 求双曲线方程。
变形:已知双曲线渐近线是x±2y=0 ,并且双曲线过点 求双曲线方程。
例5.已知双曲线的渐近线方程为y=± ,并且焦点都在圆x2+y2=100上,求双曲线的方程。
解:当焦点在x轴上时,设双曲线的方程是
因为焦点都在圆x2+y2=100上,所以c=10,
又双曲线的渐近线方程为y=±
所以
由
解得
所以双曲线的方程是
当焦点在y轴上时,设双曲线的方程是
因为焦点都在圆x2+y2=100上,
所以c=10,
又双曲线的渐近线方程为y=±
所以
解得
所以双曲线的方程是
由
例5.已知双曲线的方程渐近线为
上,求双曲线方程.
并且焦点都在圆
解:
∵ 双曲线的方程渐近线为
∴ 可双曲线方程为:
∵焦点都在圆
上,
∴所求双曲线方程:
即
[练一练]
双曲线的两条渐近线的夹角为60°,则双曲线的
离心率为_______.
【解析】渐近线斜率是 而夹角是60°.因为两直线关于x
轴对称,所以和x轴夹角是30°或60°.即
或 若
若 b2=3a2,c2=a2+b2=4a2,e2=4,e=2.
答案:2或
5分)设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使|A1B1|=|A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A.(
,2] B.[
,2)
D.[
,+∞)
C.(
,+∞) D.[
【解析】选A.设双曲线的焦点在x轴上,则由作图易知双曲线的渐近线的斜率
必须满足
所以
即有
又双曲线的离心率为
所以
过一定点与双曲线仅有一个公共点的直线条数,与这个定点的位置有关:
(1)当点在渐近线上时有0条或2条(为中心时有0条,其余有2条);
(2)当点在双曲线上时有3条;
(3)当点在双曲线内部时有2条;
(4)其余均为4条。
解题归纳
变式2:
过定点P(0,-1)的直线与双曲线 仅有一个公共点的直线有( )条。
过定点P(2,1)的直线与双曲线 仅有一个公共点的直线有( )条。
变式1
4
4
变式2
过定点P(3,1)的直线与双曲线 仅有一个公共点的直线有( )条。
2
过定点P(1,1)的直线与双曲线 仅有一个公共点的直线有( )条。
2
变式3
归纳:过一定点与双曲线仅有一个公共点的直线的条数——数形结合,相切或与渐近线平行。
变式4
3
过定点 的直线与双曲线 仅有一个公共点的直线有( )条。
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐进线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
能不能直接由双曲线方程推出渐近线方程?
结论:
双曲线方程
中,把1改为0,得
由双曲线方程求渐近线方程的方法:
______________________________________
______________________________________
(1) 定焦点位置,求出 a、b,写出方程
(2) 由双曲线方程的常数项令为零即可
若渐近线方程为 mx ±ny = 0,则双曲线方程
为 ____________________________
或 ____________________________
m 2 x 2 -n 2 y 2 = k ( k ≠ 0 )
整式
标准
例1.已知双曲线的焦点在x轴上,中心在原点,如果焦距为8,实轴长为6,求此双曲线的标准方程及其渐近线的方程。
练习、求下列双曲线的渐近线方程
(1)4x2-9y2=36,
(2)25x2-4y2=100.
2x±3y=0
5x±2y=0
例2.求下列双曲线的渐近线方程,并画出图像:
0
x
y
例3 求与双曲线 共渐近线且过点
的双曲线方程及离心率.
解:
设与已知双曲线共渐近线的双曲线方程为
∵ 点 在双曲线上,
故所求双曲线方程为:
即
∴ 离心率
例4.已知双曲线的渐近线是x±2y=0 ,并且双曲线过点 求双曲线方程。
变形:已知双曲线渐近线是x±2y=0 ,并且双曲线过点 求双曲线方程。
例5.已知双曲线的渐近线方程为y=± ,并且焦点都在圆x2+y2=100上,求双曲线的方程。
解:当焦点在x轴上时,设双曲线的方程是
因为焦点都在圆x2+y2=100上,所以c=10,
又双曲线的渐近线方程为y=±
所以
由
解得
所以双曲线的方程是
当焦点在y轴上时,设双曲线的方程是
因为焦点都在圆x2+y2=100上,
所以c=10,
又双曲线的渐近线方程为y=±
所以
解得
所以双曲线的方程是
由
例5.已知双曲线的方程渐近线为
上,求双曲线方程.
并且焦点都在圆
解:
∵ 双曲线的方程渐近线为
∴ 可双曲线方程为:
∵焦点都在圆
上,
∴所求双曲线方程:
即
[练一练]
双曲线的两条渐近线的夹角为60°,则双曲线的
离心率为_______.
【解析】渐近线斜率是 而夹角是60°.因为两直线关于x
轴对称,所以和x轴夹角是30°或60°.即
或 若
若 b2=3a2,c2=a2+b2=4a2,e2=4,e=2.
答案:2或
5分)设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使|A1B1|=|A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A.(
,2] B.[
,2)
D.[
,+∞)
C.(
,+∞) D.[
【解析】选A.设双曲线的焦点在x轴上,则由作图易知双曲线的渐近线的斜率
必须满足
所以
即有
又双曲线的离心率为
所以
(1)当点在渐近线上时有0条或2条(为中心时有0条,其余有2条);
(2)当点在双曲线上时有3条;
(3)当点在双曲线内部时有2条;
(4)其余均为4条。
解题归纳
变式2:
过定点P(0,-1)的直线与双曲线 仅有一个公共点的直线有( )条。
过定点P(2,1)的直线与双曲线 仅有一个公共点的直线有( )条。
变式1
4
4
变式2
过定点P(3,1)的直线与双曲线 仅有一个公共点的直线有( )条。
2
过定点P(1,1)的直线与双曲线 仅有一个公共点的直线有( )条。
2
变式3
归纳:过一定点与双曲线仅有一个公共点的直线的条数——数形结合,相切或与渐近线平行。
变式4
3
过定点 的直线与双曲线 仅有一个公共点的直线有( )条。
