高中数学选修2-1人教A版:2.3.2直线与双曲线的位置关系课件 (1)(48张PPT)
文档属性
| 名称 | 高中数学选修2-1人教A版:2.3.2直线与双曲线的位置关系课件 (1)(48张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 19:48:00 | ||
图片预览








文档简介
直线与双曲线的位置关系
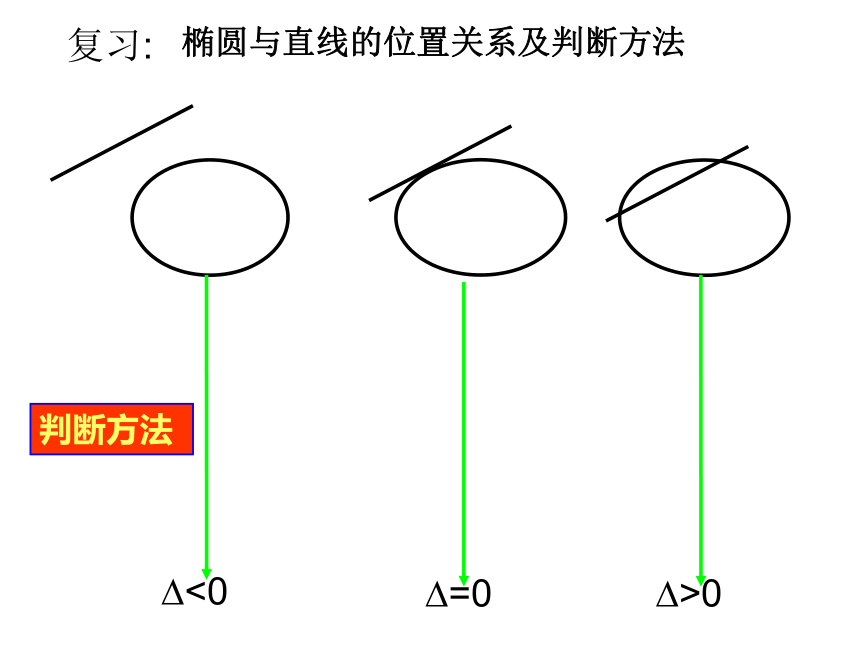
椭圆与直线的位置关系及判断方法
判断方法
?<0
?=0
?>0
(1)联立方程组
(2)消去一个未知数
(3)
复习:
相离
相切
相交
含焦点区域外
含焦点区域内
含焦点区域内
P
P
P
当点P在双曲线上时,能作3条直线与双曲线只有一个公共点。
P
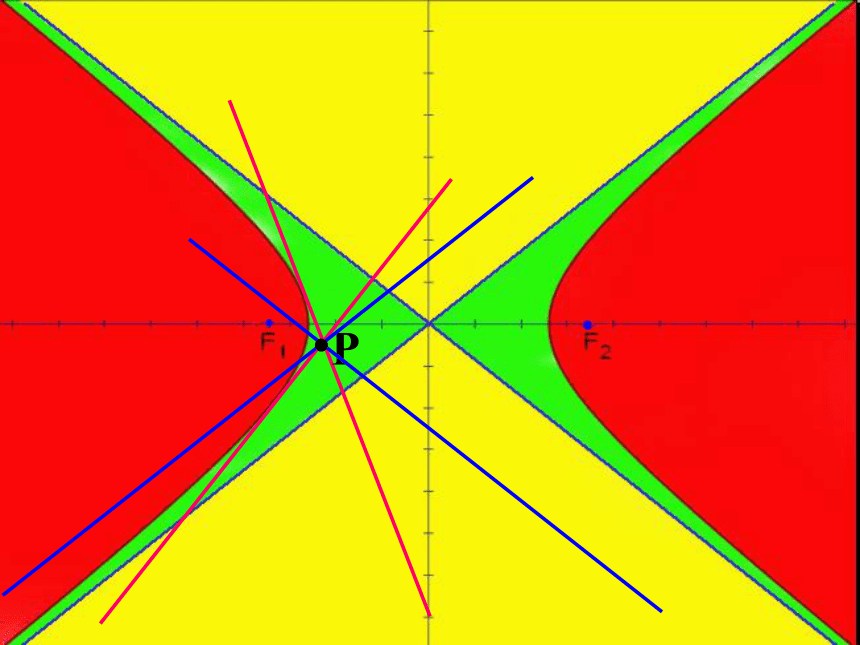
当点P在其中一条渐近线上(中心除外)时,一条是切线,一条是与另一条渐近线平行。
P
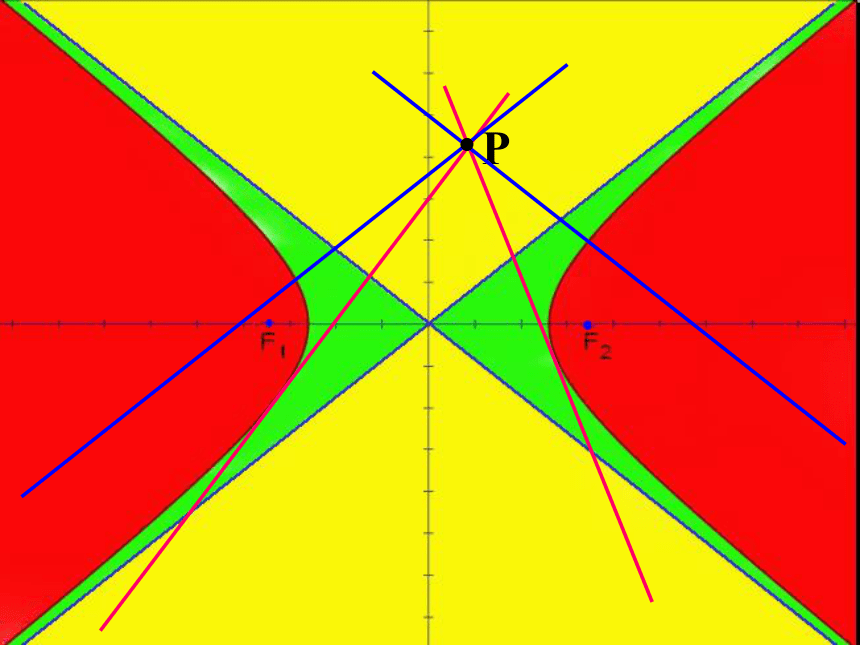
当点P在含焦点区域内时,两条是分别与两条渐近线平行。
P
当点P在双曲线的中心时,不可能作出一条直线与双曲线只有一个公共点。
过点P且与双曲线只有一个公共点的直线最多有4条
也就是说过点P作与双曲线只有一个公共点的直线条数可能是4条、3条、2条、0条
(b2-a2k2)x2-2kma2x+a2(m2+b2)=0
1.二次项系数为0时,直线L(K= )与双曲线的渐近线平行或重合。
重合:无交点;平行:有一个交点。
2.二次项系数不为0时,上式为一元二次方程,
Δ>0 直线与双曲线相交(两个交点)
Δ=0 直线与双曲线相切
Δ<0 直线与双曲线相离
理论分析:
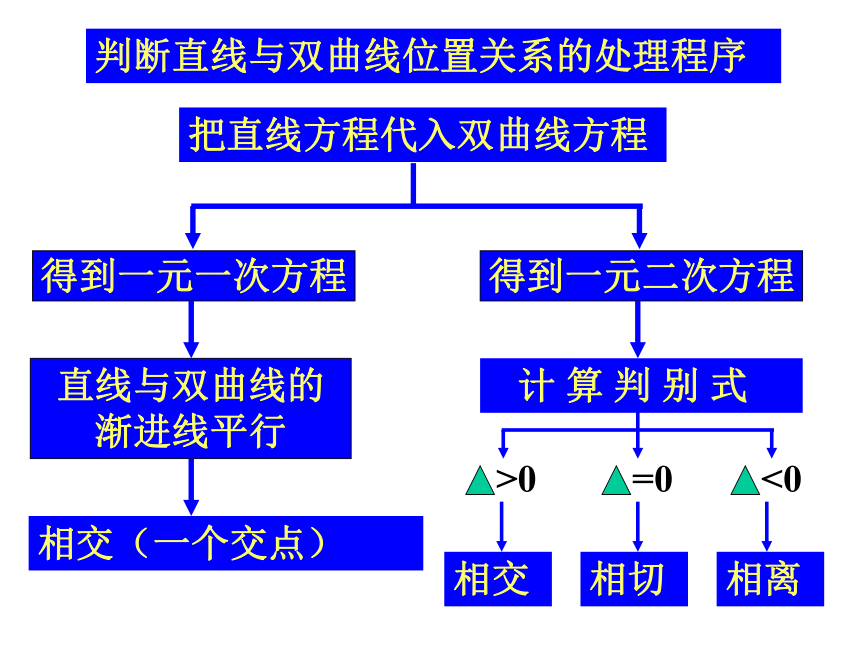
判断直线与双曲线位置关系的处理程序
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
特别注意:
直线与双曲线的位置关系中:
一解不一定相切,相交不一定两解,两解不一定同支
2.过点P(1,1)与双曲线
只有
共有_______条.
变式:将点P(1,1)改为
1.A(3,4)
2.B(3,0)
3.C(4,0)
4.D(0,0).答案又是怎样的?
4
1.两条;2.三条;3.两条;4.零条.
交点的
一个
直线
X
Y
O
(1,1)
。
例题讲解
例3:如果直线y=kx-1与双曲线x2-y2=4没有公共点,求k的取值范围
解:由 得(1-k2)x2+2kx-5=0(*) 即方程无解
y=kx-1
x2-y2=4
∴
1-k2≠0
△=4k2+20(1-k2)<0
k> 或k< -
∴ k> 或k< -
引申1:如果直线y=kx-1与双曲线x2-y2=4有两个公共点,求k的取值范围
解:直线一双曲线有两个公共点 方程(*)有两个不等的根
1-k2≠0
△=4k2+20(1-k2)>0
-∴
-思考?
2、如果直线y=kx-1与双曲线x2-y2=4右支有两个公共点,求k的取值范围
3、如果直线y=kx-1与双曲线x2-y2=4左支有两个公共点,求k的取值范围
4、如果直线y=kx-1与双曲线x2-y2=4左、右支各1个公共点,求k的取值范围
1、如果直线y=kx-1与双曲线x2-y2=4只有1个公共点,求k的取值范围
解:等价于(*)只有一解。①当1-k2=0时,即k= 1(*)只有一解
② 当1-k2≠0时,△=0,即k= (*)只有一解
x1x2= - >0
解:等价于
4k2+20(1-k2)>0
x1+x2= - 2 >0
1-k2≠0
2
2
1x1x2= - >0
解:等价于
4k2+20(1-k2)>0
x1+x2= - 2 <0
1-k2≠0
2
2
-解:等价于
1-k2≠0
4k2+20(1-k2)>0
x1x2= - <0
2
-1 要使直线与双曲线的右支有两个 相异的公共点,则应满足
(2)解:将直线 代入双曲线方程
化简整理
(※)
解得
注: 直线与 双曲线的右支有两个交点,实际上给出了 方程 解的范围,涉及到二次方程的根的分布问题.解题时需要注意!
由韦达定理得:
例4.以P(1,8)为中点作双曲线为y2-4x2=4的一条
弦AB,求直线AB的方程。
典型例题:
解法一:
(1) 当过P点的直线AB和x轴垂直时,直线被双曲线
截得的弦的中点不是P点。
(2) 当过P点的直线AB和x轴不垂直时,设其斜率为k.
则直线AB的方程为y-8=k(x-1)
例4.以P(1,8)为中点作双曲线为y2-4x2=4的一条
弦AB,求直线AB的方程。
3.过原点与双曲线 交于两点的直线斜率的
取值范围是
解:将y=ax+1代入3x2-y2=1
又设方程的两根为x1,x2,A(x1,y1),B(x2,y2),
得(3-a2)x2-2ax-2=0,
它有两个实根,必须△>0,
∵原点O(0,0)在以AB为直径的圆上,
例6、直线y-ax-1=0和曲线3x2-y2=1相交,交点为
A、B,当a为何值时,以AB为直径的圆经过坐
标原点。
典型例题:
解:将y=ax+1代入3x2-y2=1
又设方程的两根为x1,x2,A(x1,y1),B(x2,y2),
得(3-a2)x2-2ax-2=0,
它有两个实根,必须△>0,
∵原点O(0,0)在以AB为直径的圆上,
∴OA⊥OB,即x1x2+y1y2=0,
即x1x2+(ax1+1)(ax2+1)=0,
∴(a2+1) x1x2 +a(x1+x2 )+1=0,
解得a=±1.
2、过双曲线 的右焦点 倾斜角为
的直线交双曲线于A,B两点,求|AB|。
作业:
椭圆与直线的位置关系及判断方法
判断方法
?<0
?=0
?>0
(1)联立方程组
(2)消去一个未知数
(3)
复习:
相离
相切
相交
含焦点区域外
含焦点区域内
含焦点区域内
P
P
P
当点P在双曲线上时,能作3条直线与双曲线只有一个公共点。
P
当点P在其中一条渐近线上(中心除外)时,一条是切线,一条是与另一条渐近线平行。
P
当点P在含焦点区域内时,两条是分别与两条渐近线平行。
P
当点P在双曲线的中心时,不可能作出一条直线与双曲线只有一个公共点。
过点P且与双曲线只有一个公共点的直线最多有4条
也就是说过点P作与双曲线只有一个公共点的直线条数可能是4条、3条、2条、0条
(b2-a2k2)x2-2kma2x+a2(m2+b2)=0
1.二次项系数为0时,直线L(K= )与双曲线的渐近线平行或重合。
重合:无交点;平行:有一个交点。
2.二次项系数不为0时,上式为一元二次方程,
Δ>0 直线与双曲线相交(两个交点)
Δ=0 直线与双曲线相切
Δ<0 直线与双曲线相离
理论分析:
判断直线与双曲线位置关系的处理程序
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
特别注意:
直线与双曲线的位置关系中:
一解不一定相切,相交不一定两解,两解不一定同支
2.过点P(1,1)与双曲线
只有
共有_______条.
变式:将点P(1,1)改为
1.A(3,4)
2.B(3,0)
3.C(4,0)
4.D(0,0).答案又是怎样的?
4
1.两条;2.三条;3.两条;4.零条.
交点的
一个
直线
X
Y
O
(1,1)
。
例题讲解
例3:如果直线y=kx-1与双曲线x2-y2=4没有公共点,求k的取值范围
解:由 得(1-k2)x2+2kx-5=0(*) 即方程无解
y=kx-1
x2-y2=4
∴
1-k2≠0
△=4k2+20(1-k2)<0
k> 或k< -
∴ k> 或k< -
引申1:如果直线y=kx-1与双曲线x2-y2=4有两个公共点,求k的取值范围
解:直线一双曲线有两个公共点 方程(*)有两个不等的根
1-k2≠0
△=4k2+20(1-k2)>0
-
-
2、如果直线y=kx-1与双曲线x2-y2=4右支有两个公共点,求k的取值范围
3、如果直线y=kx-1与双曲线x2-y2=4左支有两个公共点,求k的取值范围
4、如果直线y=kx-1与双曲线x2-y2=4左、右支各1个公共点,求k的取值范围
1、如果直线y=kx-1与双曲线x2-y2=4只有1个公共点,求k的取值范围
解:等价于(*)只有一解。①当1-k2=0时,即k= 1(*)只有一解
② 当1-k2≠0时,△=0,即k= (*)只有一解
x1x2= - >0
解:等价于
4k2+20(1-k2)>0
x1+x2= - 2 >0
1-k2≠0
2
2
1
解:等价于
4k2+20(1-k2)>0
x1+x2= - 2 <0
1-k2≠0
2
2
-
1-k2≠0
4k2+20(1-k2)>0
x1x2= - <0
2
-1
(2)解:将直线 代入双曲线方程
化简整理
(※)
解得
注: 直线与 双曲线的右支有两个交点,实际上给出了 方程 解的范围,涉及到二次方程的根的分布问题.解题时需要注意!
由韦达定理得:
例4.以P(1,8)为中点作双曲线为y2-4x2=4的一条
弦AB,求直线AB的方程。
典型例题:
解法一:
(1) 当过P点的直线AB和x轴垂直时,直线被双曲线
截得的弦的中点不是P点。
(2) 当过P点的直线AB和x轴不垂直时,设其斜率为k.
则直线AB的方程为y-8=k(x-1)
例4.以P(1,8)为中点作双曲线为y2-4x2=4的一条
弦AB,求直线AB的方程。
3.过原点与双曲线 交于两点的直线斜率的
取值范围是
解:将y=ax+1代入3x2-y2=1
又设方程的两根为x1,x2,A(x1,y1),B(x2,y2),
得(3-a2)x2-2ax-2=0,
它有两个实根,必须△>0,
∵原点O(0,0)在以AB为直径的圆上,
例6、直线y-ax-1=0和曲线3x2-y2=1相交,交点为
A、B,当a为何值时,以AB为直径的圆经过坐
标原点。
典型例题:
解:将y=ax+1代入3x2-y2=1
又设方程的两根为x1,x2,A(x1,y1),B(x2,y2),
得(3-a2)x2-2ax-2=0,
它有两个实根,必须△>0,
∵原点O(0,0)在以AB为直径的圆上,
∴OA⊥OB,即x1x2+y1y2=0,
即x1x2+(ax1+1)(ax2+1)=0,
∴(a2+1) x1x2 +a(x1+x2 )+1=0,
解得a=±1.
2、过双曲线 的右焦点 倾斜角为
的直线交双曲线于A,B两点,求|AB|。
作业:
