沪教版高中数学高二第二学期11.1直线与方程复习 课件(32张PPT)
文档属性
| 名称 | 沪教版高中数学高二第二学期11.1直线与方程复习 课件(32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 777.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览











文档简介
第一课:直线的方程
一、直线的方程
k是直线的斜率,
b:直线在y轴上的截距
1、直线的斜截式方程
y=kx+b (k∈R)叫做直线的斜截式方程
直线过点(0,b)
x
y
o
已知直线l经过点P(x0,y0),并且与向量 平行,则直线l的方程
2、直线点方向式方程
x
y
o
3、直线的点法向式
已知直线l经过点P(x0,y0), 并且与向 量 垂直,求直线的方程
直线的点法向式方程
4、直线的一般式方程
5、直线的点斜式方程
6、直线的截距式方程
1、定义:①当直线l与x轴相交与M,我们将x轴绕着交点M按逆时针方向旋转到与l重合时所旋转的最小正角α叫做直线的倾斜角 。
2、范围: 0≤α<π。
3、任何一条直线都有倾斜角直线的倾斜角决定直线的方向。
②当直线l与x轴平行或重合时,规定直线的倾斜角 α=0
二、直线的倾斜角、斜率
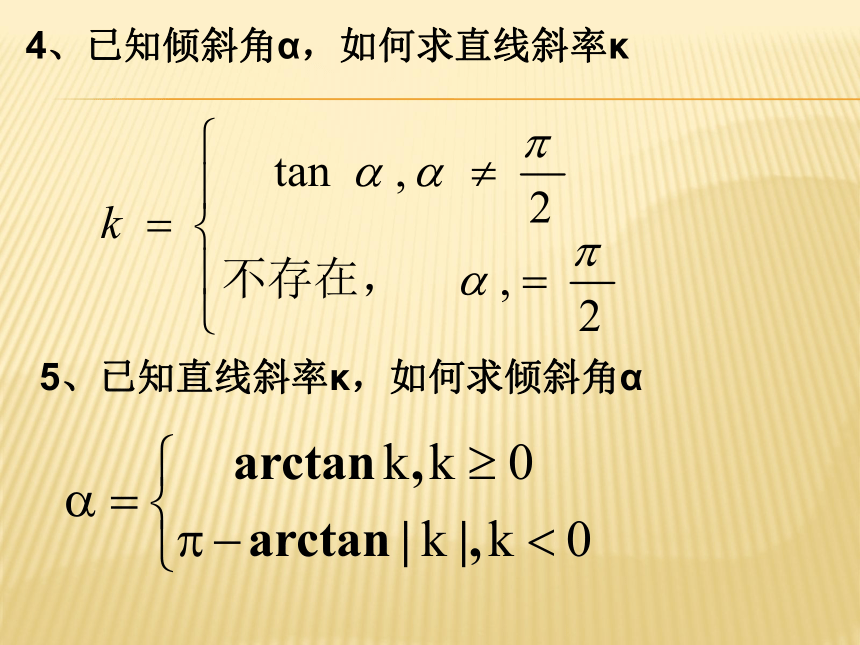
4、已知倾斜角α,如何求直线斜率κ
5、已知直线斜率κ,如何求倾斜角α
α
k
o
三:直线的方向向量、法向量、斜率、倾斜角
法向量
方向向量
斜 率
倾斜角
坐标平面上的直线
第二课:
两直线的位置关系
相交
D≠0时,方程组有唯一解
X=Dx/D y=Dy/D
平行
D=0,Dx≠0或Dy≠0时方程组无解
重合
D=0,Dx=Dy=0时方程组有无数解
1、两直线的位置关系
设直线l1和l2的斜率为k1和k2,则“l1⊥l2 ”是
“k1·k2 =-1”充要条件
2、直线的平行
3、直线的垂直
设直线l1、l2的夹角为α,则
4、直线的夹角公式
O
x
y
点 到直线 的距离:
5、点到直线的距离
特殊地:
设点P(x,y),则
P到x轴的距离为
_______;
P到y轴的距离为
_______;
P到直线x-a=0的距离为
_______;
P到直线y-b=0的距离为
_______;
x
|y|
|x|
|x-a|
|y-b|
已知两条平行直线
l1:Ax+By+C1=0. l2:Ax+By+C2=0.
则两条平行直线的距离d为:
6、两条平行直线的距离
已知直线l:ax+by+c=0.点A(x1,y1)、B(x2,y2)则
(1)、A、B在直线同侧的充要条件为
(ax1+by1+c)· (ax2+by2+c)>0
(2)、A、B在直线异侧的充要条件为
(ax1+by1+c)· (ax2+by2+c)<0
(3)、直线与线段AB相交的充要条件为
(ax1+by1+c)· (ax2+by2+c)≤0
7、两直线与线段相交
课堂练习:(1)如果A(3, 1)、B(-2, k)、
C(8, 11),在同一直线上,那么k 的值是( )
(A)-6 (B)-7 (C)-8 (D)-9
(2)如果直线通过点(-1,-3), 并且与x轴平行,那么的方程是( )。
(A)y+3=0 (B)y-3=0
(C)x+1=0 (D)x-1=0
D
A
小结:证明三点共线的方法--斜率相等法,
直线方程法, 向量平行法, 线段相等法。
若将此题中的平行改为垂直,答案怎样?
练习2:
A、平行 B、重合 C、垂直 D相交但不垂直
C
、直线L过点A(2,3),且被两平行线L1:3x+4y-7=0和L2:3x+4y+8=0截得的线段长为 ,试求直线的方程
练习3:
练习4、一直线被两直线L1:4x+y+6=0,L2:3x-5y-6=0截得的线段的中点恰好是坐标原点,求该直线方程
5、在三角形ABC中,BC边上的高所在直线的方程为x-2y+1=0,A的平分线所在直线的方程为y=0,若B点的坐标为(1,2),求点A和点C的坐标
6、已知三角形ABC的一条内角平分线CD的方程是2x+y-1=0,两个顶点A(1,2) B(-1,-1),求第三个顶点C的坐标
x
y
o
A
C
B
分析由
X-2y+1=0
y=0
A(-1,0)
kAB==-1
所以kAC=-1(为什么??)
因为x轴是A的平分线
AC:y=-(x+1)
KBC=-2
BC:y-2=-2(x-1)
C(5,-6)
例7:已知直线L过点P(3,2)且与x正半轴y正半轴分别交于 A、 B
(1)、求△AOB面积的最小值,及此时L的方程(O为原点)
(2)、求直线L在两轴上截距之和的最小值
例7:已知直线L过点P(3,2)且与x正半轴y正半轴分别交于 A、 B
(1)、求△AOB面积的最小值,及此时L的方程(O为原点)
(2)、求直线L在两轴上截距之和的最小值
练习3 、如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
课堂练习
O
x
y
A
C
B
解:
五、倾斜角、斜率、方向向量之间的关系
练习5 证明A(1,3),B(5,7),C(10,12)三点共线。
A,B,C三点共线
证明:
③设A,B的坐标分别是(x1,y1)和(x2,y2)且x1≠x2,
直线AB的斜率为k,求证:
㈣巩固:
⒈已知直线的倾斜角,求直线的斜率:①α=00 ②α=600
③α=900 ④α=3π/4
⒉已知直线的倾斜角的取值范围,利用正切函数的性质,讨
论直线斜率及其绝对值变化情况:①00<α<900 ②900<
α<1800
⒊求经过下列每两个点的直线的斜率和倾斜角:
①C(10,8),D(4,-4) ②P(0,0),Q(-1,√3)
③M(-√3,√2),N(-√2,√3)
练习:(1)求原点到直线 的距离;
(2)求点P(-1,2)到直线 的距离;
(3)求两条直线
的距离;
用点到直线的距离公式时直线方程要先化成一般式。
用两条平行直线间的距离公式时两个直线
方程x,y的系数化得一样。
一、直线的方程
k是直线的斜率,
b:直线在y轴上的截距
1、直线的斜截式方程
y=kx+b (k∈R)叫做直线的斜截式方程
直线过点(0,b)
x
y
o
已知直线l经过点P(x0,y0),并且与向量 平行,则直线l的方程
2、直线点方向式方程
x
y
o
3、直线的点法向式
已知直线l经过点P(x0,y0), 并且与向 量 垂直,求直线的方程
直线的点法向式方程
4、直线的一般式方程
5、直线的点斜式方程
6、直线的截距式方程
1、定义:①当直线l与x轴相交与M,我们将x轴绕着交点M按逆时针方向旋转到与l重合时所旋转的最小正角α叫做直线的倾斜角 。
2、范围: 0≤α<π。
3、任何一条直线都有倾斜角直线的倾斜角决定直线的方向。
②当直线l与x轴平行或重合时,规定直线的倾斜角 α=0
二、直线的倾斜角、斜率
4、已知倾斜角α,如何求直线斜率κ
5、已知直线斜率κ,如何求倾斜角α
α
k
o
三:直线的方向向量、法向量、斜率、倾斜角
法向量
方向向量
斜 率
倾斜角
坐标平面上的直线
第二课:
两直线的位置关系
相交
D≠0时,方程组有唯一解
X=Dx/D y=Dy/D
平行
D=0,Dx≠0或Dy≠0时方程组无解
重合
D=0,Dx=Dy=0时方程组有无数解
1、两直线的位置关系
设直线l1和l2的斜率为k1和k2,则“l1⊥l2 ”是
“k1·k2 =-1”充要条件
2、直线的平行
3、直线的垂直
设直线l1、l2的夹角为α,则
4、直线的夹角公式
O
x
y
点 到直线 的距离:
5、点到直线的距离
特殊地:
设点P(x,y),则
P到x轴的距离为
_______;
P到y轴的距离为
_______;
P到直线x-a=0的距离为
_______;
P到直线y-b=0的距离为
_______;
x
|y|
|x|
|x-a|
|y-b|
已知两条平行直线
l1:Ax+By+C1=0. l2:Ax+By+C2=0.
则两条平行直线的距离d为:
6、两条平行直线的距离
已知直线l:ax+by+c=0.点A(x1,y1)、B(x2,y2)则
(1)、A、B在直线同侧的充要条件为
(ax1+by1+c)· (ax2+by2+c)>0
(2)、A、B在直线异侧的充要条件为
(ax1+by1+c)· (ax2+by2+c)<0
(3)、直线与线段AB相交的充要条件为
(ax1+by1+c)· (ax2+by2+c)≤0
7、两直线与线段相交
课堂练习:(1)如果A(3, 1)、B(-2, k)、
C(8, 11),在同一直线上,那么k 的值是( )
(A)-6 (B)-7 (C)-8 (D)-9
(2)如果直线通过点(-1,-3), 并且与x轴平行,那么的方程是( )。
(A)y+3=0 (B)y-3=0
(C)x+1=0 (D)x-1=0
D
A
小结:证明三点共线的方法--斜率相等法,
直线方程法, 向量平行法, 线段相等法。
若将此题中的平行改为垂直,答案怎样?
练习2:
A、平行 B、重合 C、垂直 D相交但不垂直
C
、直线L过点A(2,3),且被两平行线L1:3x+4y-7=0和L2:3x+4y+8=0截得的线段长为 ,试求直线的方程
练习3:
练习4、一直线被两直线L1:4x+y+6=0,L2:3x-5y-6=0截得的线段的中点恰好是坐标原点,求该直线方程
5、在三角形ABC中,BC边上的高所在直线的方程为x-2y+1=0,A的平分线所在直线的方程为y=0,若B点的坐标为(1,2),求点A和点C的坐标
6、已知三角形ABC的一条内角平分线CD的方程是2x+y-1=0,两个顶点A(1,2) B(-1,-1),求第三个顶点C的坐标
x
y
o
A
C
B
分析由
X-2y+1=0
y=0
A(-1,0)
kAB==-1
所以kAC=-1(为什么??)
因为x轴是A的平分线
AC:y=-(x+1)
KBC=-2
BC:y-2=-2(x-1)
C(5,-6)
例7:已知直线L过点P(3,2)且与x正半轴y正半轴分别交于 A、 B
(1)、求△AOB面积的最小值,及此时L的方程(O为原点)
(2)、求直线L在两轴上截距之和的最小值
例7:已知直线L过点P(3,2)且与x正半轴y正半轴分别交于 A、 B
(1)、求△AOB面积的最小值,及此时L的方程(O为原点)
(2)、求直线L在两轴上截距之和的最小值
练习3 、如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
课堂练习
O
x
y
A
C
B
解:
五、倾斜角、斜率、方向向量之间的关系
练习5 证明A(1,3),B(5,7),C(10,12)三点共线。
A,B,C三点共线
证明:
③设A,B的坐标分别是(x1,y1)和(x2,y2)且x1≠x2,
直线AB的斜率为k,求证:
㈣巩固:
⒈已知直线的倾斜角,求直线的斜率:①α=00 ②α=600
③α=900 ④α=3π/4
⒉已知直线的倾斜角的取值范围,利用正切函数的性质,讨
论直线斜率及其绝对值变化情况:①00<α<900 ②900<
α<1800
⒊求经过下列每两个点的直线的斜率和倾斜角:
①C(10,8),D(4,-4) ②P(0,0),Q(-1,√3)
③M(-√3,√2),N(-√2,√3)
练习:(1)求原点到直线 的距离;
(2)求点P(-1,2)到直线 的距离;
(3)求两条直线
的距离;
用点到直线的距离公式时直线方程要先化成一般式。
用两条平行直线间的距离公式时两个直线
方程x,y的系数化得一样。
