人教A版(2019)高中数学必修第一册 4.3.1 对数的概念 课件(20张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第一册 4.3.1 对数的概念 课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 20:55:05 | ||
图片预览








文档简介
4.3.1 对数的概念
第四章 指数函数与对数函数
问题:请计算下面的式子(不使用计算器):
问题的引入
?
问题的引入
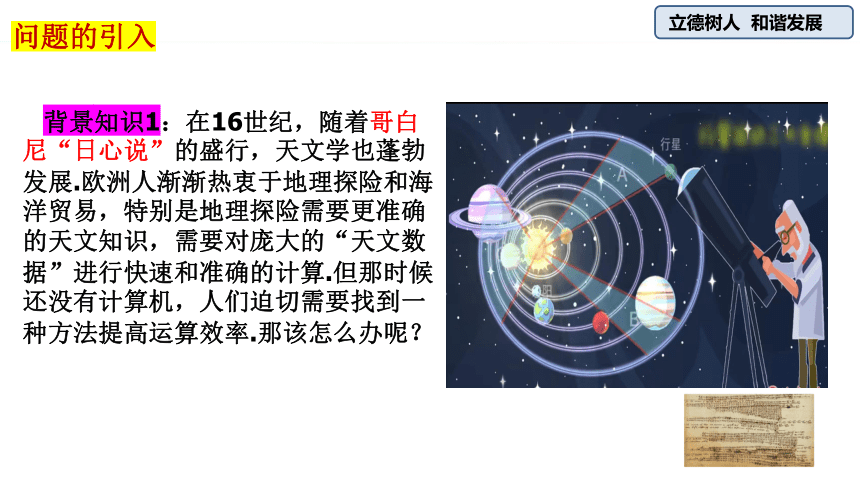
背景知识1:在16世纪,随着哥白尼“日心说”的盛行,天文学也蓬勃发展.欧洲人渐渐热衷于地理探险和海洋贸易,特别是地理探险需要更准确的天文知识,需要对庞大的“天文数据”进行快速和准确的计算.但那时候还没有计算机,人们迫切需要找到一种方法提高运算效率.那该怎么办呢?
问题:请计算下面的式子(不使用计算器):
问题的引入
?
探究发现
问题:请计算下面的式子(不使用计算器):
?
1544年,德国数学家斯蒂菲尔研究了下面的两行数:
探究发现
?
背景知识2:苏格兰数学家纳皮尔就花了20多年的时间编制出这样的表格,不过他选取的底数不是2,而是一个较复杂的数.后来英国数学家布里格斯专程拜访了纳皮尔,建议将底数改为10,符合人们使用十进制的习惯.于是,他花了大量时间和精力,终于在1617年编制了以10为底的表格,以供人们计算较大的数据.
形成概念
生活中的例子:
截止到1999年底我国有13亿人口,如果今后我们能将人口年平均增长率控制在1%,问我国哪一年的人口数可以达到20亿?
?
?
这是已知底数和幂的值,求指数!应怎样来求呢?
形成概念
logarithm
对数的概念
形成概念
常用对数:
自然对数:
形成概念
背景知识3 :对数是指数的逆运算.但有趣的是,在数学史上,对数却是先于指数被发现的.1614年,纳皮尔发明了对数和对数表.1637年,法国数学家笛卡儿发明了指数,比对数晚了20多年,当时人们并没有发现指数和对数之间的关系.后来,数学家欧拉才提出“对数源于指数”,这一说法得到了数学家们的广泛认可.至此,对数逐渐得到完善,成为我们今天所用的对数.
伽利略
拉普拉斯
形成概念
底数
幂
真数
指数
对数
指数式和对数式的关系相互转化
概念深化
概念深化
把下列指数式化为对数式,对数式化为指数式
概念深化
⑴负数与零没有对数
⑶对数恒等式
概念深化
巩固应用
巩固应用
巩固应用
(1)对数的由来
(2)对数的定义
(3)常用对数与自然对数
课堂小结
作业布置
第四章 指数函数与对数函数
问题:请计算下面的式子(不使用计算器):
问题的引入
?
问题的引入
背景知识1:在16世纪,随着哥白尼“日心说”的盛行,天文学也蓬勃发展.欧洲人渐渐热衷于地理探险和海洋贸易,特别是地理探险需要更准确的天文知识,需要对庞大的“天文数据”进行快速和准确的计算.但那时候还没有计算机,人们迫切需要找到一种方法提高运算效率.那该怎么办呢?
问题:请计算下面的式子(不使用计算器):
问题的引入
?
探究发现
问题:请计算下面的式子(不使用计算器):
?
1544年,德国数学家斯蒂菲尔研究了下面的两行数:
探究发现
?
背景知识2:苏格兰数学家纳皮尔就花了20多年的时间编制出这样的表格,不过他选取的底数不是2,而是一个较复杂的数.后来英国数学家布里格斯专程拜访了纳皮尔,建议将底数改为10,符合人们使用十进制的习惯.于是,他花了大量时间和精力,终于在1617年编制了以10为底的表格,以供人们计算较大的数据.
形成概念
生活中的例子:
截止到1999年底我国有13亿人口,如果今后我们能将人口年平均增长率控制在1%,问我国哪一年的人口数可以达到20亿?
?
?
这是已知底数和幂的值,求指数!应怎样来求呢?
形成概念
logarithm
对数的概念
形成概念
常用对数:
自然对数:
形成概念
背景知识3 :对数是指数的逆运算.但有趣的是,在数学史上,对数却是先于指数被发现的.1614年,纳皮尔发明了对数和对数表.1637年,法国数学家笛卡儿发明了指数,比对数晚了20多年,当时人们并没有发现指数和对数之间的关系.后来,数学家欧拉才提出“对数源于指数”,这一说法得到了数学家们的广泛认可.至此,对数逐渐得到完善,成为我们今天所用的对数.
伽利略
拉普拉斯
形成概念
底数
幂
真数
指数
对数
指数式和对数式的关系相互转化
概念深化
概念深化
把下列指数式化为对数式,对数式化为指数式
概念深化
⑴负数与零没有对数
⑶对数恒等式
概念深化
巩固应用
巩固应用
巩固应用
(1)对数的由来
(2)对数的定义
(3)常用对数与自然对数
课堂小结
作业布置
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
