人教A版高中数学必修四2.4.1《平面向量数量积的物理背景及其含义》教学课件(21张PPT)
文档属性
| 名称 | 人教A版高中数学必修四2.4.1《平面向量数量积的物理背景及其含义》教学课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览




文档简介
(1)理解和掌握向量数量积的定义;
(2)掌握向量数量积的重要性质;
(3)理解向量数量积的几何意义;
(4)掌握向量数量积的运算律
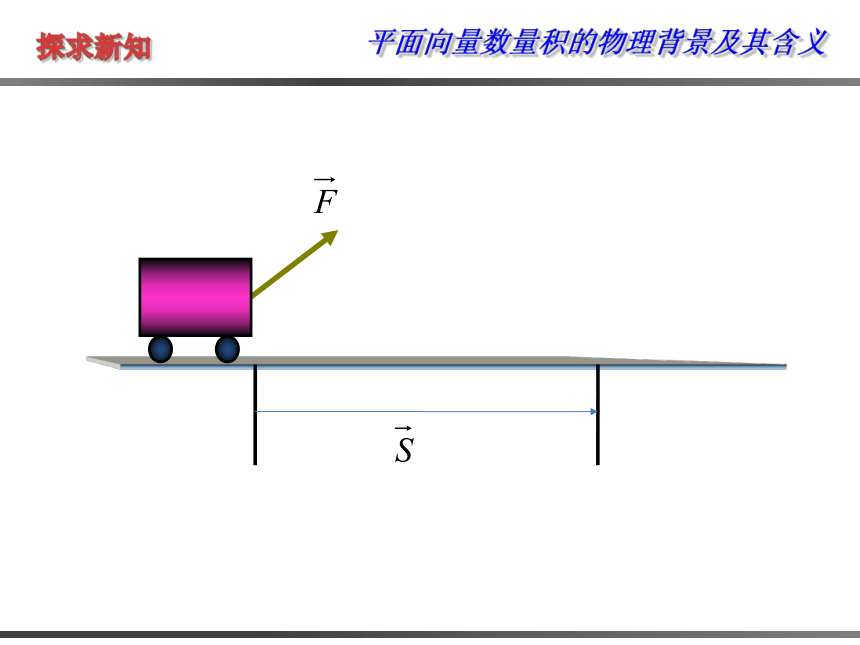
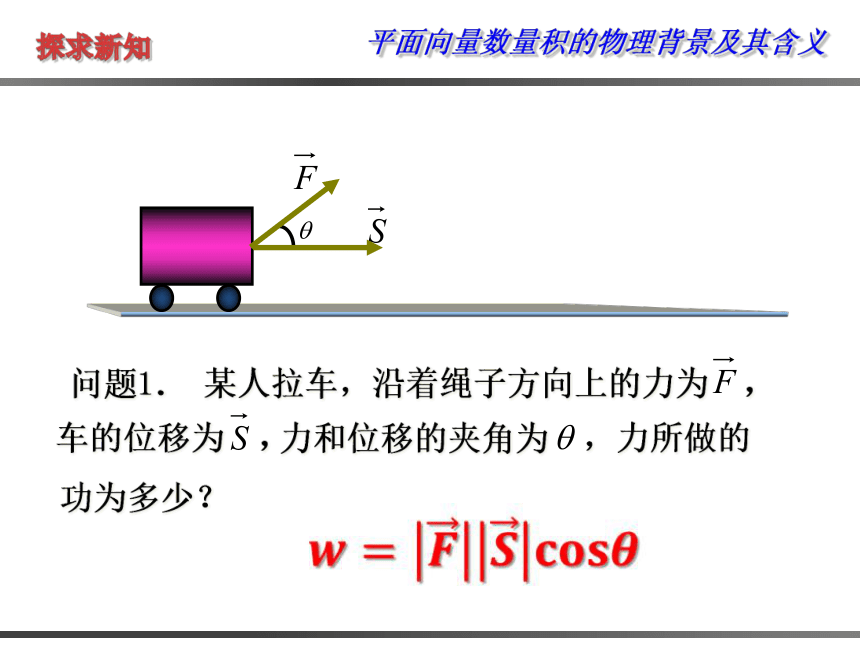
问题1. 某人拉车,沿着绳子方向上的力为 ,
车的位移为 ,
力和位移的夹角为 ,力所做的
功为多少?
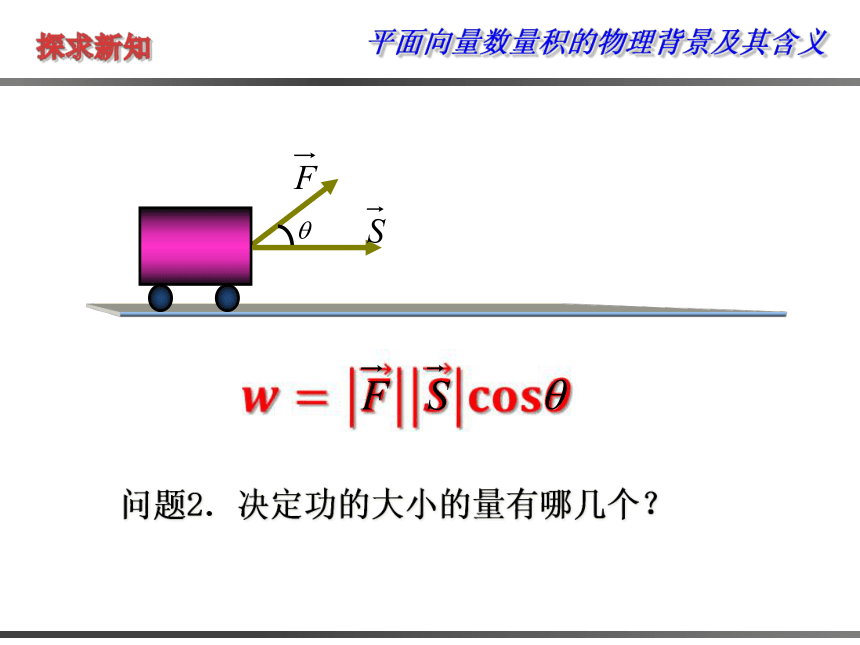
问题2.决定功的大小的量有哪几个?
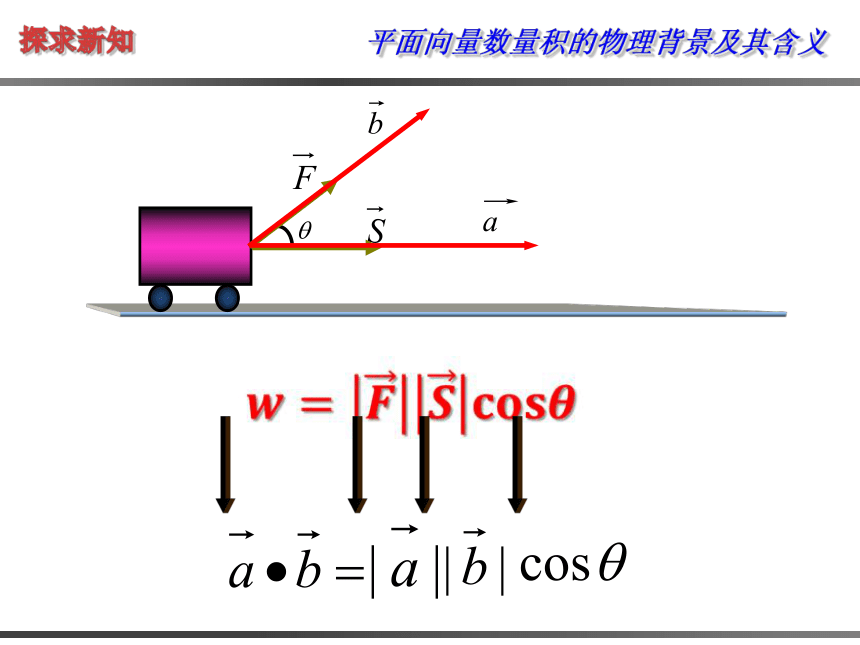
定义 已知两个非零向量 与 ,我们把数量
叫做向量 与 的数量积(或内积),记作 ,即 ,
其中 是 与 的夹角.
规定:零向量与任一向量的数量积为0.
问题3.决定向量数量积的大小的量有哪几个?
数量积的正、负、零由谁决定?
A
C
B
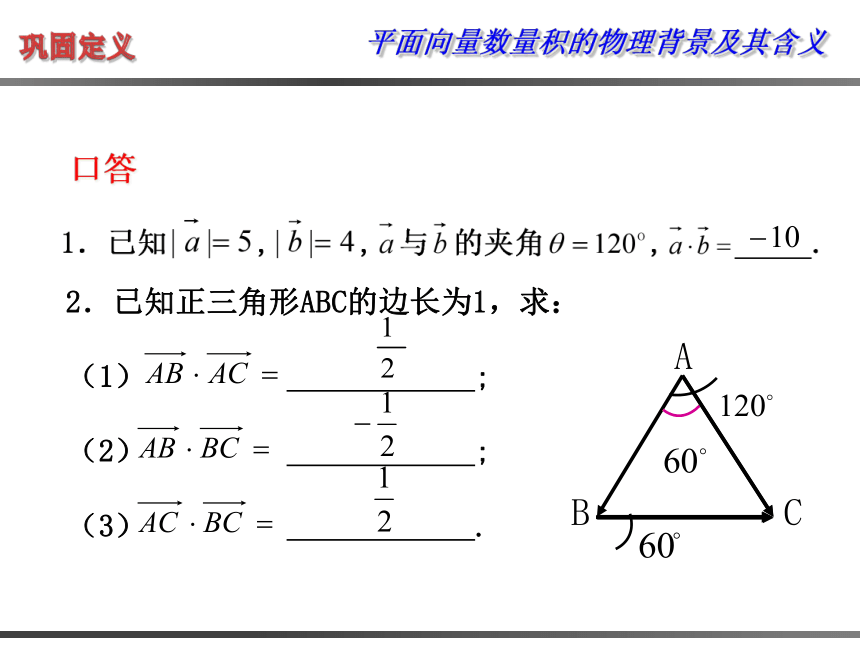
2.已知正三角形ABC的边长为1,求:
(1) ;
(2) ;
(3) .
口答
(1) ;
(2)若 与 同向,则 ;
若 与 反向,则 ;
特别地, ,
3.依据数量积定义完成以下问题( 与 是非零向量)
(4) .
≤
(3)
;
判定两向量垂直
用于计算向量的模
用于计算向量的夹角,以
及判断三角形的形状.
平面向量数量积的性质 ( 与 是非零向量)
B
B1
叫做 在 方向上的投影;
叫做 在 方向上的投影;
平面向量数量积的几何意义
数量积 等于 的长度 与 在 上的投
影 的乘积.
探究:数量积作为一种运算,有怎样的运算律呢?
实数乘法
交换律
结合律
分配律
向量的数量积
运算律
平面向量数量积的运算律
交换律
结合律
分配律
(a + b) ·c = ON |c|
= (OM + MN) |c|
= OM|c| + MN|c|
= a·c + b·c .
O
N
M
a+b
b
a
c
向量a、b、a + b在c上的射影的数量分别是OM、MN、 ON, 则
证明分配律:
1.若a=0,则对任一向量b ,有a · b=0
2.若a≠0,则对任一非零向量b,有a · b≠0
3.若a≠0,a · b=0,则b=0
4.若a · b=0,则a · b中至少有一个为0
5.若b≠0,a · b= b · c,则a=c
6.若a · b= a · c ,则b≠c,当且仅当a=0时成立
7对任一向量a,有a2=|a|2
练习:判断正误
( √ )
( × )
( × )
( × )
( × )
( × )
( √ )
例1.证明(1) ;
(2) .
证明:(1)
(2)
例2.已知 , , 与 的夹角为 ,
求 .
解:
例3 已知︱ ︱=3,︱ ︱=4,且 与 不共线.求
当k为何值时,向量 +k 与 -k 互相垂直?
1.在△ABC中, =a , =b ,a·b<0 ,则△ABC
是_____三角形
BA
BC
2.已知 |a| =4,е为单位向量,它们的夹角为
则 a在е方向上的投影是_____
2π
3
3.设a、b、c是非零向量,则(a·b)·c是( )
(A)数量
(B)与a共线的向量
(C) 与c共线的向量
(D)无意义
钝角
–2
C
今天你学到了什么?
(2)掌握向量数量积的重要性质;
(3)理解向量数量积的几何意义;
(4)掌握向量数量积的运算律
问题1. 某人拉车,沿着绳子方向上的力为 ,
车的位移为 ,
力和位移的夹角为 ,力所做的
功为多少?
问题2.决定功的大小的量有哪几个?
定义 已知两个非零向量 与 ,我们把数量
叫做向量 与 的数量积(或内积),记作 ,即 ,
其中 是 与 的夹角.
规定:零向量与任一向量的数量积为0.
问题3.决定向量数量积的大小的量有哪几个?
数量积的正、负、零由谁决定?
A
C
B
2.已知正三角形ABC的边长为1,求:
(1) ;
(2) ;
(3) .
口答
(1) ;
(2)若 与 同向,则 ;
若 与 反向,则 ;
特别地, ,
3.依据数量积定义完成以下问题( 与 是非零向量)
(4) .
≤
(3)
;
判定两向量垂直
用于计算向量的模
用于计算向量的夹角,以
及判断三角形的形状.
平面向量数量积的性质 ( 与 是非零向量)
B
B1
叫做 在 方向上的投影;
叫做 在 方向上的投影;
平面向量数量积的几何意义
数量积 等于 的长度 与 在 上的投
影 的乘积.
探究:数量积作为一种运算,有怎样的运算律呢?
实数乘法
交换律
结合律
分配律
向量的数量积
运算律
平面向量数量积的运算律
交换律
结合律
分配律
(a + b) ·c = ON |c|
= (OM + MN) |c|
= OM|c| + MN|c|
= a·c + b·c .
O
N
M
a+b
b
a
c
向量a、b、a + b在c上的射影的数量分别是OM、MN、 ON, 则
证明分配律:
1.若a=0,则对任一向量b ,有a · b=0
2.若a≠0,则对任一非零向量b,有a · b≠0
3.若a≠0,a · b=0,则b=0
4.若a · b=0,则a · b中至少有一个为0
5.若b≠0,a · b= b · c,则a=c
6.若a · b= a · c ,则b≠c,当且仅当a=0时成立
7对任一向量a,有a2=|a|2
练习:判断正误
( √ )
( × )
( × )
( × )
( × )
( × )
( √ )
例1.证明(1) ;
(2) .
证明:(1)
(2)
例2.已知 , , 与 的夹角为 ,
求 .
解:
例3 已知︱ ︱=3,︱ ︱=4,且 与 不共线.求
当k为何值时,向量 +k 与 -k 互相垂直?
1.在△ABC中, =a , =b ,a·b<0 ,则△ABC
是_____三角形
BA
BC
2.已知 |a| =4,е为单位向量,它们的夹角为
则 a在е方向上的投影是_____
2π
3
3.设a、b、c是非零向量,则(a·b)·c是( )
(A)数量
(B)与a共线的向量
(C) 与c共线的向量
(D)无意义
钝角
–2
C
今天你学到了什么?
