人教A版高中数学选修2-1 2.4抛物线及其标准方程课件(30张PPT)
文档属性
| 名称 | 人教A版高中数学选修2-1 2.4抛物线及其标准方程课件(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:05:51 | ||
图片预览










文档简介
人教A版高中数学选修2-1 高二年级
抛物线的生活实例
夜色下的喷泉
抛物线的生活实例
1.掌握抛物线的定义及标准方程.(重点)
2.能求简单抛物线的方程.(重点、难点)
M
·
F
·
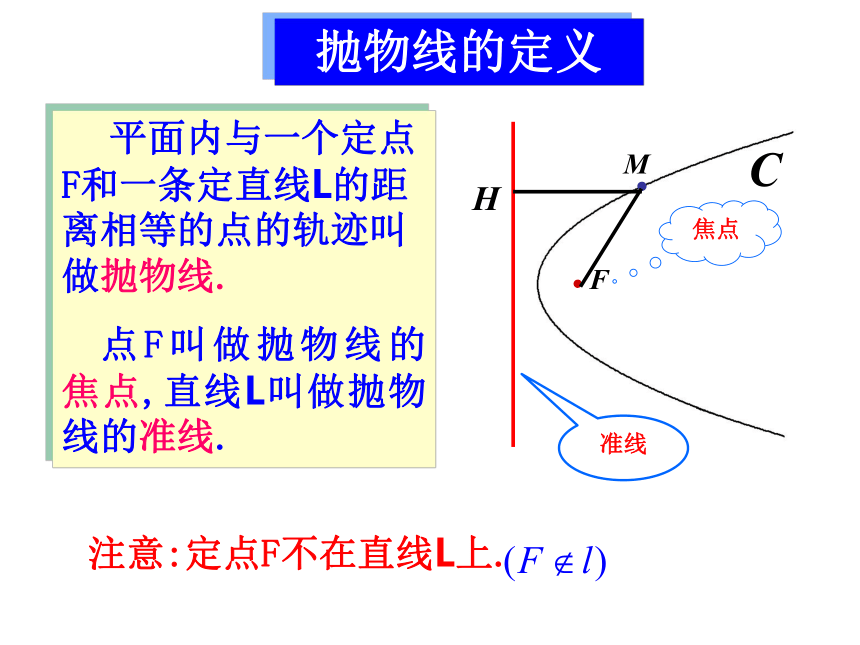
抛物线的定义
平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,直线L叫做抛物线的准线.
注意:定点F不在直线L上.
焦点
准线
明确了抛物线的定义,
你能根据定义求出抛物线的方程吗?
一条经过点F且垂直于l 的直线
想一想:
定义中当直线l 经过定点F,则点M的轨迹是什么?
l
·
F
·
·
·
·
·
·
类比椭圆、双曲线标准方程的建立过程,你认为如何选择坐标系,求抛物线的方程?
思考
L
F
K
M
N
(1)
L
F
K
M
N
L
F
K
M
N
(3)
(2)
化 简
列 式
设 点
建 系
以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.
x
K
y
O
F
M
l
·
·
·
(x,y)
设M(x,y)是抛物线上任意一点,
H
点M到l的距离为d.
d
由抛物线的定义,抛物线就是点的集合
探究点2 抛物线的标准方程
(p>0),
两边平方,整理得
x
K
y
O
F
M
l
·
·
·
(x, y)
H
d
方程
叫做抛物线的标准方程.
它表示的抛物线焦点在x轴的正半轴上,焦点坐标是 ,它的准线方程是 。
其中p为正常数,它的几何意义是:
抛物线的标准方程
L
F
K
M
N
焦点到准线的距离。
准线方程
焦点坐标
标准方程
图
形
y2=2px
y2=-2px
x2=2py
x2=-2py
F(-
-
-
-
如何由抛物线的标准方程确定焦点位置和开口方向?
一次定焦点,正负定方向
例1(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。
解:因为p=3,故焦点坐标为(-,0)
准线方程为x=- -.
32
32
1
12
解:方程可化为:x =- -y,故p=-,焦点坐标
为(0, --),准线方程为y= -.
16
1 24
1 24
2
解:因焦点在y轴的负半轴上,且p=4,故其标准方程为:x = - 8y
2
1、求下列抛物线的焦点坐标和准线方程:
焦点坐标
准线方程
(1)
(2)
(3)
(4)
注意:
求抛物线的焦点一定要先把抛物线方程化为标准形式。
课堂练习
课堂练习
2、根据下列条件,写出抛物线的标准方程:
(3)焦点到准线的距离是2.
(1)焦点是 ;
(2)准线方程是 ;
或
小结:已知抛物线的标准方程
求其焦点坐标和准线方程.
先定位,后定量
课堂练习
3、设抛物线 上一点P到y轴的距离是4,
则点P到该抛物线焦点的距离是( )
A.4 B.6 C.8 D.12
B
例2.求过点A(-3,2)的抛物线的标准方程.
.
A
O
y
x
解:(1)当抛物线的焦点在 y 轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p=
(2)当焦点在 x 轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y 或y2 = x 。
抛物线方程
左右型
标准方程为
y2 =+ 2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
上下型
怎样把抛物线的位置特征(标准位置)
和方程特征(标准方程)统一起来?
想一想?
思考题 M是抛物线y2 = 2px(P>0)上一点,
若点M 的横坐标为X0,则点M到焦点的距离是
———————————
X0 + —
2
p
O
y
x
.
F
M
.
课后作业
1.巩固作业:学案P41-42
2.探究作业:为什么二次函数的图象是抛物线
4.标准方程中p前面的正负号决定抛物线的
开口方向.
1.抛物线的定义;
2.抛物线的标准方程有四种不同的形式,
每一对焦点和准线对应一种形式;
3.P 的几何意义是:
焦点到准线的距离;
课堂小结
小 结 :
1、抛物线的定义,标准方程类型与图象
的对应关系以及判断方法
2、抛物线的定义、标准方程和它的
焦点、准线、方程
3、求标准方程
(1)用定义;
(2)用待定系数法.
*
1.抛物线的定义;
2.抛物线的标准方程;
顶
点
在
原
点
对称轴
为x轴
对称轴
为y轴
标准方程为
y2= 2px(p>0)
标准方程为
x2= 2py(p>0)
开口与x轴正向同向:y2=2px
开口与x轴正向反向:y2=-2px
开口与y轴正向同向:x2=2py
开口与y轴正向反向:x2=-2py
+
+
3.
已知抛物线的标准方程求焦点坐标和准线方程时,
应先“定位”;后“定量”.
课堂小结
课后思考
1.M是抛物线y2 = 2px(p>0)上一点,
若点M 的横坐标为x0,则点M到焦点的距离是——
2.
为什么二次函数的图像是抛物线?
O
y
x
.
F
M
.
抛物线的生活实例
夜色下的喷泉
抛物线的生活实例
1.掌握抛物线的定义及标准方程.(重点)
2.能求简单抛物线的方程.(重点、难点)
M
·
F
·
抛物线的定义
平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,直线L叫做抛物线的准线.
注意:定点F不在直线L上.
焦点
准线
明确了抛物线的定义,
你能根据定义求出抛物线的方程吗?
一条经过点F且垂直于l 的直线
想一想:
定义中当直线l 经过定点F,则点M的轨迹是什么?
l
·
F
·
·
·
·
·
·
类比椭圆、双曲线标准方程的建立过程,你认为如何选择坐标系,求抛物线的方程?
思考
L
F
K
M
N
(1)
L
F
K
M
N
L
F
K
M
N
(3)
(2)
化 简
列 式
设 点
建 系
以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.
x
K
y
O
F
M
l
·
·
·
(x,y)
设M(x,y)是抛物线上任意一点,
H
点M到l的距离为d.
d
由抛物线的定义,抛物线就是点的集合
探究点2 抛物线的标准方程
(p>0),
两边平方,整理得
x
K
y
O
F
M
l
·
·
·
(x, y)
H
d
方程
叫做抛物线的标准方程.
它表示的抛物线焦点在x轴的正半轴上,焦点坐标是 ,它的准线方程是 。
其中p为正常数,它的几何意义是:
抛物线的标准方程
L
F
K
M
N
焦点到准线的距离。
准线方程
焦点坐标
标准方程
图
形
y2=2px
y2=-2px
x2=2py
x2=-2py
F(-
-
-
-
如何由抛物线的标准方程确定焦点位置和开口方向?
一次定焦点,正负定方向
例1(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。
解:因为p=3,故焦点坐标为(-,0)
准线方程为x=- -.
32
32
1
12
解:方程可化为:x =- -y,故p=-,焦点坐标
为(0, --),准线方程为y= -.
16
1 24
1 24
2
解:因焦点在y轴的负半轴上,且p=4,故其标准方程为:x = - 8y
2
1、求下列抛物线的焦点坐标和准线方程:
焦点坐标
准线方程
(1)
(2)
(3)
(4)
注意:
求抛物线的焦点一定要先把抛物线方程化为标准形式。
课堂练习
课堂练习
2、根据下列条件,写出抛物线的标准方程:
(3)焦点到准线的距离是2.
(1)焦点是 ;
(2)准线方程是 ;
或
小结:已知抛物线的标准方程
求其焦点坐标和准线方程.
先定位,后定量
课堂练习
3、设抛物线 上一点P到y轴的距离是4,
则点P到该抛物线焦点的距离是( )
A.4 B.6 C.8 D.12
B
例2.求过点A(-3,2)的抛物线的标准方程.
.
A
O
y
x
解:(1)当抛物线的焦点在 y 轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p=
(2)当焦点在 x 轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y 或y2 = x 。
抛物线方程
左右型
标准方程为
y2 =+ 2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
上下型
怎样把抛物线的位置特征(标准位置)
和方程特征(标准方程)统一起来?
想一想?
思考题 M是抛物线y2 = 2px(P>0)上一点,
若点M 的横坐标为X0,则点M到焦点的距离是
———————————
X0 + —
2
p
O
y
x
.
F
M
.
课后作业
1.巩固作业:学案P41-42
2.探究作业:为什么二次函数的图象是抛物线
4.标准方程中p前面的正负号决定抛物线的
开口方向.
1.抛物线的定义;
2.抛物线的标准方程有四种不同的形式,
每一对焦点和准线对应一种形式;
3.P 的几何意义是:
焦点到准线的距离;
课堂小结
小 结 :
1、抛物线的定义,标准方程类型与图象
的对应关系以及判断方法
2、抛物线的定义、标准方程和它的
焦点、准线、方程
3、求标准方程
(1)用定义;
(2)用待定系数法.
*
1.抛物线的定义;
2.抛物线的标准方程;
顶
点
在
原
点
对称轴
为x轴
对称轴
为y轴
标准方程为
y2= 2px(p>0)
标准方程为
x2= 2py(p>0)
开口与x轴正向同向:y2=2px
开口与x轴正向反向:y2=-2px
开口与y轴正向同向:x2=2py
开口与y轴正向反向:x2=-2py
+
+
3.
已知抛物线的标准方程求焦点坐标和准线方程时,
应先“定位”;后“定量”.
课堂小结
课后思考
1.M是抛物线y2 = 2px(p>0)上一点,
若点M 的横坐标为x0,则点M到焦点的距离是——
2.
为什么二次函数的图像是抛物线?
O
y
x
.
F
M
.
