人教A版数学必修五1.1.1 正弦定理 同步教学课件(23张PPT)
文档属性
| 名称 | 人教A版数学必修五1.1.1 正弦定理 同步教学课件(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览





文档简介
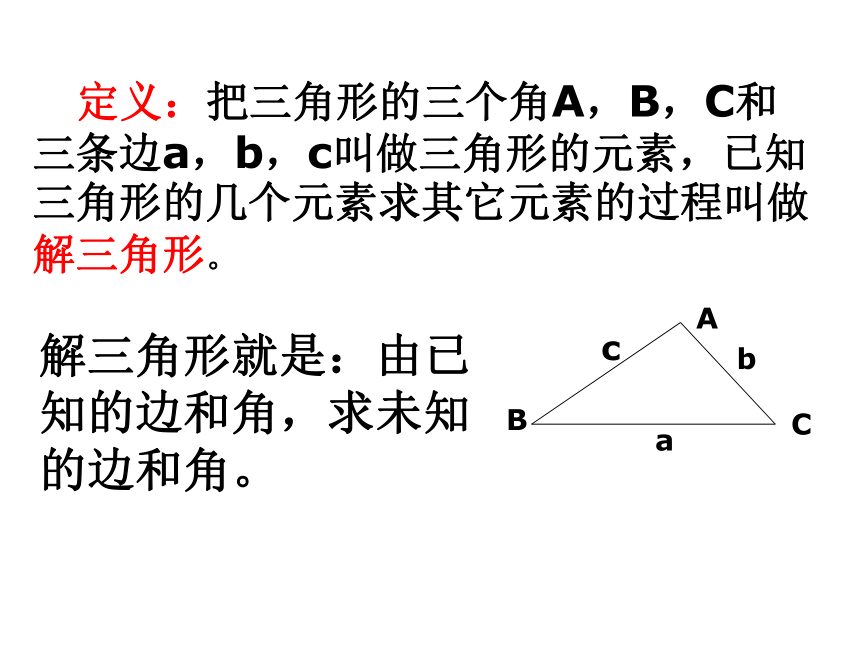
定义:把三角形的三个角A,B,C和三条边a,b,c叫做三角形的元素,已知三角形的几个元素求其它元素的过程叫做解三角形。
A
B
C
a
b
c
解三角形就是:由已知的边和角,求未知的边和角。
请你回顾一下:同一三角形中的边角关系
知识回顾:
a+b>c, a+c>b, b+c>a
(1)三边:
(2)三角:
(3)边角:
大边对大角
A
B
C
a
b
c
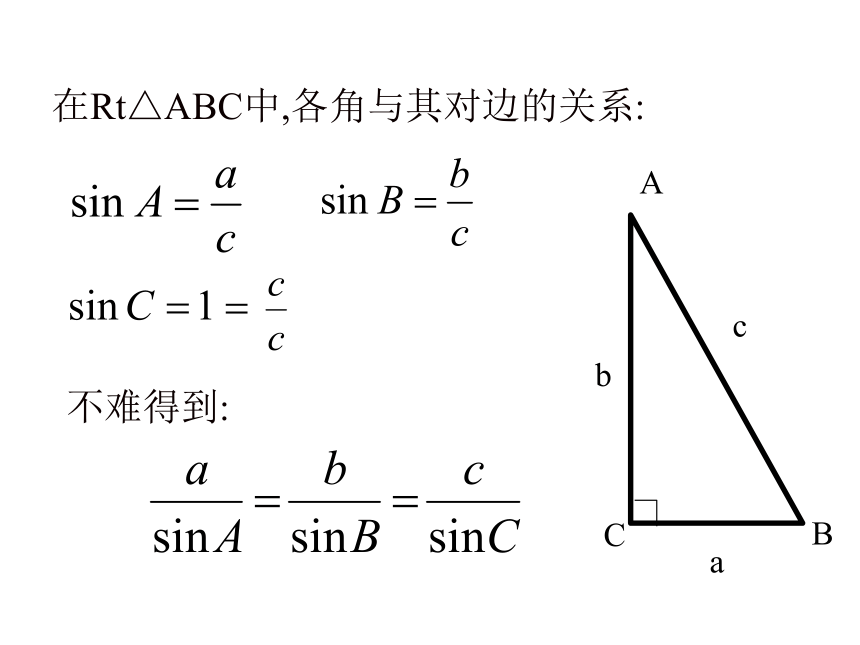
在Rt△ABC中,各角与其对边的关系:
不难得到:
C
B
A
a
b
c
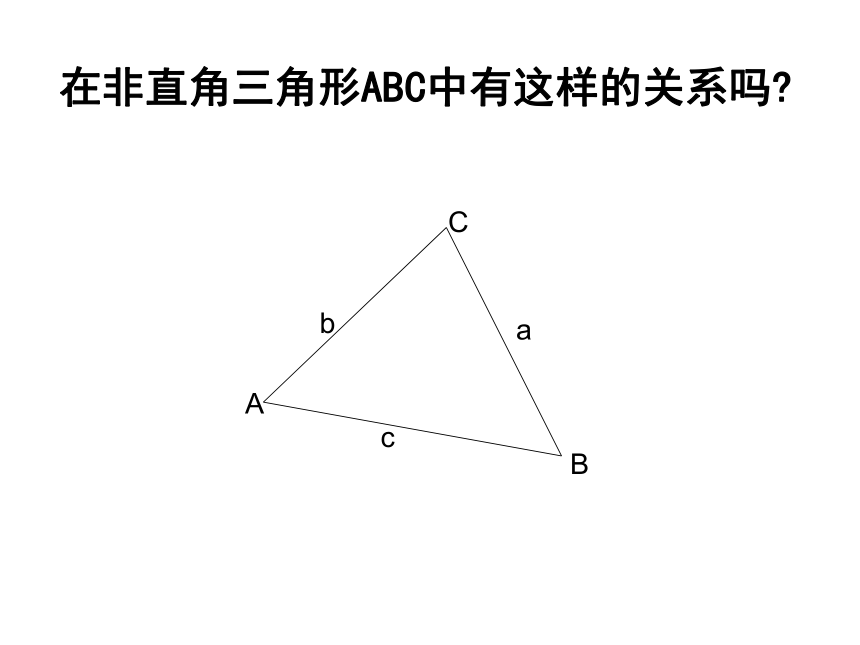
在非直角三角形ABC中有这样的关系吗?
A
c
b
a
C
B
(1) 若直角三角形,已得结论成立.
所以AD=csinB=bsinC, 即
同理可得
D
A
c
b
C
B
图1
过点A作AD⊥BC于D,
此时有
(2)若三角形是锐角三角形, 如图1,
且
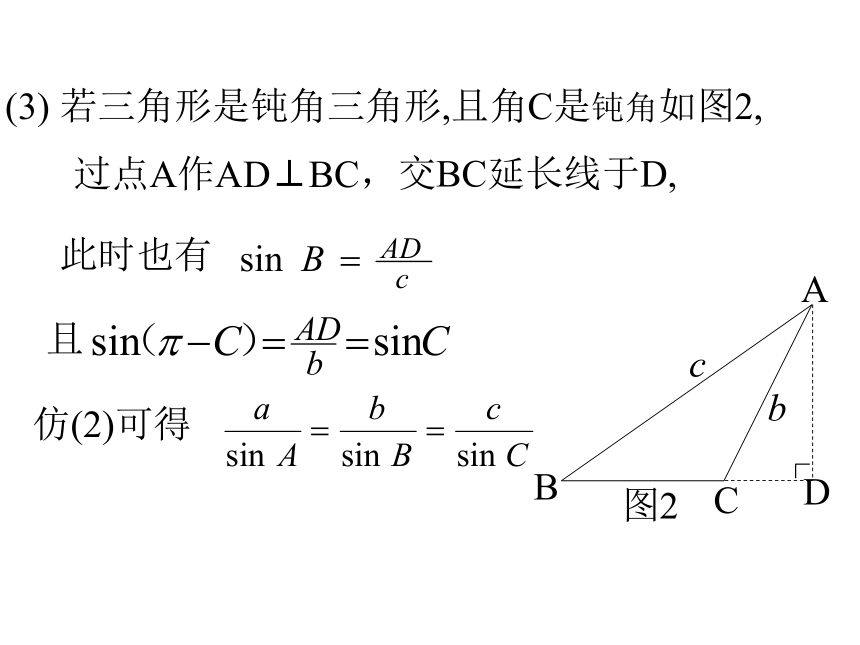
仿(2)可得
D
(3) 若三角形是钝角三角形,且角C是钝角如图2,
此时也有
交BC延长线于D,
过点A作AD⊥BC,
C
A
c
b
B
图2
(1)文字叙述
正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.
(2)结构特点
和谐美、对称美.
正弦定理:
证明:
O
C/
c
b
a
C
B
A
作外接圆O,
过B作直径BC/,连AC/,
=
=
(2R为△ABC外接圆直径)
=
2R
在一个三角形中各边和它所对角的正弦的
比相等.
正弦定理的应用:解三角形
(边化角)
(角化边)
在 中,角A,B,C的对边分别是a,b,c,且
解三角形。
解:由正弦定理 得:
正弦定理应用一:
已知两角和任意一边,求其余两边和一角
例 1:
1、在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b.
解:
且
∵
∴
b =
=
∵
∴
a =
=
B
A
C
b
c
a
练习
例 2
已知a=16, b= , A=30° .
求角B,C和边c
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
当B=120°时
C=180°-A-B=30°
C=180°-A-B=90°
正弦定理应用二:已知两边及其一边的对角
例 2
已知a=16, b= , A=30° .
求角B,C和边c
已知两边和其中一边
的对角,求其他边和角
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
C=180°-A-B=90°
C=180°-A-B=30°
当B=120°时
300
A
B
C
16
3
16
∵ b > a ∴ B > A ,
C=180°-A-B=90°
16
B
三角形中大边对大角
所以
B=300,
或B=1500
由于1500 +450>1800
故B只有一解 (如图)
C=1050,
变式: a=4, b= , A=45°求角B,C和边c
解:由正弦定理
得
450
A
B
C
4
三角形中大边对大角
变式: a=4, b= , A=45°求角B,C和边c
解:由正弦定理
得
所以
B=300,
C=1050,
∵a > b ∴ A > B ,
三角形中大边对大角
450
A
B
C
4
在 中,已知 解三角形.
解:由正弦定理,得
故此三角形无解。
(边化角)
(角化边)
正弦定理:
定理变式:
(边化角)
(角化边)
1、在 中,已知
解三角形.
2、在 中,已知
解三角形.
A
B
C
a
b
c
解三角形就是:由已知的边和角,求未知的边和角。
请你回顾一下:同一三角形中的边角关系
知识回顾:
a+b>c, a+c>b, b+c>a
(1)三边:
(2)三角:
(3)边角:
大边对大角
A
B
C
a
b
c
在Rt△ABC中,各角与其对边的关系:
不难得到:
C
B
A
a
b
c
在非直角三角形ABC中有这样的关系吗?
A
c
b
a
C
B
(1) 若直角三角形,已得结论成立.
所以AD=csinB=bsinC, 即
同理可得
D
A
c
b
C
B
图1
过点A作AD⊥BC于D,
此时有
(2)若三角形是锐角三角形, 如图1,
且
仿(2)可得
D
(3) 若三角形是钝角三角形,且角C是钝角如图2,
此时也有
交BC延长线于D,
过点A作AD⊥BC,
C
A
c
b
B
图2
(1)文字叙述
正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.
(2)结构特点
和谐美、对称美.
正弦定理:
证明:
O
C/
c
b
a
C
B
A
作外接圆O,
过B作直径BC/,连AC/,
=
=
(2R为△ABC外接圆直径)
=
2R
在一个三角形中各边和它所对角的正弦的
比相等.
正弦定理的应用:解三角形
(边化角)
(角化边)
在 中,角A,B,C的对边分别是a,b,c,且
解三角形。
解:由正弦定理 得:
正弦定理应用一:
已知两角和任意一边,求其余两边和一角
例 1:
1、在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b.
解:
且
∵
∴
b =
=
∵
∴
a =
=
B
A
C
b
c
a
练习
例 2
已知a=16, b= , A=30° .
求角B,C和边c
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
当B=120°时
C=180°-A-B=30°
C=180°-A-B=90°
正弦定理应用二:已知两边及其一边的对角
例 2
已知a=16, b= , A=30° .
求角B,C和边c
已知两边和其中一边
的对角,求其他边和角
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
C=180°-A-B=90°
C=180°-A-B=30°
当B=120°时
300
A
B
C
16
3
16
∵ b > a ∴ B > A ,
C=180°-A-B=90°
16
B
三角形中大边对大角
所以
B=300,
或B=1500
由于1500 +450>1800
故B只有一解 (如图)
C=1050,
变式: a=4, b= , A=45°求角B,C和边c
解:由正弦定理
得
450
A
B
C
4
三角形中大边对大角
变式: a=4, b= , A=45°求角B,C和边c
解:由正弦定理
得
所以
B=300,
C=1050,
∵a > b ∴ A > B ,
三角形中大边对大角
450
A
B
C
4
在 中,已知 解三角形.
解:由正弦定理,得
故此三角形无解。
(边化角)
(角化边)
正弦定理:
定理变式:
(边化角)
(角化边)
1、在 中,已知
解三角形.
2、在 中,已知
解三角形.
