人教版数学七年级上册:4.3.3 余角和补角 同步练习(Word版 附答案)
文档属性
| 名称 | 人教版数学七年级上册:4.3.3 余角和补角 同步练习(Word版 附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 40.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 23:36:05 | ||
图片预览

文档简介
4.3.3 余角和补角
1.如果α与β互为余角,那么( )
A.α+β=180° B.α-β=180°
C.α-β=90° D.α+β=90°
2.已知∠A=55°,则它的余角是( )
A.25° B.35°
C.45° D.55°
3.如图,直线a与直线c相交于点O,∠1的余角的度数是( )
A.60° B.50°
C.40° D.30°
4.若∠α=35°,则∠α的补角为 .
5.一个角是70°39′,则它的余角的度数是 .
6.(1)已知一个角是它的余角的一半,求这个角的度数;
(2)如图,∠AOB=114°,OD是∠AOB的平分线,∠1与∠2互余,求∠1的度数.
7.已知∠1+∠2=180°,∠3+∠4=180°,如果∠1=∠3,那么∠2=∠4,依据是( )
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等 D.等角的补角相等
8.已知∠A与∠B互余,∠B与∠C互余,则∠A与∠C( )
A.互余 B.相等
C.互补 D.差为90°
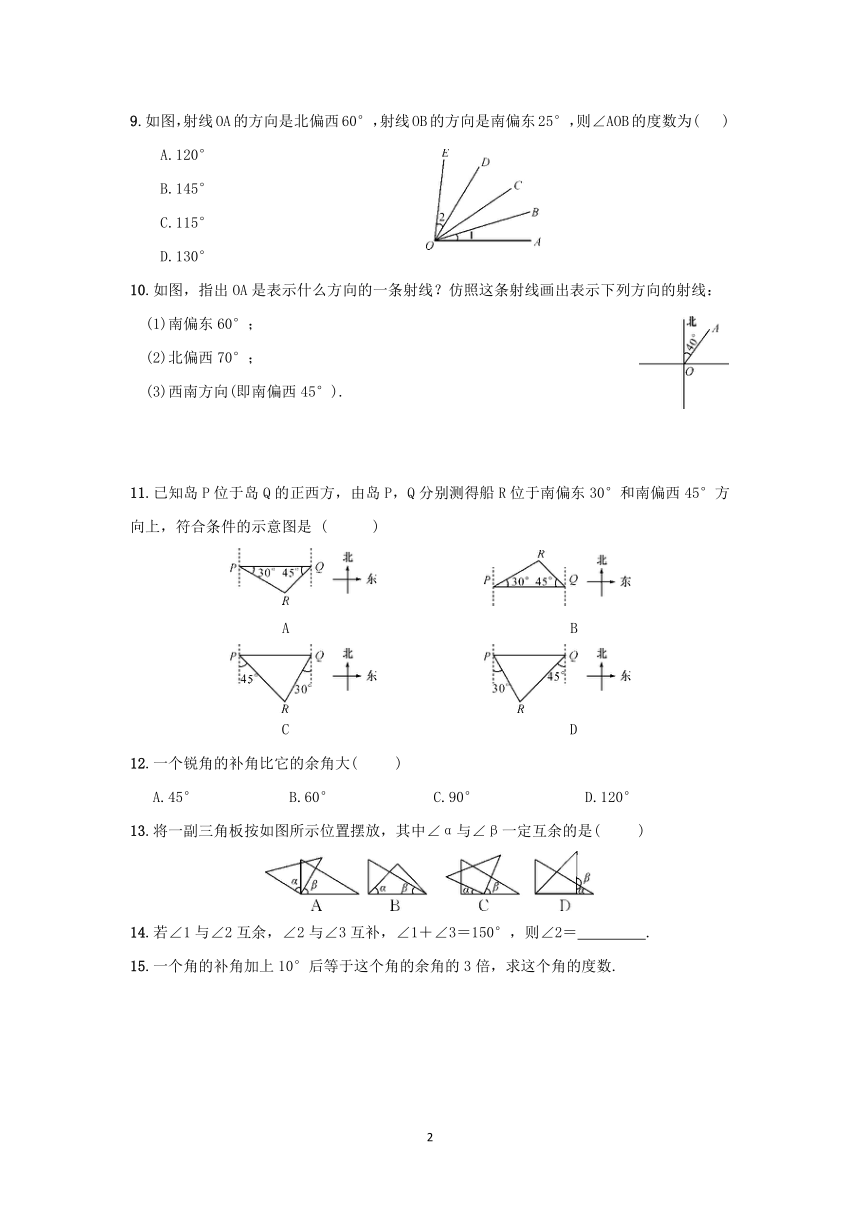
9.如图,射线OA的方向是北偏西60°,射线OB的方向是南偏东25°,则∠AOB的度数为( )
2607310106680A.120°
B.145°
C.115°
D.130°
10.如图,指出OA是表示什么方向的一条射线?仿照这条射线画出表示下列方向的射线:
448183083820(1)南偏东60°;
(2)北偏西70°;
(3)西南方向(即南偏西45°).
11.已知岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是 ( )
A B
C D
12.一个锐角的补角比它的余角大( )
A.45° B.60° C.90° D.120°
13.将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )
14.若∠1与∠2互余,∠2与∠3互补,∠1+∠3=150°,则∠2= .
15.一个角的补角加上10°后等于这个角的余角的3倍,求这个角的度数.
16.如图,OD平分∠BOC,OE平分∠AOC,∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
17.如图1所示,∠AOB,∠COD都是直角.
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系,并用推理的方法说明你的猜想是合理的;
(2)当∠COD绕着点O旋转到图2所示位置时,你在(1)中的猜想还成立吗?请证明你的结论.
参考答案:
1.D
2.B
3.A
4. 145°.
5. 19°21′.
6.解:(1)设这个角的度数是x°,根据题意,得
x=(90-x).
解得x=30.
所以这个角的度数是30°.
(2)因为OD平分∠AOB,
所以∠2=∠AOB=×114°=57°.
又因为∠1和∠2互余,
所以∠1=90°-∠2=90°-57°=33°.
7.D
8.B
9.B
10.解:OA表示北偏东40°.
(1)(2)(3)画图略.
11.D
12.C
13.C
14.60°.
15.解:设这个角为x°,则它的余角为90°-x°,补角为180°-x°,根据题意,得
180°-x°+10°=3×(90°-x°).
解得x=40.
答:这个角为40°.
16.解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
其补角为180°-∠AOB=180°-120°=60°.
(2)∠DOC=∠BOC=×70°=35°,
∠AOE=∠AOC=×50°=25°.
∠DOE与∠AOB互补.
理由:因为∠DOE=∠DOC+∠COE=35°+25°=60°,
所以∠DOE+∠AOB=60°+120°=180°.
故∠DOE与∠AOB互补.
17.解:(1)∠AOD与∠COB互补.
理由:因为∠AOB、∠COD都是直角,
所以∠AOB=∠COD=90°.
所以∠BOD=∠AOD-∠AOB=∠AOD-90°,∠BOD=∠COD-∠COB=90°-∠COB.
所以∠AOD-90°=90°-∠COB.
所以∠AOD+∠COB=180°.
所以∠AOD与∠COB互补.
(2)成立.证明:
因为∠AOB,∠COD都是直角,
所以∠AOB=∠COD=90°.
因为∠AOB+∠BOC+∠COD+∠AOD=360°,
所以∠AOD+∠COB=180°.
所以∠AOD与∠COB互补.
1.如果α与β互为余角,那么( )
A.α+β=180° B.α-β=180°
C.α-β=90° D.α+β=90°
2.已知∠A=55°,则它的余角是( )
A.25° B.35°
C.45° D.55°
3.如图,直线a与直线c相交于点O,∠1的余角的度数是( )
A.60° B.50°
C.40° D.30°
4.若∠α=35°,则∠α的补角为 .
5.一个角是70°39′,则它的余角的度数是 .
6.(1)已知一个角是它的余角的一半,求这个角的度数;
(2)如图,∠AOB=114°,OD是∠AOB的平分线,∠1与∠2互余,求∠1的度数.
7.已知∠1+∠2=180°,∠3+∠4=180°,如果∠1=∠3,那么∠2=∠4,依据是( )
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等 D.等角的补角相等
8.已知∠A与∠B互余,∠B与∠C互余,则∠A与∠C( )
A.互余 B.相等
C.互补 D.差为90°
9.如图,射线OA的方向是北偏西60°,射线OB的方向是南偏东25°,则∠AOB的度数为( )
2607310106680A.120°
B.145°
C.115°
D.130°
10.如图,指出OA是表示什么方向的一条射线?仿照这条射线画出表示下列方向的射线:
448183083820(1)南偏东60°;
(2)北偏西70°;
(3)西南方向(即南偏西45°).
11.已知岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是 ( )
A B
C D
12.一个锐角的补角比它的余角大( )
A.45° B.60° C.90° D.120°
13.将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )
14.若∠1与∠2互余,∠2与∠3互补,∠1+∠3=150°,则∠2= .
15.一个角的补角加上10°后等于这个角的余角的3倍,求这个角的度数.
16.如图,OD平分∠BOC,OE平分∠AOC,∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
17.如图1所示,∠AOB,∠COD都是直角.
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系,并用推理的方法说明你的猜想是合理的;
(2)当∠COD绕着点O旋转到图2所示位置时,你在(1)中的猜想还成立吗?请证明你的结论.
参考答案:
1.D
2.B
3.A
4. 145°.
5. 19°21′.
6.解:(1)设这个角的度数是x°,根据题意,得
x=(90-x).
解得x=30.
所以这个角的度数是30°.
(2)因为OD平分∠AOB,
所以∠2=∠AOB=×114°=57°.
又因为∠1和∠2互余,
所以∠1=90°-∠2=90°-57°=33°.
7.D
8.B
9.B
10.解:OA表示北偏东40°.
(1)(2)(3)画图略.
11.D
12.C
13.C
14.60°.
15.解:设这个角为x°,则它的余角为90°-x°,补角为180°-x°,根据题意,得
180°-x°+10°=3×(90°-x°).
解得x=40.
答:这个角为40°.
16.解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
其补角为180°-∠AOB=180°-120°=60°.
(2)∠DOC=∠BOC=×70°=35°,
∠AOE=∠AOC=×50°=25°.
∠DOE与∠AOB互补.
理由:因为∠DOE=∠DOC+∠COE=35°+25°=60°,
所以∠DOE+∠AOB=60°+120°=180°.
故∠DOE与∠AOB互补.
17.解:(1)∠AOD与∠COB互补.
理由:因为∠AOB、∠COD都是直角,
所以∠AOB=∠COD=90°.
所以∠BOD=∠AOD-∠AOB=∠AOD-90°,∠BOD=∠COD-∠COB=90°-∠COB.
所以∠AOD-90°=90°-∠COB.
所以∠AOD+∠COB=180°.
所以∠AOD与∠COB互补.
(2)成立.证明:
因为∠AOB,∠COD都是直角,
所以∠AOB=∠COD=90°.
因为∠AOB+∠BOC+∠COD+∠AOD=360°,
所以∠AOD+∠COB=180°.
所以∠AOD与∠COB互补.
