人教A版数学必修五1.1.1 正弦定理 讲授课件(23张PPT)
文档属性
| 名称 | 人教A版数学必修五1.1.1 正弦定理 讲授课件(23张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 12.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览








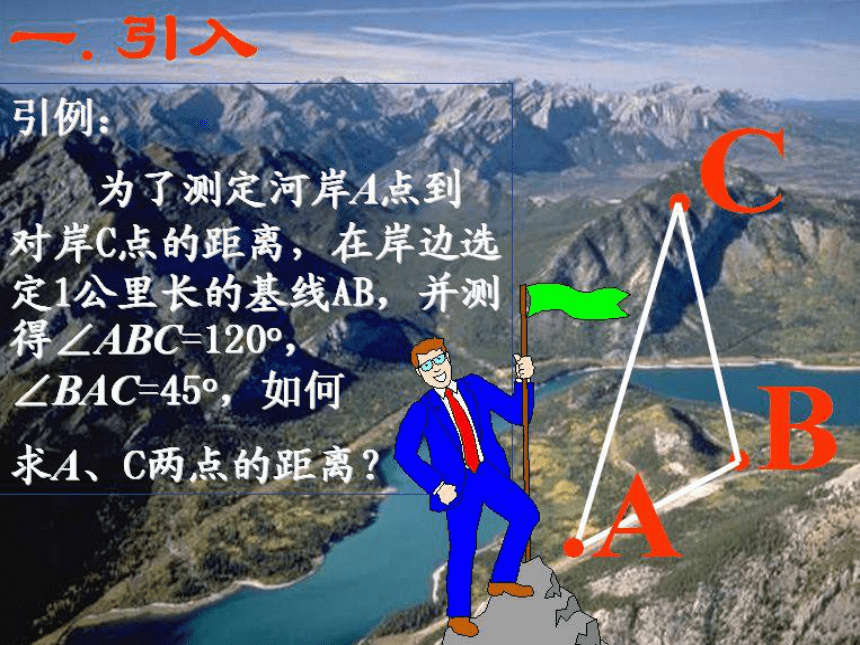
文档简介
1.1 正弦定理
第一章解三角形
第一节:正弦定理和余弦定理
1.1.1:正弦定理
教学目标
1.通过对特殊三角形边角间数量关系的探究发现正弦定理,初步学会运用由特殊到一般的思想方法发现数学规律.
2.能利用正弦定理解决两类解三角形的基本问题.
教学重难点
重点:理解正弦定理的推导过程,掌握正弦定理。
难点(1)能简单应用正弦定理来求三角形的边或角。
(2)已知两边和其中一边的对角解三角形时判断解的个数。
自主测试
3.在一个三角形中,各边和它所对角的正弦的比相等,即
?
1.三角形中大边对大角
2.在△ABC中,A+B+C=
4.△ABC中下列等式一定成立的是(C )
A asinA=bsinB B acosA=bcosB
C asinB=bsinA D acosB=bcosA
5. 在 ABC中,角A,B,C所对的边长分别为a,b,c,若 a=4,
b=3,A=120 ,则sinB=
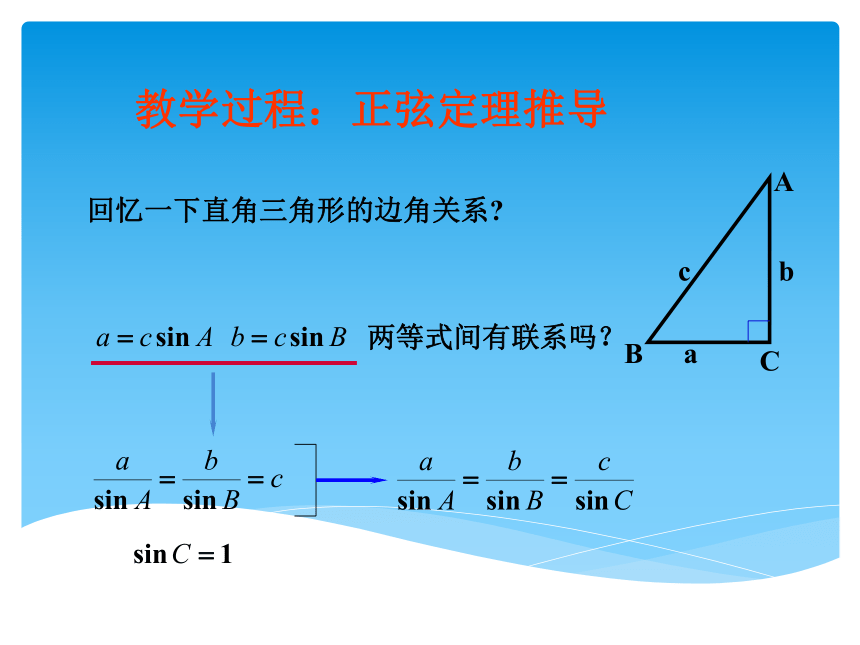
回忆一下直角三角形的边角关系?
A
B
C
c
b
a
两等式间有联系吗?
教学过程:正弦定理推导
csinB=bsinC
同理可得
D
过点A作AD⊥BC于D,
此时有
若三角形是锐角三角形, 如图1,
若三角形是钝角三角形, 如图2,
A
c
b
C
B
图1
a
sinB=
AD
c
sinC=
AD
b
则
AD=
C
A
c
b
B
图2
a
正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,
即
注:
要牢记哟!
边和它所对角的正弦比相等,
每个等式可视为一个方程,知三求其他
一般地,把三角形的三个角A,B,C和他们的边a,b,c叫做三角形的元素,已知三角形的几个元素,求其他元素的过程叫做解三角形.
利用正弦定理可以解决一些怎样的解 三角形问题呢?
题型探究——典例剖析 举一反三
题型一:已知两角及一边解三角形
例1.在△ABC中,已知A=45°,B=30°,a=2,求出其他边和角的大小.
跟踪训练1.在△ABC中,已a=8,B=60°,C=75°,
求A,b,c.
题后反思 已知三角形中的两边和其中一边的对角,解三角形时对解的情况进行讨论(1)首先由正弦定理求出另一边对角的正弦值.(2)如果已知的角为大边所对的角时,由三角形中大边对大角,大角对大边的法则能判断另一边所对的角为锐角,由正弦值可求锐角唯一.(3)如果已知的角为小边所对的角时,则不能判断另一边所对的角为锐角,这时由正弦值可求两个角,要分类讨论.
课堂小结
正弦定理表达了三角形的边和角的关系,是解三角形的重要工具.利用正弦定理可以解以下两类三角形:
(1)已知两角和任一边,求未知边和角;
(2)已知两边和其中一边的对角,求另一边的对角,从而进一步求出其他的边和角,此类问题的解需要进行讨论.
课后作业
1.在 ABC中,角A,B,C所对的边长分别为a,b,c,且A︰B︰C= 1︰2︰3,且c=6
(1)求角A,B,C的度数
(2)求a,b的值
2.等腰 ABC中,顶角A=120, 腰长AB=1,求底边长。
3. 在 ABC中,角A,B,C所对的边长分别为a,b,c,若 a=4,b=3,A=120,则sinB=
4. 在 ABC中,角A,B,C所对的边长分别为a,b,c,已知A=75,B=45,b=4 ,求c的长。
第一章解三角形
第一节:正弦定理和余弦定理
1.1.1:正弦定理
教学目标
1.通过对特殊三角形边角间数量关系的探究发现正弦定理,初步学会运用由特殊到一般的思想方法发现数学规律.
2.能利用正弦定理解决两类解三角形的基本问题.
教学重难点
重点:理解正弦定理的推导过程,掌握正弦定理。
难点(1)能简单应用正弦定理来求三角形的边或角。
(2)已知两边和其中一边的对角解三角形时判断解的个数。
自主测试
3.在一个三角形中,各边和它所对角的正弦的比相等,即
?
1.三角形中大边对大角
2.在△ABC中,A+B+C=
4.△ABC中下列等式一定成立的是(C )
A asinA=bsinB B acosA=bcosB
C asinB=bsinA D acosB=bcosA
5. 在 ABC中,角A,B,C所对的边长分别为a,b,c,若 a=4,
b=3,A=120 ,则sinB=
回忆一下直角三角形的边角关系?
A
B
C
c
b
a
两等式间有联系吗?
教学过程:正弦定理推导
csinB=bsinC
同理可得
D
过点A作AD⊥BC于D,
此时有
若三角形是锐角三角形, 如图1,
若三角形是钝角三角形, 如图2,
A
c
b
C
B
图1
a
sinB=
AD
c
sinC=
AD
b
则
AD=
C
A
c
b
B
图2
a
正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,
即
注:
要牢记哟!
边和它所对角的正弦比相等,
每个等式可视为一个方程,知三求其他
一般地,把三角形的三个角A,B,C和他们的边a,b,c叫做三角形的元素,已知三角形的几个元素,求其他元素的过程叫做解三角形.
利用正弦定理可以解决一些怎样的解 三角形问题呢?
题型探究——典例剖析 举一反三
题型一:已知两角及一边解三角形
例1.在△ABC中,已知A=45°,B=30°,a=2,求出其他边和角的大小.
跟踪训练1.在△ABC中,已a=8,B=60°,C=75°,
求A,b,c.
题后反思 已知三角形中的两边和其中一边的对角,解三角形时对解的情况进行讨论(1)首先由正弦定理求出另一边对角的正弦值.(2)如果已知的角为大边所对的角时,由三角形中大边对大角,大角对大边的法则能判断另一边所对的角为锐角,由正弦值可求锐角唯一.(3)如果已知的角为小边所对的角时,则不能判断另一边所对的角为锐角,这时由正弦值可求两个角,要分类讨论.
课堂小结
正弦定理表达了三角形的边和角的关系,是解三角形的重要工具.利用正弦定理可以解以下两类三角形:
(1)已知两角和任一边,求未知边和角;
(2)已知两边和其中一边的对角,求另一边的对角,从而进一步求出其他的边和角,此类问题的解需要进行讨论.
课后作业
1.在 ABC中,角A,B,C所对的边长分别为a,b,c,且A︰B︰C= 1︰2︰3,且c=6
(1)求角A,B,C的度数
(2)求a,b的值
2.等腰 ABC中,顶角A=120, 腰长AB=1,求底边长。
3. 在 ABC中,角A,B,C所对的边长分别为a,b,c,若 a=4,b=3,A=120,则sinB=
4. 在 ABC中,角A,B,C所对的边长分别为a,b,c,已知A=75,B=45,b=4 ,求c的长。
