高中数学人教版A版必修2教学课件:2.2.2平面与平面平行的判定(20张PPT)
文档属性
| 名称 | 高中数学人教版A版必修2教学课件:2.2.2平面与平面平行的判定(20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 997.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:13:44 | ||
图片预览




文档简介
平面与平面平行的判定
α
β
1.判定线面平行的方法有哪些呢?
2.判定定理体现了什么样的转化思想?
温故知新
α
a
b
(1)定义法
(2)判定定理
线线平行
线面平行
空间问题平面化
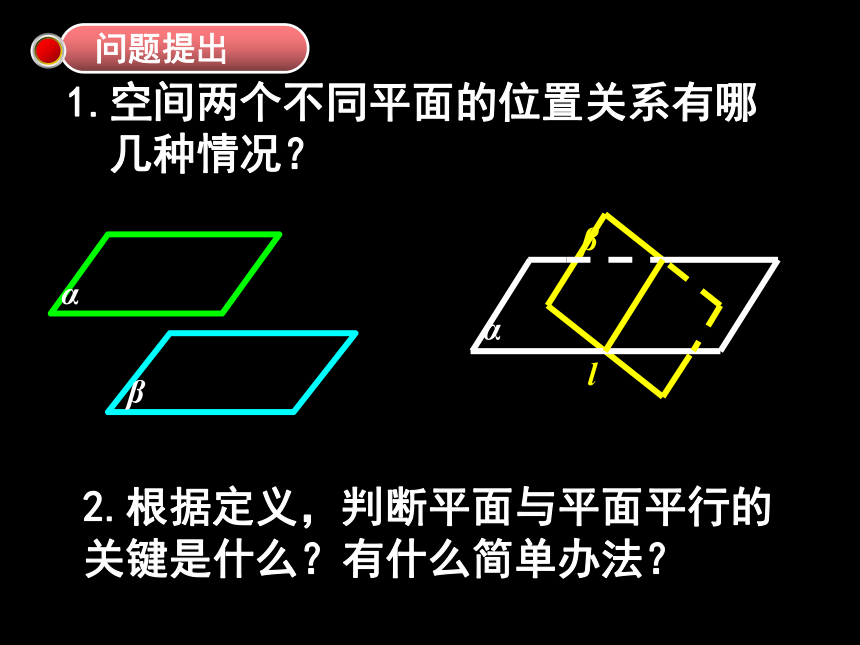
1.空间两个不同平面的位置关系有哪
几种情况?
2.根据定义,判断平面与平面平行的
关键是什么?有什么简单办法?
问题提出
α
β
l
α
β
知识探究(一):平面与平面平行的背景分析
思考1:若两个平面平行,那么其中一个平面内的直线与另一个平面位置关系如何?为什么?
思考2: 若一个平面内的所有直线都与另一个平面平行,那么这两个平面会平行?
归纳:判定两个平面平行的问题可转化为直线与
平面平行的问题来解决,那么最少需要几条直线
与平面平行呢?
α
β
a
α
β
l
P
a
假设不平行(即相交)
矛盾
知识探究(二):平面与平面平行的判定
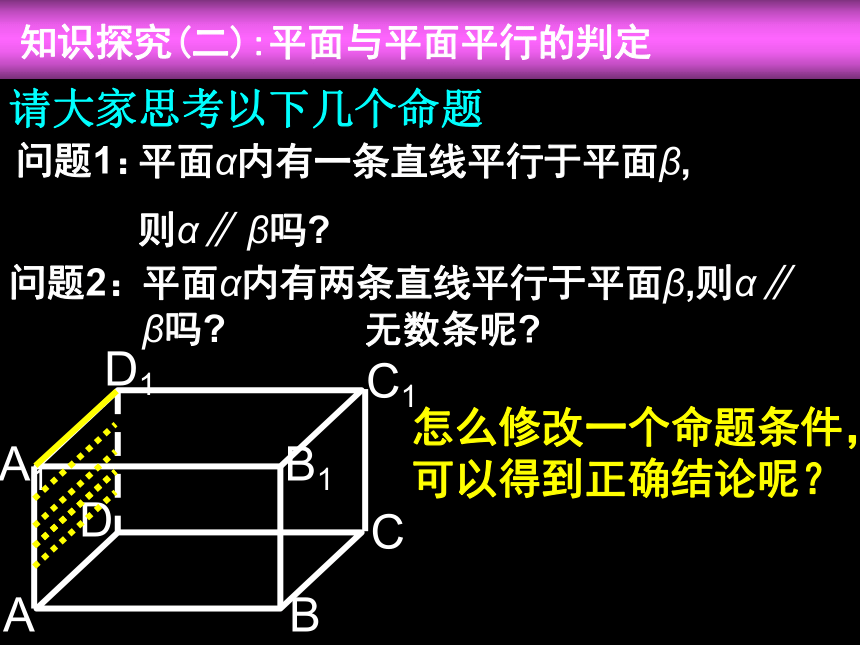
请大家思考以下几个命题
平面α内有一条直线平行于平面β,
则α∥ β吗?
问题1:
问题2:
平面α内有两条直线平行于平面β,则α∥ β吗?
无数条呢?
A
B
C
D
A1
B1
C1
D1
怎么修改一个命题条件,
可以得到正确结论呢?
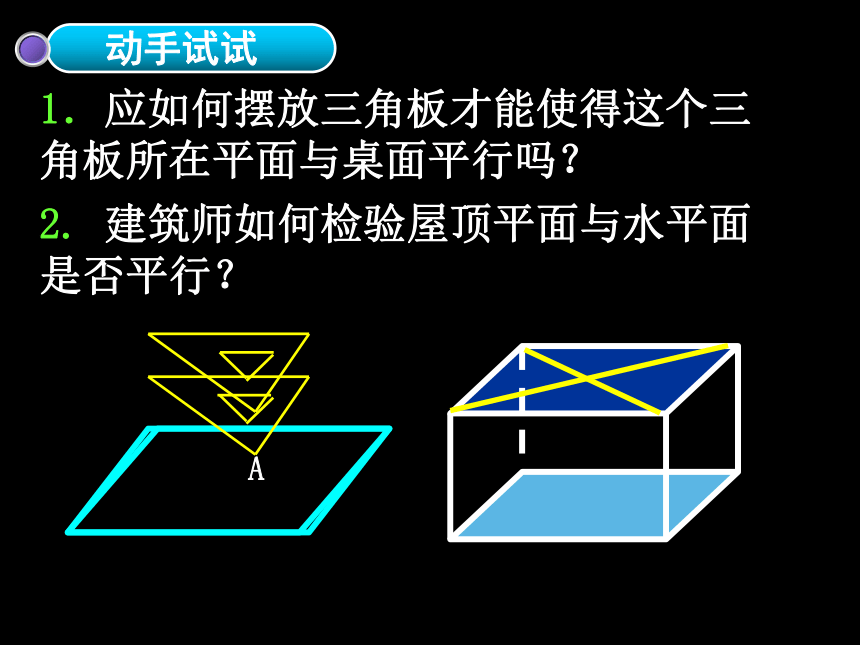
1.应如何摆放三角板才能使得这个三角板所在平面与桌面平行吗?
A
动手试试
2. 建筑师如何检验屋顶平面与水平面
是否平行?
平面与平面平行的判定定理
a
b
α
β
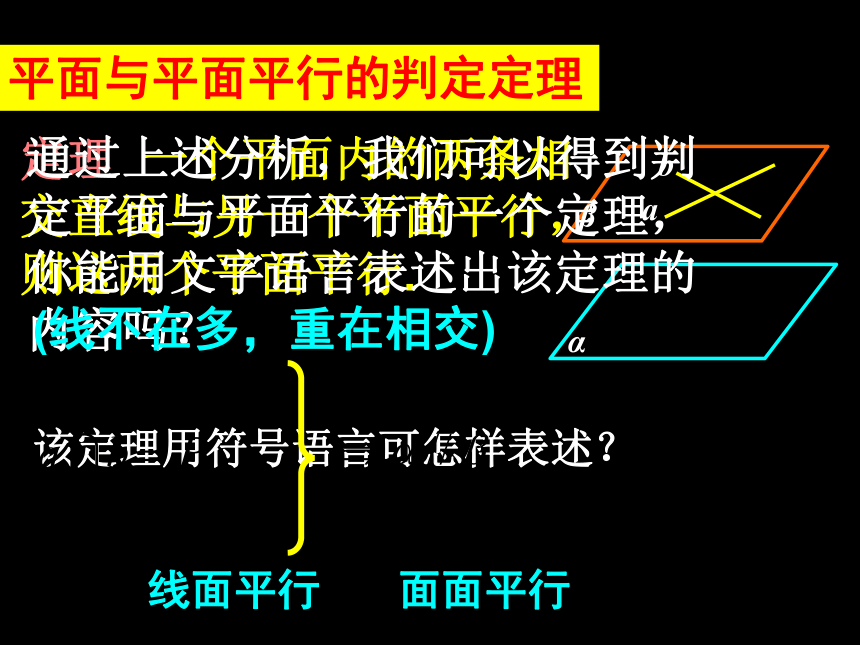
定理 一个平面内的两条相
交直线与另一个平面平行,
则这两个平面平行.
通过上述分析,我们可以得到判定平面与平面平行的一个定理,你能用文字语言表述出该定理的内容吗?
该定理用符号语言可怎样表述?
(线不在多,重在相交)
线面平行
面面平行
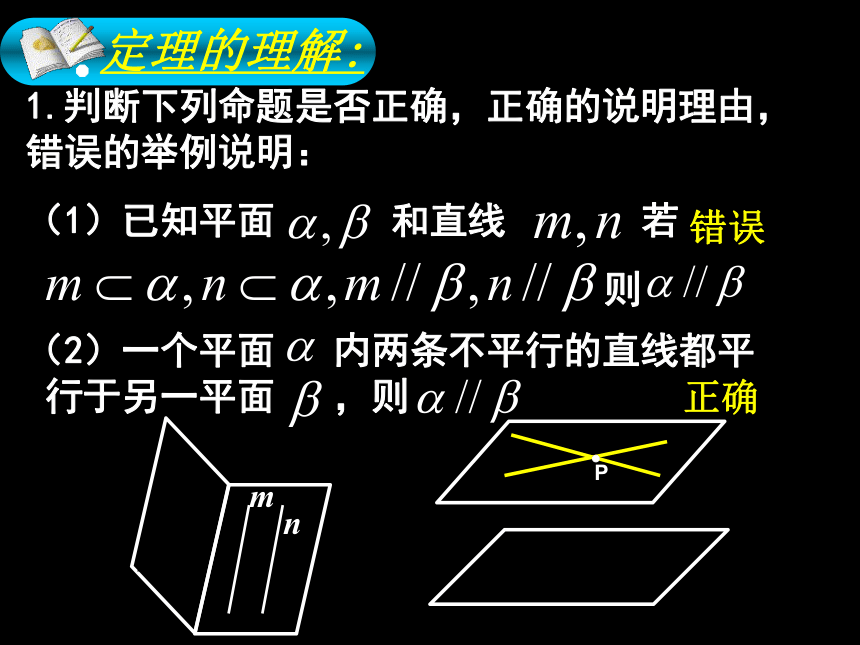
定理的理解:
1.判断下列命题是否正确,正确的说明理由,错误的举例说明:
(1)已知平面 和直线 若
则
(2)一个平面 内两条不平行的直线都平
行于另一平面 ,则
错误
正确
m
n
P
2.平面和平面平行的条件可以是( )
(A) 内有无数多条直线都与 平行
(B)直线
(C)直线 ,直线 ,且
(D) 内的任何一条直线都与 平行
D
定理的理解:
例1 在正方体ABCD-A1B1C1D1中. 求证:
平面AB1D1∥平面BC1D.
B
A
A1
B1
C1
D1
C
D
理论迁移
平行四边形ABC1D1
矩形BB1D1D
B
A
A1
B1
C1
D1
C
D
∵C1D1 ∥A1B1, C1D1=A1B1
又AB∥A1B1, AB=A1B1
∴AB∥D1C1, AB=D1C1
∴D1C1BA为平行四边形
∴D1A ∥C1B
∴D1A ∥平面C1BD
同理D1B1 ∥平面C1BD
又D1A D1B=D1
∴平面AB1D1∥平面BC1D.
又D1A 平面C1BD,C1B 平面C1BD
[拓展1]M,N分别为AA1,CC1的中点,
判断平面NBD与平面MB1D1 的位置关系?
B
A
A1
B1
C1
D1
C
D
M
N
关键:找两组线对应平行.
上述判断面面平行的关键是什么?
[拓展2]P,Q,R分别为AA1,AB,AD的中点
判断平面PQR与平面CB1D1位置关系?
B
A
A1
B1
C1
D1
C
D
P
Q
R
[拓展3]M,N,E,F分别为A1B1,A1D1,
B1C1,C1D1的中点,求证:
平面AMN∥平面EFDB
B
A
A1
B1
C1
D1
C
D
M
N
F
E
[拓展4] S,E,F,G分别为B1D1,BC,DC,
SC的中点,求证:平面EFG∥平面BDD1B1
B
A
A1
B1
C1
D1
C
D
S
G
F
E
O
O1
如图三棱柱,点D为AC的中点,
D1为A1C1上的点,问:当A1D1:D1C1
为何值时,平面BC1D∥平面AB1D1? 此时 BC1与平面AB1D1的位置关系如何?
D
A
B
C
A1
B1
C1
D1
想一想
D1
几何画板演示
请先安装几何画板4.07或以上版本
例2 在三棱锥P-ABC中,PD:PA=PE:PB
=PF:PC=1:3(1)求证:平面DEF//平面ABC
(2)求S△DEF: S△ABC
P
A
B
C
D
E
F
例3四棱锥P-ABCD中,底面为平行四边形,PM:MA=BN:ND=PQ:QD 求证:
平面BNQ∥平面PBC
A
B
D
C
M
N
Q
P
1.面面平行,通常可以转化为线面平行来处理.
反思~领悟
2、证明的书写三个条件“内”、“交”、
“平行”,缺一不可。
线线平行
线面平行
面面平行
基本思路:
作业:
P58练习:1, 3(做书上)
P62习题:7,8.
α
β
1.判定线面平行的方法有哪些呢?
2.判定定理体现了什么样的转化思想?
温故知新
α
a
b
(1)定义法
(2)判定定理
线线平行
线面平行
空间问题平面化
1.空间两个不同平面的位置关系有哪
几种情况?
2.根据定义,判断平面与平面平行的
关键是什么?有什么简单办法?
问题提出
α
β
l
α
β
知识探究(一):平面与平面平行的背景分析
思考1:若两个平面平行,那么其中一个平面内的直线与另一个平面位置关系如何?为什么?
思考2: 若一个平面内的所有直线都与另一个平面平行,那么这两个平面会平行?
归纳:判定两个平面平行的问题可转化为直线与
平面平行的问题来解决,那么最少需要几条直线
与平面平行呢?
α
β
a
α
β
l
P
a
假设不平行(即相交)
矛盾
知识探究(二):平面与平面平行的判定
请大家思考以下几个命题
平面α内有一条直线平行于平面β,
则α∥ β吗?
问题1:
问题2:
平面α内有两条直线平行于平面β,则α∥ β吗?
无数条呢?
A
B
C
D
A1
B1
C1
D1
怎么修改一个命题条件,
可以得到正确结论呢?
1.应如何摆放三角板才能使得这个三角板所在平面与桌面平行吗?
A
动手试试
2. 建筑师如何检验屋顶平面与水平面
是否平行?
平面与平面平行的判定定理
a
b
α
β
定理 一个平面内的两条相
交直线与另一个平面平行,
则这两个平面平行.
通过上述分析,我们可以得到判定平面与平面平行的一个定理,你能用文字语言表述出该定理的内容吗?
该定理用符号语言可怎样表述?
(线不在多,重在相交)
线面平行
面面平行
定理的理解:
1.判断下列命题是否正确,正确的说明理由,错误的举例说明:
(1)已知平面 和直线 若
则
(2)一个平面 内两条不平行的直线都平
行于另一平面 ,则
错误
正确
m
n
P
2.平面和平面平行的条件可以是( )
(A) 内有无数多条直线都与 平行
(B)直线
(C)直线 ,直线 ,且
(D) 内的任何一条直线都与 平行
D
定理的理解:
例1 在正方体ABCD-A1B1C1D1中. 求证:
平面AB1D1∥平面BC1D.
B
A
A1
B1
C1
D1
C
D
理论迁移
平行四边形ABC1D1
矩形BB1D1D
B
A
A1
B1
C1
D1
C
D
∵C1D1 ∥A1B1, C1D1=A1B1
又AB∥A1B1, AB=A1B1
∴AB∥D1C1, AB=D1C1
∴D1C1BA为平行四边形
∴D1A ∥C1B
∴D1A ∥平面C1BD
同理D1B1 ∥平面C1BD
又D1A D1B=D1
∴平面AB1D1∥平面BC1D.
又D1A 平面C1BD,C1B 平面C1BD
[拓展1]M,N分别为AA1,CC1的中点,
判断平面NBD与平面MB1D1 的位置关系?
B
A
A1
B1
C1
D1
C
D
M
N
关键:找两组线对应平行.
上述判断面面平行的关键是什么?
[拓展2]P,Q,R分别为AA1,AB,AD的中点
判断平面PQR与平面CB1D1位置关系?
B
A
A1
B1
C1
D1
C
D
P
Q
R
[拓展3]M,N,E,F分别为A1B1,A1D1,
B1C1,C1D1的中点,求证:
平面AMN∥平面EFDB
B
A
A1
B1
C1
D1
C
D
M
N
F
E
[拓展4] S,E,F,G分别为B1D1,BC,DC,
SC的中点,求证:平面EFG∥平面BDD1B1
B
A
A1
B1
C1
D1
C
D
S
G
F
E
O
O1
如图三棱柱,点D为AC的中点,
D1为A1C1上的点,问:当A1D1:D1C1
为何值时,平面BC1D∥平面AB1D1? 此时 BC1与平面AB1D1的位置关系如何?
D
A
B
C
A1
B1
C1
D1
想一想
D1
几何画板演示
请先安装几何画板4.07或以上版本
例2 在三棱锥P-ABC中,PD:PA=PE:PB
=PF:PC=1:3(1)求证:平面DEF//平面ABC
(2)求S△DEF: S△ABC
P
A
B
C
D
E
F
例3四棱锥P-ABCD中,底面为平行四边形,PM:MA=BN:ND=PQ:QD 求证:
平面BNQ∥平面PBC
A
B
D
C
M
N
Q
P
1.面面平行,通常可以转化为线面平行来处理.
反思~领悟
2、证明的书写三个条件“内”、“交”、
“平行”,缺一不可。
线线平行
线面平行
面面平行
基本思路:
作业:
P58练习:1, 3(做书上)
P62习题:7,8.
