2020--2021学年北京市九中九年级数学周测2--相似三角形(word版含答案)
文档属性
| 名称 | 2020--2021学年北京市九中九年级数学周测2--相似三角形(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 154.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 11:38:17 | ||
图片预览


文档简介
初三年级数学周测2--相似三角形
注:第1—12题每空4分,共60分;第13—16题每题10分,共40分;本卷满分100分。
1.在比例尺为1:2000的地图上测得AB两地间的图上距离为5cm,则AB两地间的实际距离为__________m.
答案:100
2.在等腰△ABC和等腰△DEF中,∠A与∠D是顶角,下列说法正确的有__________
①∠A=∠D时,两三角形相似;
②∠A=∠E时,两三角形相似;
③时,两三角形相似;
④∠B=∠E时,两三角形相似;
答案:①②③
3.如图,已知DE//BC,△ABC∽△ADE,则∠ABC=__________,=__________=__________
答案:∠ADE,,
第3题图
第8题图
第9题图
4.如果两个相似三角形对应高的比为4:5,则这两个三角形的相似比是__________,它们的面积的比是__________
答案:4:5;16:25
5.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是__________
答案:24
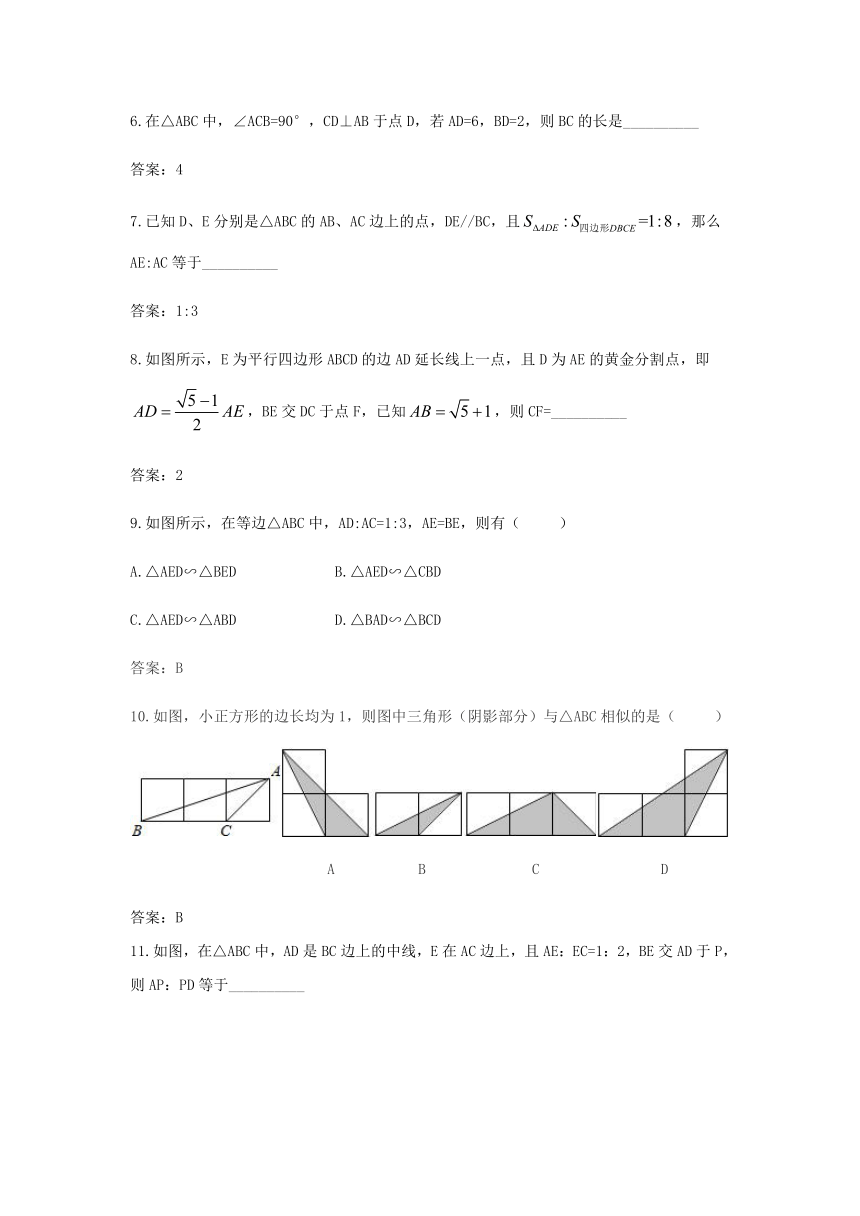
6.在△ABC中,∠ACB=90°,CD⊥AB于点D,若AD=6,BD=2,则BC的长是__________
答案:4
7.已知D、E分别是△ABC的AB、AC边上的点,DE//BC,且,那么AE:AC等于__________
答案:1:3
8.如图所示,E为平行四边形ABCD的边AD延长线上一点,且D为AE的黄金分割点,即,BE交DC于点F,已知,则CF=__________
答案:2
9.如图所示,在等边△ABC中,AD:AC=1:3,AE=BE,则有(
)
A.△AED∽△BED
B.△AED∽△CBD
C.△AED∽△ABD
D.△BAD∽△BCD
答案:B
10.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是(
)
A
B
C
D
答案:B
11.如图,在△ABC中,AD是BC边上的中线,E在AC边上,且AE:EC=1:2,BE交AD于P,则AP:PD等于__________
答案:1:1
12.如图所示,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3,若△A2B1B2、△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为__________
答案:10.5
13.如图所示,点D在AB上,且DE//BC,交AC于E,点F在AD上,且AD?=AF·AB.求证:△AEF∽△ACD
答案:证明:
∵AD?=AF×AB
∴AD/AB=AF/AD
∵DE‖BC
∴△ADE∽△ABC
∴AD/AB
=AE/AC
∴AF/AD=AE/AC
∵∠A=∠A
∴△AEF∽△ACD
14.如图,在边长为1的小正方形组成的网格中,,△ABC和△DEF的顶点都在格点上.P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)判断△ABC和△DEF是否相似,并说明理由;
(2)
画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:保留痕迹,不写作法与证明).
答案:
(1)△ABC和△DEF相似.理由如下:
根据勾股定理,得AB=2,AC=,BC=5,DE=4,DF=2,EF=2.
===,
∴△ABC∽△DEF;
(2)如图:连接P2P5,P2P4,P4P5,
∵P2P5=,P2P4=,P4P5=2,AB=2,AC=,BC=5,
∴===,
∴△ABC∽△P2P4P5.
15.如图,在△ABC中,AC=8cm,BC=16cm,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?
答案:
16.如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC.(AB>AE).
(1)△AEF与△ECF是否相似?若相似,证明你的结论;若不相似,请说明理由;
(2)设=k,是否存在这样的k值,使得△AEF与△BFC相似?若存在,证明你的结论并求出k的值;若不存在,说明理由.
注:第1—12题每空4分,共60分;第13—16题每题10分,共40分;本卷满分100分。
1.在比例尺为1:2000的地图上测得AB两地间的图上距离为5cm,则AB两地间的实际距离为__________m.
答案:100
2.在等腰△ABC和等腰△DEF中,∠A与∠D是顶角,下列说法正确的有__________
①∠A=∠D时,两三角形相似;
②∠A=∠E时,两三角形相似;
③时,两三角形相似;
④∠B=∠E时,两三角形相似;
答案:①②③
3.如图,已知DE//BC,△ABC∽△ADE,则∠ABC=__________,=__________=__________
答案:∠ADE,,
第3题图
第8题图
第9题图
4.如果两个相似三角形对应高的比为4:5,则这两个三角形的相似比是__________,它们的面积的比是__________
答案:4:5;16:25
5.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是__________
答案:24
6.在△ABC中,∠ACB=90°,CD⊥AB于点D,若AD=6,BD=2,则BC的长是__________
答案:4
7.已知D、E分别是△ABC的AB、AC边上的点,DE//BC,且,那么AE:AC等于__________
答案:1:3
8.如图所示,E为平行四边形ABCD的边AD延长线上一点,且D为AE的黄金分割点,即,BE交DC于点F,已知,则CF=__________
答案:2
9.如图所示,在等边△ABC中,AD:AC=1:3,AE=BE,则有(
)
A.△AED∽△BED
B.△AED∽△CBD
C.△AED∽△ABD
D.△BAD∽△BCD
答案:B
10.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是(
)
A
B
C
D
答案:B
11.如图,在△ABC中,AD是BC边上的中线,E在AC边上,且AE:EC=1:2,BE交AD于P,则AP:PD等于__________
答案:1:1
12.如图所示,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3,若△A2B1B2、△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为__________
答案:10.5
13.如图所示,点D在AB上,且DE//BC,交AC于E,点F在AD上,且AD?=AF·AB.求证:△AEF∽△ACD
答案:证明:
∵AD?=AF×AB
∴AD/AB=AF/AD
∵DE‖BC
∴△ADE∽△ABC
∴AD/AB
=AE/AC
∴AF/AD=AE/AC
∵∠A=∠A
∴△AEF∽△ACD
14.如图,在边长为1的小正方形组成的网格中,,△ABC和△DEF的顶点都在格点上.P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)判断△ABC和△DEF是否相似,并说明理由;
(2)
画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:保留痕迹,不写作法与证明).
答案:
(1)△ABC和△DEF相似.理由如下:
根据勾股定理,得AB=2,AC=,BC=5,DE=4,DF=2,EF=2.
===,
∴△ABC∽△DEF;
(2)如图:连接P2P5,P2P4,P4P5,
∵P2P5=,P2P4=,P4P5=2,AB=2,AC=,BC=5,
∴===,
∴△ABC∽△P2P4P5.
15.如图,在△ABC中,AC=8cm,BC=16cm,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?
答案:
16.如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC.(AB>AE).
(1)△AEF与△ECF是否相似?若相似,证明你的结论;若不相似,请说明理由;
(2)设=k,是否存在这样的k值,使得△AEF与△BFC相似?若存在,证明你的结论并求出k的值;若不存在,说明理由.
