反比例函数回顾与思考

(共43张PPT)
复习目标：
1、会根据反比例函数的主要性质解决问题
2、能在实际问题中建立反比例函数模型，进而解决问题
3、会用“数形结合”的思想与方法解决数学问题。
4、学会用数学语言与同伴交流，能阐述自己的观点。力争使自己由“会做”向“会讲”转变。
2、反比例函数的表示形式
y=kx-1
(K为常数，K≠0)
xy=k
我思我进步
(K为常数，K≠0)
(K为常数，K≠0)
1.反比例函数的定义:
一般地，如果两个变量x,y之间的关系可以表示成 (K为常数，K≠0）的形式，那么称y是x的反比例函数.
y=
k
x
① ② ③
④ ⑤ ⑥
y = 3x-1
y = 2x2
y =
2x
3
y = 3x
y =
1
3x
y =
x
1
下列函数中哪些是正比例函数？哪些是反比例函数
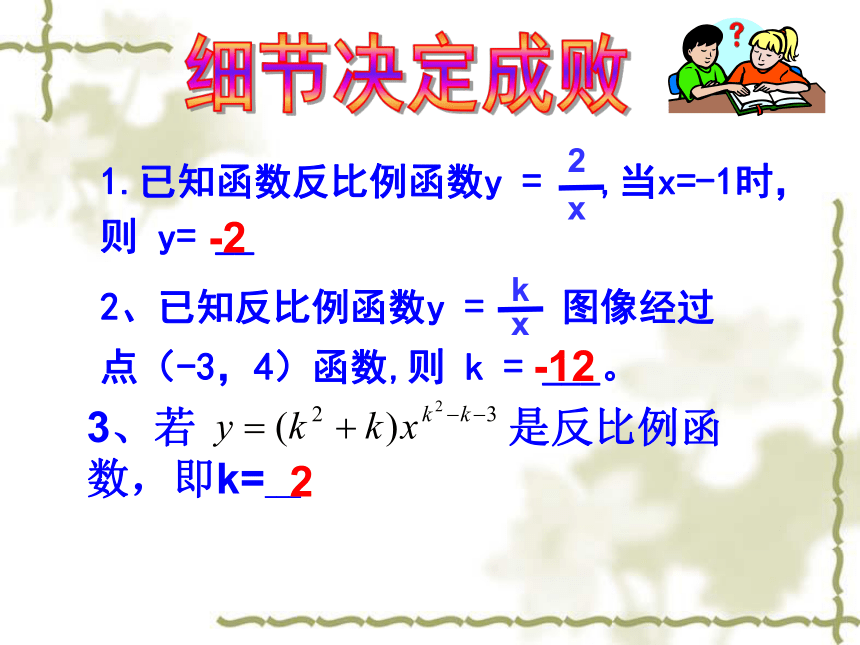
1.已知函数反比例函数y = ,当x=-1时，则 y= __
2、已知反比例函数y = 图像经过点（-3，4）函数,则 k = ___。
-2
-12
2
x
k
x
3、若 是反比例函数，即k=___
2
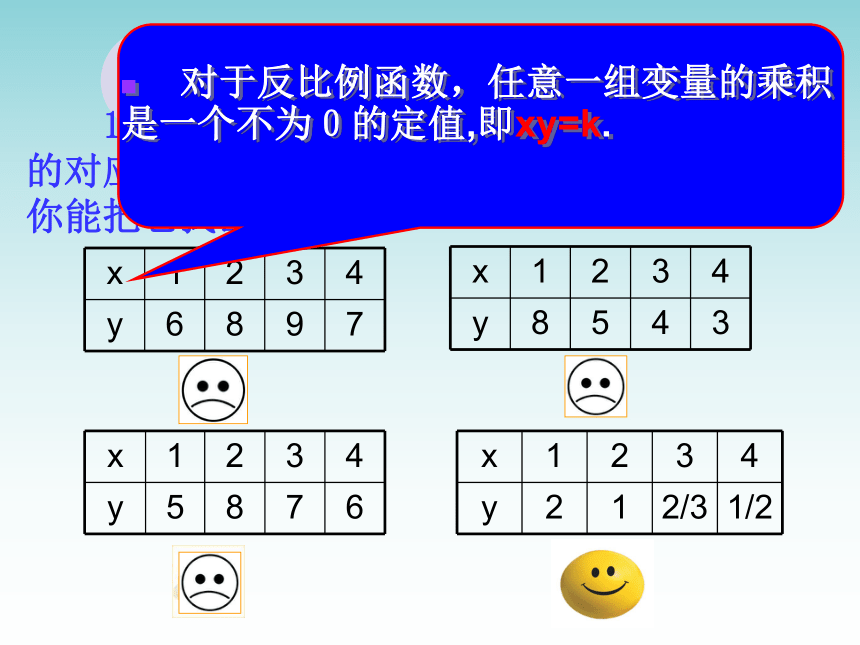
1.下列的数表中分别给出了变量y与x之间的对应关系，其中有一个表示的是反比例函数,你能把它找出来吗
(D)
x 1 2 3 4
y 6 8 9 7
x 1 2 3 4
y 8 5 4 3
x 1 2 3 4
y 5 8 7 6
x 1 2 3 4
y 2 1 2/3 1/2
对于反比例函数，任意一组变量的乘积是一个不为０的定值,即xy=k.
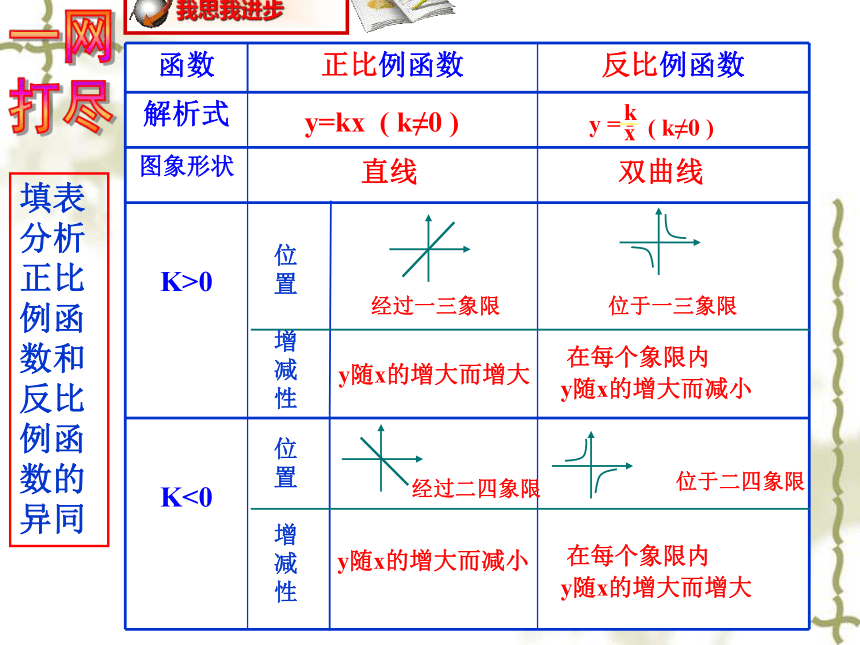
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k≠0 )
y =
x
k
直线
双曲线
经过一三象限
y随x的增大而增大
位于一三象限
在每个象限内
y随x的增大而减小
经过二四象限
位于二四象限
y随x的增大而减小
在每个象限内
y随x的增大而增大
填表分析正比例函数和反比例函数的异同
我思我进步
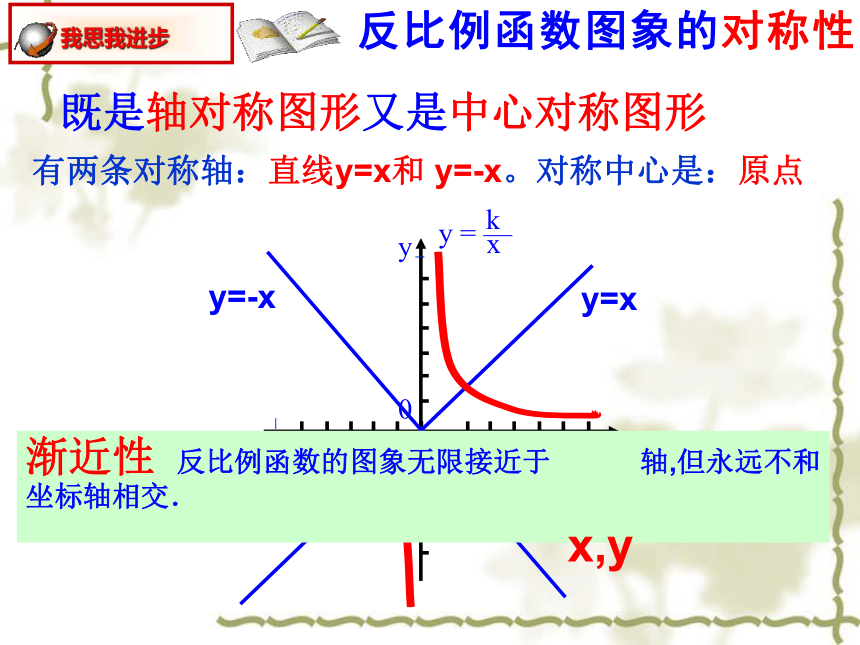
既是轴对称图形又是中心对称图形
x
y
0
1
2
y = —
k
x
y=x
y=-x
反比例函数图象的对称性
有两条对称轴：直线y=x和 y=-x。对称中心是：原点
我思我进步
渐近性　反比例函数的图象无限接近于　　 轴,但永远不和坐标轴相交．
x,y
已知点（－m,n）在反比例函数的图象上，则
它的图象也一定经过点__________
(m, －n)
小试 牛刀
学以致用
小试 牛刀
学以致用
若函数 是反比例函数，则k= ，图象经过 象限，在每个象限内，y随x的增大而
-2
第一，三
减小
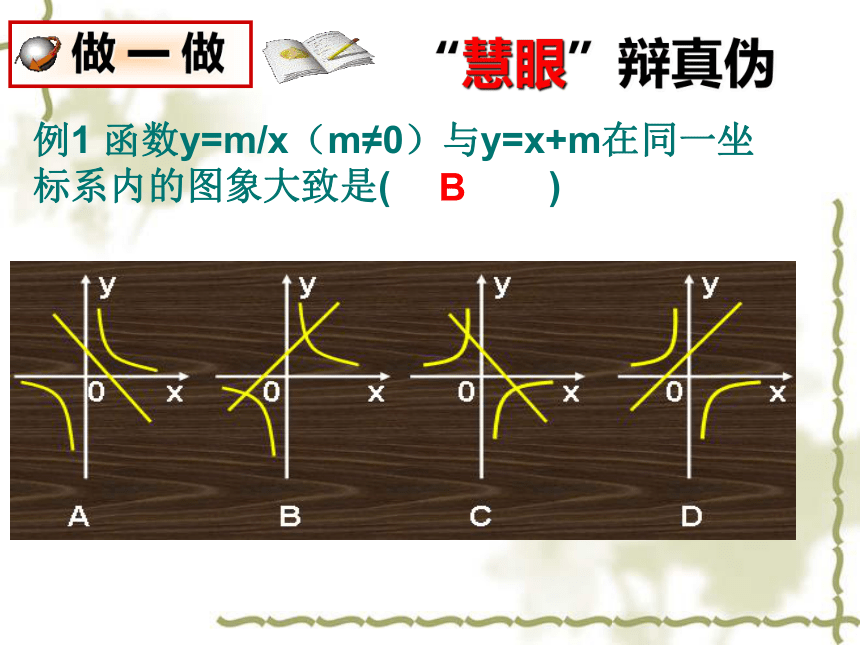
例1 函数y=m/x（m≠0）与y=x+m在同一坐标系内的图象大致是( )
B
做 一 做
“慧眼”辩真伪
2.两位同学在描述同一反比例函数的图象时,甲同学说:这个反比例函数图象上任意一点到两坐标轴的距离的积都是3;乙同学说:这个反比例函数的图象与直线y=x有两个交点,你认为这两位同学所描述的反比例函数的解析式是 ( )
A
做 一 做
“慧眼”辩真伪
（1）若点A(7,y1),B(5,y2)，则y1,y2的大小关系是: 。
若点A、B都在反比例函数的 图象上
（2）若点A(7,y1),B(-5,y2)，则y1,y2的大小关系是: 。
利用图像法或代入法。增减性，一定要考虑在每一象限内。
同一象限按增减，跨越象限怎么办？
函数 的图象上有三
点（－3,y1）, （－1,y2）, （2,y3）,则函
数值y1、y2、y3的大小关系___________;
y3< y1< y2
巩固提高，要认真动手动脑呦!
S矩形=|xy|=|k|
面积不变性：
S三角形= |xy|= |k|
1
2
1
2
P
A
o
y
x
P
A
o
y
x
(x,y)
(x,y)
B
如图,点P是x轴上的一个动点,过点P作x轴的垂线PQ,交双曲线于点Q,连结OQ, 当点P沿x轴正半方向运动时,Rt△QOP面积( )
A.逐渐增大
B.逐渐减小
C.保持不变
D.无法确定
x
y
o
p
p
p
p
p
p
p
p
p
c
如图所示，A（x1 ，y1）、B（x2 ，y2）、C（x3 ，y3）是函数y= 的图象在第一象限分支上的三个点，且 x1＜ x2 ＜ x3 ，过A、B、C三点分别作坐标轴的垂线，得矩形ADOH、BEON、CFOP，它们的面积分别为S1、S2、S3，则下列结论中正确的是( )
1
1
x
A、S1B、S3 C、S2< S3< S1
D、S1= S2 = S3
D
A.S = 1 B.1C.S = 2 D.S>2
A
C
o
y
x
B
C
变1
变2:换一个角度： 双曲线 上任一点分别作x轴、y轴的垂线段，与x轴y轴围成矩形面积为12，求函数解析式。
如图
∵︳K︱ ＝12
∴k=±12
(X>0)
先由数（式）到形再由形到数（式）的数学思想
变3.正比例函数y=x与反比例函数y=1/x的图象交于A，C两点,AB⊥ X轴于B，CD⊥ X轴于 D，则四边形ABCD的面积___　
2
正比例函数图象与反比例函数图象的交点问题一次函数y=kx+b与反比例函数y=
消去y后，关于x的一元二次方程的判别式△：
当△>0时，两函数图象有 交点；
当△=0时，两函数图象有 交点；
当△<0时，两函数图象 交点
我思我进步
4
两个
一个
无
例 如图：一次函数y=ax+b的图象与反比例函数
y= 交于M （2，m） 、N （-1，-4）两点
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出反比例函数的值大于一次函数的值的x的取值范围。
y
x
k
x
2
0
-1
N（-1，-4）
M（2，m）
我思我进步
4
（1）求反比例函数和一次函数的解析式；
y
x
2
0
-1
N（-1，-4）
M（2，m）
（1）∵点N（-1，-4）在反比例函数图象上
∴k=4, ∴y=
又∵点M（2，m）在反比例函数图象上
∴m=2 ∴m（2，2）
∵点M、N都y=ax+b的图象上
∴解得a=2，b= -2
∴y= 2x-2
4
x
y
x
2
0
-1
N（-1，-4）
M（2，m）
（2）观察图象得：
当x<-1或0（2）根据图象写出反比例函数的值大于一次函数的值的x的取值范围。
连接ＯＭ，ＯＮ，求 ＭＯＮ的面积．
M
y
2
0
-1
N　
Ｆ
Ｅ
x
3、已知甲,乙两地相距skm,汽车从甲地匀速
行驶到乙地.如果汽车每小时耗油量为aL,那么从
甲地到乙地的总耗油量y(L)与汽车的行驶速度
v(km/h)的函数图象大致是( ).
o
(1) (2) (3) (4)
V(km/h)
Y/L
o
V(km/h)
Y/L
o
V(km/h)
Y/L
o
V(km/h)
Y/L
3
我思我进步5
耗油过程中的数学
某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（kPa）是气体体积V（m3）的反比例函数，其图象如图所示。当气球内的气压大于140 kPa时，气球将爆炸，为了安全起见，气体体积应（ ）
B
A、不大于
B、不小于
C、不大于 D、不小于
35
24
35
24
37
24
37
24
谈谈本节的学习你有哪些收 获和体会,你学会了哪些数学思想和解题方法
★深刻体会数形结合、分类讨论及转化等数学思想在反比例函数问题中的应用；
★熟练掌握和运用待定系数法求函数解析式和图形分割法求面积；
★深刻理解反比例函数中∣Ｋ∣的几何意义,通常应将反比例函数知识和几何知识联系起来解决问题。
例3、已知y=y1+y2, y1与x成正比
例,y2与x成反比例,并且当x=1
时,y=7;当x=4时,y=13.
(1)求y关于x的解析式,
(2)当x=-1时,求y的值.
小试 牛刀
学以致用
x
y
o
x
y
o
x
y
o
x
y
o
(1) (2) (3) (4)
(3) (2) (4) (1)
做 一 做
复习题(C)组
例2 已知一次函数 和反比例函数 （k≠0） 。
（1）k满足什么条件时这两个函数在同一坐标系xoy中图象有两个公共交点。
（2）设（1）中的两个公共点为A，B，则∠AOB是锐角还是钝角。
y
x
（1）∵两个函数在同一坐标系xoy中图象有两个公共交点。
∴有 有两个解
∴即方程 有两个解
∴△=36-4k>0 ∴K<9且k≠0
0O
A
B
K<0
A
B
（2）当 时∠AOB为锐角
当 时∠AOB为钝角