反比例应用

(共34张PPT)
小测：
1.若点（2，-4）在反比例函数 的图象上，则k=____.
2.若反比例函数 的图象在第二、四象限，则k的取值范围是____________.
3.反比例函数的图象既是______对称图形，又是 ______对称图形
4. 函数 的图象上有三点（－3,y1）, （－1,y2）, （2,y3）
则函数值y1、y2、y3的大小关系是_______________;
5.甲乙两地相距100km，一辆汽车从甲地开往乙地，
把汽车到达乙地所用的时间y(h)表示为汽车的平均
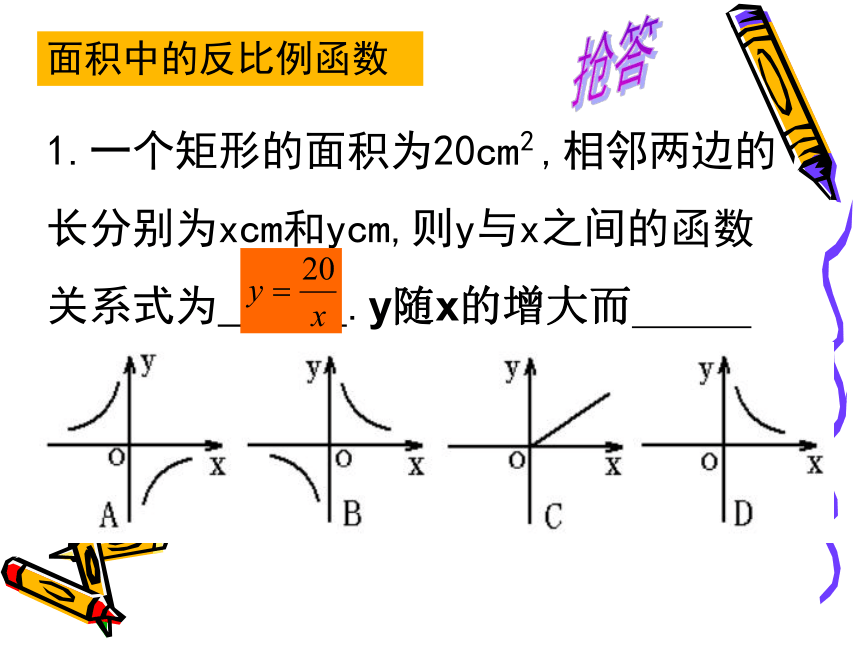
速度x(km/h)的函数，则这个函数的图象大致是（ ）
C
在实际问题中
图象就可能只
有一支.
K〈－1
-8
轴
中心
y3< y1< y2
学习目标：
1、会叙述反比例函数的主要性质，并能利用反比例函数的图象和性质解决一些实际问题。
2、提高观察、分析能力和对图形的感知水平。
3、进一步体会反比例函数刻画现实生活问题的作用。
1.一个矩形的面积为20cm ,相邻两边的长分别为xcm和ycm,则y与x之间的函数关系式为 .y随x的增大而
2
面积中的反比例函数
2.A、B两地间的高速公路长为300km,一辆汽车行完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的函数关系式为 .
行程中的反比例函数
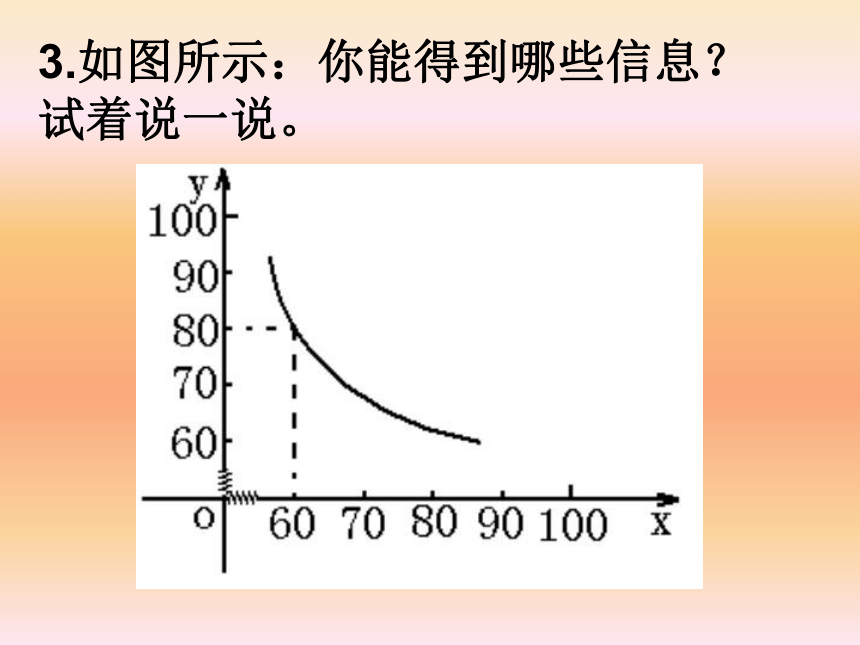
3.如图所示：你能得到哪些信息？
试着说一说。
某科技小组进行野外考察,途中遇到一片
十几米宽的烂泥湿地.为了安全迅速通过
这片湿地,他们沿着前进路线铺垫了若干
木板,构筑了一条临时通道,从而顺利完
成了任务.你能解释他们这样做的道理吗
当人和木板对湿地的压力一定时,随着木
板面积S(m2)的变化,人和木板对地面的
压强P(Pa)将如何变化
如果人和木板对湿地地面的压力合计600N,那么 (1)用含S的代数式表示P,P是S的反比例函数吗 为什么
P是S的反比例函数.
解:
(2)当木板面积为0.2m2时,压强是多少
解:当S=0.2m2时,P=600/0.2=3000(Pa)
某科技小组进行野外考察,途中遇到一片
十几米宽的烂泥湿地.为了安全迅速通过
这片湿地,他们沿着前进路线铺垫了若干
木板,构筑了一条临时通道,从而顺利完
成了任务.你能解释他们这样做的道理吗
当人和木板对湿地的压力一定时,随着木
板面积S(m2)的变化,人和木板对地面的
压强P(Pa)将如何变化
如果人和木板对湿地地面的压力合计600N,那么
如果人和木板对湿地地面的压力合计600N,那么
(3)如果要求压强不超过6000Pa,木板面积至少要多大
解:当P≤6000时,S≥600/6000=0.1(m2)
所以木板面积至少要0.1m2.
某科技小组进行野外考察,途中遇到一片
十几米宽的烂泥湿地.为了安全迅速通过
这片湿地,他们沿着前进路线铺垫了若干
木板,构筑了一条临时通道,从而顺利完
成了任务.你能解释他们这样做的道理吗
当人和木板对湿地的压力一定时,随着木
板面积S(m2)的变化,人和木板对地面的
压强P(Pa)将如何变化
某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗 当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化
如果人和木板对湿地地面的压力合计600N,那么
(4)在直角坐标系,作出相应函数的图象.
注意:只需在第一象限作出
函数的图象.因为S>0.
S … 0.1 0.2 0.3 0.4 0.6 …
… 6000 3000 2000 1500 1000 …
p=
S
600
(4)在直角坐标系,作出相应函数的图象
O
S/m
2
p/Pa
0.2
0.4
0.6
2000
4000
6000
只需在第一象限作函数的图象
(5)请利用图象对(2)和(3)作出直观解释,并与同伴交流.
解:问题(2)是已知图象上的某点的横坐标为0.2,求该点的纵坐标;问题(3)是已知图象上点的纵坐标不大于6000,求这些点所处位置及它们横坐标的取值范围.实际上这些点都在直线P=6000下方的图象上.
(2)当木板面积为0.2m2时,压强是多少
(3)如果要求压强不超过6000Pa,木板面积至少要多大
蓄电池的电压为定值.使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如图所示：
(1)此蓄电池的电压是 , 这一函数的表达式为 .
(2)当电流为18A时,用电器的电阻为 ;当电流为10A时,用电器的电阻为 .
(3)如果以此蓄电池为电源的用电器电流不得超过10A,那么用电器的可变电阻应控制在什么范围内
答：可变电阻应不小于3.6Ω.
36V
2Ω
3.6Ω
电学中的反比例函数
某蓄水池的排水管每小时排水8m3,6h可将满池水全部排空.
⑴此蓄水池的容积是_____.
⑵如果增加排水管.使每小时排水量达到
Q(m3),将满池水排空所需时间为t(h),t与Q之间的函数关系式为________.
⑶如果准备在5小时内将满池水排空，那么
每小时的排水量至少应为______.
⑷已知排水量最多为每小时12m3，则将满池水全部排空至少需要___h.
48m
3
9.6m
3
4
做一做
你能行！
2、某物体质量一定，若体积V=40m3，密度ρ=1.6kg/m3
（1）写出体积V与密度ρ的函数关系式。
（2）当密度ρ= 3.2kg/m3时，其体积为多少？
（3）若让该物体的体积控制在4m3~80m3之间，该物体的密度如何变化？
（1）分别写出这两个函数的表达式。
（2）你能求出点B的坐标吗？
你是怎样求的？
如图所示，正比例函数y=k1x的图象与反比例函数y= 的图象交于A、B两点，其中点A的坐标为（1,2）.
k2
x
如果反比例函数的图象与正比例函数的图象相交,一定有两个交点,这两个交点关于原点对称
(3)使反比例函数值大于正比例函数值的x的取值范围是 .
x＜-1或0＜x＜1
试一试
相信自己 ！
应用迁移,巩固提高
考点二:反比例函数与一次函数的综合运用.
例2.如图在Rt△AOB中,∠AOB=90°,点B在x轴上, 点A是直线y=x+m与双曲线 在第一象限的交点,且 S△AOB=3;求(1)m的值,(2)S△ACB的值.
y =
m
x
解:
O
x
y
A
B
(1)设A(x,y),则
S△AOB= OB AB= xy
1
2
.
1
2
∵xy=m,∴m/2=3,∴m=6.
∵∴∴∵∴∴
y=x+6
y =
6
x
y =
6
x
(2)直线y=x+6,双曲线 组成方程组
∴x1= - 3+ 15,
x1= - 3- 15 (不合题意) ,
∴y1= 3+ 15　∴A(- 3+ 15, 3+ 15)
.
∴S△ABC=1/2(BC AB)=12+3 15
应用迁移,巩固提高
考点二:反比例函数与一次函数的综合运用.
例4.(2004贵阳)如图,一次函数y=ax+b的图象与反比例函数 的图象交于M,N两点.
(1)求反比例函数和一次函数的解析式.
(2)根据图象写出使反比例函数的值大于
一次函数的值的x的取值范围.
y =
k
x
x
y
O
M(2,m)
N(-2,-4)
应用迁移,巩固提高
考点二:反比例函数与一次函数的综合运用.
例4.(2004贵阳)如图,一次函数y=ax+b的图象与反比例函数 的图象交于M,N两点.
(1)求反比例函数和一次函数的解析式.
(2)根据图象写出使反比例函数的值大于
一次函数的值的x的取值范围.
y =
k
x
x
y
O
M(2,m)
N(-2,-4)
解:
(1)点N(-1,- 4)在反比例函数的图象上,
∴ ∴k=4
∴反比例函数的解析式
-4 =
k
-1
y =
4
x
∵M(2,m)在反比例函数的图象上,
m =
4
2
∴ =2,
故点M(2,2)
将N(-1,- 4),M(2,2)代入y=ax+b中,
2a+b=2
-a+b= - 4
a=2
b= - 2
∴一次函数是y=2x-2
(2)由图象可知:
当x<-1,或0应用迁移,巩固提高
考点二:反比例函数与一次函数的综合运用.
例5.(成都)已知反比例函数 和一次函数y= - x – 6.(1)若一次函数和反比例函数的图象交于点( -3,m),求m和k的值.（2）若函数有两个交点，则k的取值范围(3)当k= -2时,设(2)中的两个函数图象的交点分别为A,B.试判断此时A,B两点分别在第几象限 ∠AOB是锐角还是钝角 (只要求写出结论).
(k ≠0)
y =
k
x
x
y
O
A
B
解:(1)
∵一次函数和反比例函数的图象都交于点(- 3,m)
∴
m=
-3
k
m=3- 6= -3
m= -3,k=9
(3)由题意可得: ,化简得x2+6x+k=0
要使两个函数的图象有两个不同的交点,必须使方程x2+6x+k=0有两个不相等的实数根,∴△=62 - 4k>0,解得k<9又k≠0∴当k<9且k≠0时,这两个函数的图象有两个不同的交点.
y=
x
k
y= - x - 6
A
y
O
B
x
M
N
A
y
O
B
x
M
N
C
D
A
y
O
B
x
M
N
C
D
勇攀高峰：为了预防“非典”，某学校对教室采用药熏消毒，已知药物燃烧时，室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后，y与x成反比例(如右图)，现测得药物8分钟燃毕，此时室内空气中每立方米的含药量6毫克，请根据题中所提供的信息，解答下列问题
(2)研究表明，当空气中每立方米的含药量低于1.6毫克时
学生方可进教室，那么从消毒开始，至少需要经过___分
钟后，学生才能回到教室
(3)研究表明，当空气中每立方米的含药量不低于3毫克且
持续时间不低于10分钟时，才能有效杀灭空气中的病菌，
那么此次消毒是否有效 为什么
(1)药物燃烧时，y关于x的函数关系式为 ,自变量x的取
值范围为 ；药物燃烧后，y关于x的函数关系式为 _.
3
检测：李先生参加了华联商厦推出的分期付款脑活动，他购买的电脑价格为1.2万元，交了首付款后每月付款y元，x个月结清余款，y与x的关系如图，试根据图像所提供的信息，回答下列问题
（1）确定y与x的关系式，并说明李先生多少首付款？
（2）李先生若用4个月结清
余款，每月应付多少元？
（3）如打算每月付款不
超过500元，李先生至
少几个月才能结清余款？
思考、某地上年度电价为每度电0.8元，年用电量
为1亿度，本年度计划将电价调至每度0.55---0.75
元之间，经测算，若电价调至每度x元，则本年度
新增用电量y（亿度）与(x-0.4)元成反比例，又当
x=0.65时，y=0.8.
⑴求y与x之间的函数关系式.
⑵若每度电的成本价为0.3元，则电价调至多少
元时，本年度电力部门的收益将比上年度增
加20%
能力训练
如图，Rt△ABO的顶点A是双曲线
与直线 y=-x+(k+1) 在第四象限的交点，AB⊥x 轴于B，且 .
(1)求这两个函数的表达式.
(2)求直线与双曲线的两个
交点A、C的坐标和△AOC
的面积.
五.能力训练
8.如图，已知反比例函数 的图象经过点
(2，3)，矩形ABCD的边BC在x轴上，E是对角线BD
的中点，函数 的图象又经过点两点A、E，
点E的横坐标为m. 解答下列问题：
(1)求k的值；
(2)求点C的坐标(用m表示)；
(3)当∠ABD=45°时，求m
的值.
说一说，你一定有新的启示
请你说一说本节课自己的收获并对自己参与学习的程度做出简单的评价.