北师大版九年级下册数学 3.4圆周角和圆心角的关系 同步习题(Word版 含解析)
文档属性
| 名称 | 北师大版九年级下册数学 3.4圆周角和圆心角的关系 同步习题(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 280.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览


文档简介
3.4圆周角和圆心角的关系 同步习题
一.选择题
1.如图,AB是⊙O的直径,弦CD交AB于点E,∠ACD=60°,∠ADC=40°,则∠CEB的度数为( )
A.110° B.115° C.120° D.105°
2.如图,AC为半圆的直径,弦AB=3,∠BAC=30°,点E、F分别为AB和AC上的动点,则BF+EF的最小值为( )
A. B. C.3 D.+
3.如图,点A、B、C在⊙O上,BC∥OA,连接BO并延长,交⊙O于点D,连接AC,DC.若∠A=25°,则∠D的大小为( )
A.25° B.30° C.40° D.50°
4.如图,AB是⊙O的直径,若∠BAC=20°,则∠ADC=( )
A.40° B.60° C.70° D.80°
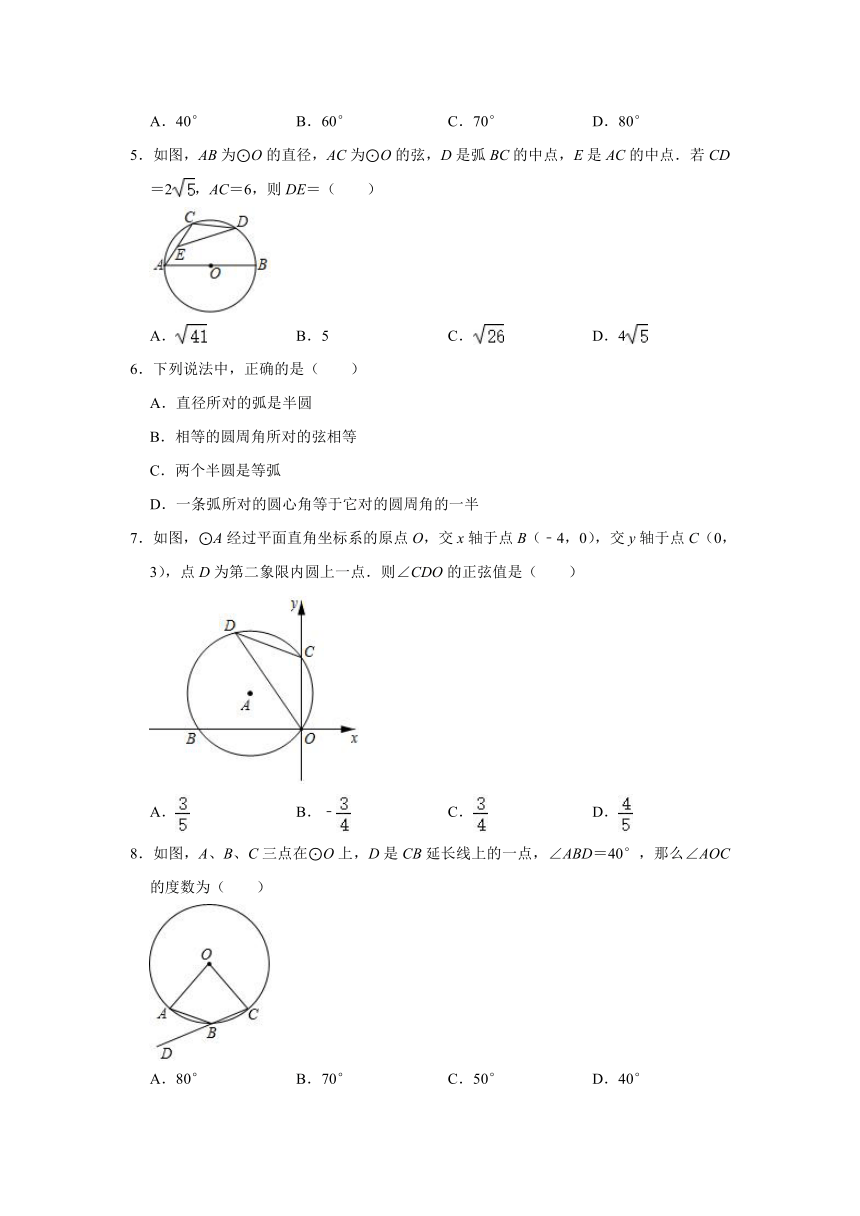
5.如图,AB为⊙O的直径,AC为⊙O的弦,D是弧BC的中点,E是AC的中点.若CD=2,AC=6,则DE=( )
A. B.5 C. D.4
6.下列说法中,正确的是( )
A.直径所对的弧是半圆
B.相等的圆周角所对的弦相等
C.两个半圆是等弧
D.一条弧所对的圆心角等于它对的圆周角的一半
7.如图,⊙A经过平面直角坐标系的原点O,交x轴于点B(﹣4,0),交y轴于点C(0,3),点D为第二象限内圆上一点.则∠CDO的正弦值是( )
A. B.﹣ C. D.
8.如图,A、B、C三点在⊙O上,D是CB延长线上的一点,∠ABD=40°,那么∠AOC的度数为( )
A.80° B.70° C.50° D.40°
9.如图,BC是⊙O的直径,点A、C1是圆上两点,连接AC、AB、AC1、BC1,若∠CBA=25°,则∠C1的度数为( )
A.85° B.75° C.65° D.55°
10.如图,正方形ABCD的边长为4,点E是BC上一点,以AB为直径在正方形内作半圆O,将△DCE沿DE翻折,点C刚好落在半圆O上的点F处,则CE的长为( )
A. B. C. D.
二.填空题
11.四边形ABCD是⊙O的内接四边形,∠A:∠C=4:1,则∠A= °.
12.如图,四边形ABCD是⊙O的内接四边形,对角线AC,BD交于点E,且AC=BD=AB,若∠AEB=70°,则∠AOB等于 °.
13.如图,四边形ABCD是⊙O的内接四边形,点E在边CD的延长线上,若∠ABC=110°,则∠ADE的度数为 .
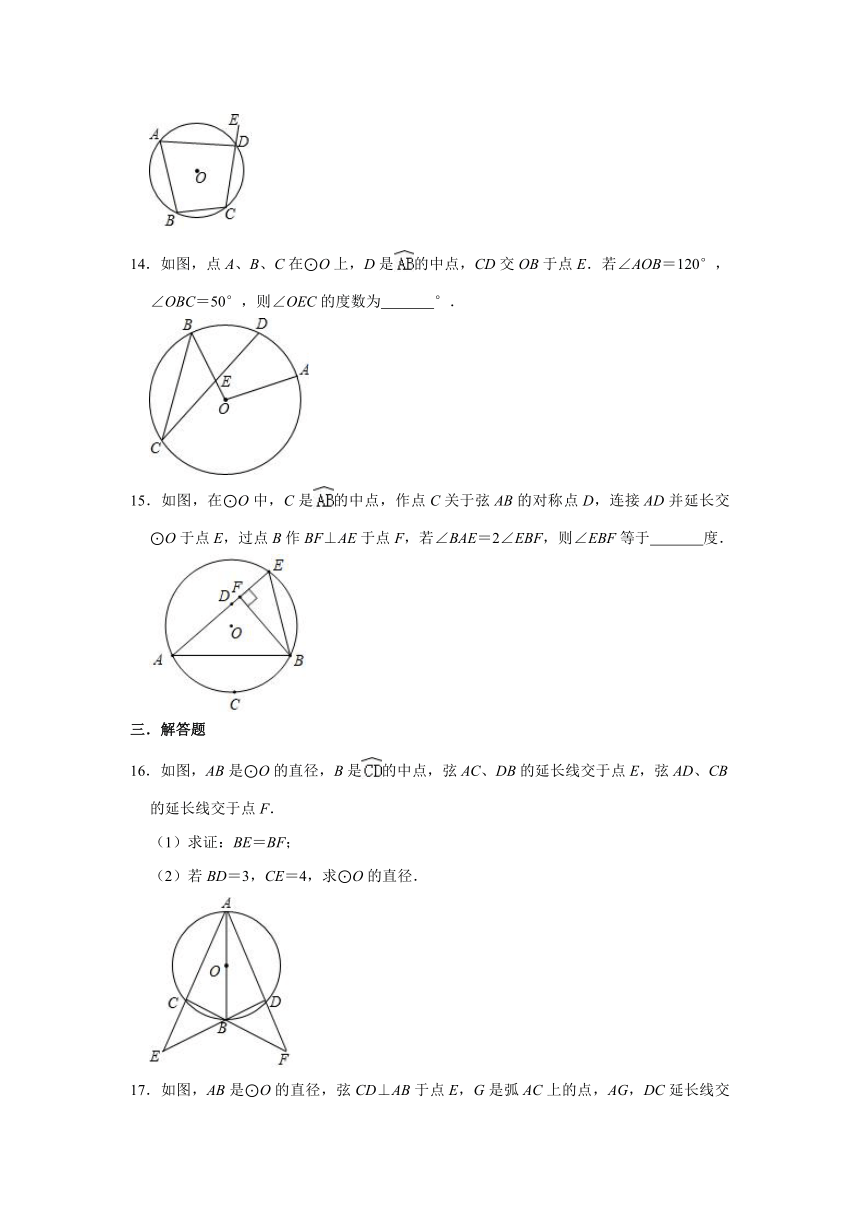
14.如图,点A、B、C在⊙O上,D是的中点,CD交OB于点E.若∠AOB=120°,∠OBC=50°,则∠OEC的度数为 °.
15.如图,在⊙O中,C是的中点,作点C关于弦AB的对称点D,连接AD并延长交⊙O于点E,过点B作BF⊥AE于点F,若∠BAE=2∠EBF,则∠EBF等于 度.
三.解答题
16.如图,AB是⊙O的直径,B是的中点,弦AC、DB的延长线交于点E,弦AD、CB的延长线交于点F.
(1)求证:BE=BF;
(2)若BD=3,CE=4,求⊙O的直径.
17.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上的点,AG,DC延长线交于点F.
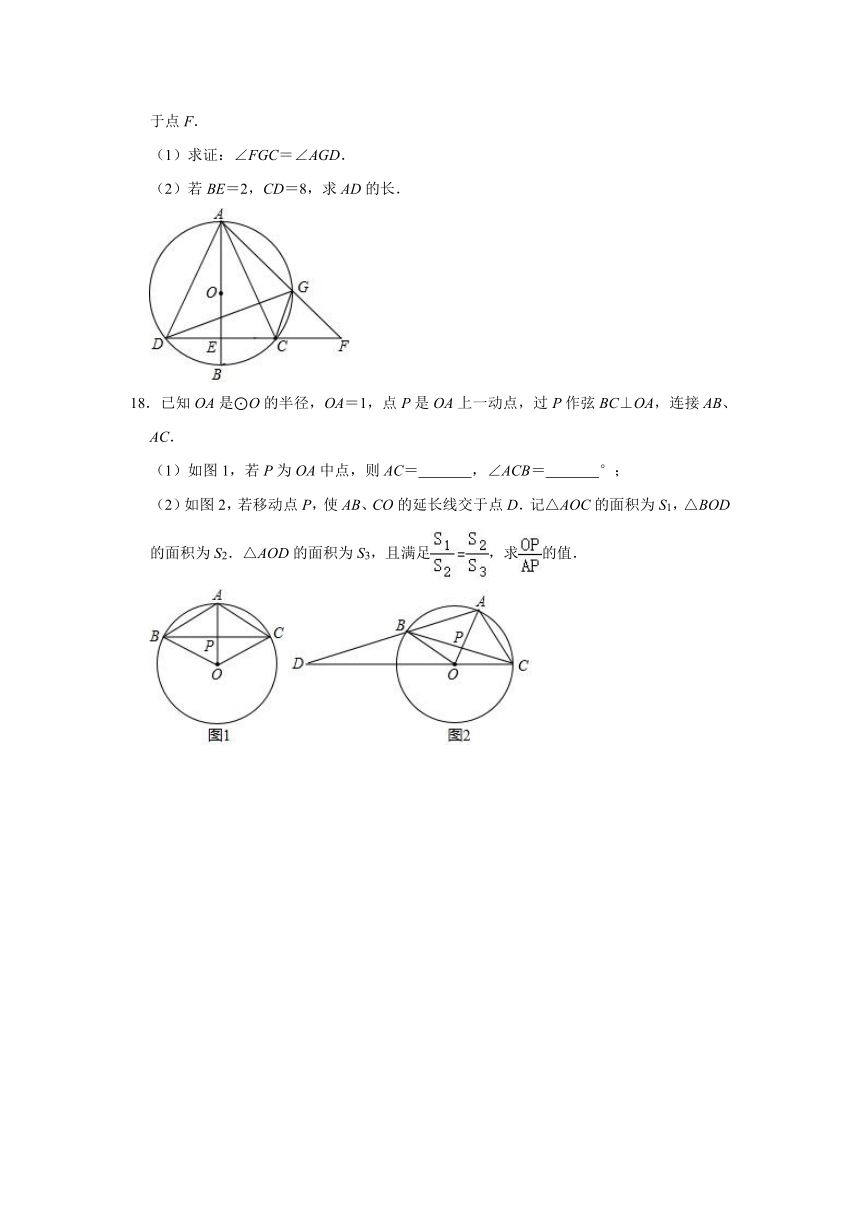
(1)求证:∠FGC=∠AGD.
(2)若BE=2,CD=8,求AD的长.
18.已知OA是⊙O的半径,OA=1,点P是OA上一动点,过P作弦BC⊥OA,连接AB、AC.
(1)如图1,若P为OA中点,则AC= ,∠ACB= °;
(2)如图2,若移动点P,使AB、CO的延长线交于点D.记△AOC的面积为S1,△BOD的面积为S2.△AOD的面积为S3,且满足,求的值.
参考答案
一.选择题
1.解:连接BC.
∴∠ADC=∠B,
∵∠ADC=40°,
∴∠B=40°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=50°,
∵∠CEB=∠ACD+∠BAC,∠ACD=60°,
∴∠CEB=60°+50°=110°.
故选:A.
2.解:作B点关于直径AC的对称点B′,过B′点作B′E⊥AB于E,交AC于F,如图,
则FB=FB′,
∴FB+FE=FB′+FE=B′E,
此时FB+FE的值最小,
∵∠BAC=30°,
∴∠B′AC=30°,
∴∠BAB′=60°,
∵AB=AB′,
∴△ABB′为等边三角形,
∵B′E⊥AB,
∴AE=BE=,
∴B′E=AE=,
即BF+EF的最小值为.
故选:B.
3.解:∵BC∥OA,
∴∠ACB=∠A=25°,∠B=∠AOB=2∠ACB=50°,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠D=90°﹣∠B=90°﹣50°=40°,
故选:C.
4.解:∵AB是直径,
∴∠ACB=90°,
∵∠BAC=20°,
∴∠ABC=90°﹣20°=70°,
∴∠ADC=∠ABC=70°,
故选:C.
5.解:连接OC、BC、OE、BD,OE交⊙O于F,OD交BC于G,如图,
∵D是弧BC的中点,
∴OD⊥BC,CG=BG,DB=DC=2,∠BOD=∠COD,
∵E是AC的中点,
∴OE⊥AC,=,
∴∠AOF=∠COF,
∴∠DOF=×180°=90°,
∵OA=OB,BG=CG,
∴OG∥AC,OG=AC=3,
设⊙O的半径为r,则DG=r﹣3,
在Rt△OBG中,BG2=r2﹣32,
在Rt△DBG中,BG2=(2)2﹣(r﹣3)2,
∴r2﹣32=(2)2﹣(r﹣3)2,解得r1=﹣2(舍去),r2=5,
∴OD=5,
∴BG==4,
易得四边形OGCE为矩形,
∴OE=CG=BG=4,
在Rt△DOE中,DE==.
故选:A.
6.解:A、直径所对的弧是半圆,正确,符合题意;
B、同圆或等圆中,相等的圆周角所对的弦相等,故原命题错误,不符合题意;
C、半径相等的两个半圆是等弧,故原命题错误,不符合题意;
D、同圆或等圆中,一条弧所对的圆心角等于它对的圆周角的一半,故原命题错误,不符合题意,
故选:A.
7.解:连接BC,如图,
∵B(﹣4,0),C(0,3),
∴OB=4,OC=3,
∴BC==5,
∴sin∠OBC==,
∵∠ODC=∠OBC,
∴sin∠CDO=sin∠OBC=.
故选:A.
8.解:所对的圆周角∠AEC,如图,
∵∠ABD=40°,
∴∠ABC=180°﹣40°=140°,
∵∠AEC+∠ABC=180°,
∴∠E=40°,
∴∠AOC=2∠AEC=2×40°=80°.
故选:A.
9.解:∵BC是⊙O的直径,
∴∠BAC=90°,
∵∠CBA=25°,
∴∠C=90°﹣∠CBA=65°,
∴∠C1=∠C=65°;
故选:C.
10.解:连接DO,OF,
∵四边形ABCD是正方形,将△DCE沿DE翻折得到△DFE,
∴DC=DA,DC=DF,
∴DA=DF,
在△DAO和△DFO中,
,
∴△DAO≌△DFO(SSS),
∴∠A=∠DFO,
∵∠A=90°,
∴∠DFO=90°,
又∵∠DFE=∠C=90°,
∴∠DFO=∠DFE,
∴点O、F、E三点共线,
设CE=x,则OE=OF+EF=2+x,BE=4﹣x,OB=2,
∵∠OBE=90°,
∴22+(4﹣x)2=(2+x)2,
解得,x=,
即CE的长为,
故选:B.
二.填空题
11.解:
设∠A=4x°,∠C=x°,
∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,
∴4x+x=180,
解得:x=36,
即∠A=144°,
故答案为:144.
12.解:延长AO交BC于点G,延长BO交AD于点H,
∵AC=AB,
∴=,
∴AG⊥BC,BG=CG,
∴∠CAO=∠BAO,
∵BD=AB,
∴=,
∴BH⊥AD,AH=DH,
∴∠ABO=∠DBO,
∵∠AEB=70°,
∴∠ABO+∠OAB=(∠EAB+∠EBA)=(180°﹣70°)=55°,
∴∠AOB=180°﹣55°=125°.
故答案为:125.
13.解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADE=∠ABC=110°,
故答案为:110°.
14.解:连接OD,
∵D是的中点,∠AOB=120°,
∴∠BOD=∠AOD=∠AOB=60°,
由圆周角定理得,∠BCD=∠BOD=30°,
∴∠OEC=∠BCD+∠OBC=80°,
故答案为:80.
15.解:设∠EBF=x,则∠BAE=2x,
∴BF⊥AE,
∴∠E=90°﹣x,
∵C点和D点关于AB对称,
∴AD=AC,AB垂直平分CD,
∴AB平分∠CAD,
∴∠CAB=∠DAB=2x,
∵C是的中点,
∴∠ABC=∠CAB=2x,
∴∠ACB=180°﹣4x,
∵∠ACB+∠AEB=180°,
∴180°﹣4x+90°﹣x=180°,解得x=18°,
即∠EBF等于18度.
故答案为18.
三.解答题
16.(1)证明:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵B是的中点,
∴=,
∴BC=BD,
在△BCE和△BDF中
,
∴△BCE≌△BDF(ASA),
∴BE=BF;
(2)解:∵BC=BD=3,
而CE=4,
∴BE===5,
∵AC=,AD=,
而BC=BD,
∴AC=AD,
设AC=AD=x,
在Rt△ADE中,x2+82=(x+4)2,解得x=6,
即AC=6,
在Rt△ACB中,AB==3,
即⊙O的直径为3.
17.(1)证明:∵弦CD⊥AB,
∴,
∴∠AGD=∠ADC,
∵四边形ABCG是圆内接四边形,
∴∠FGC=∠ADC,
∴∠FGC=∠AGD;
(2)解:连接OD,如图,
∵CD⊥AB,CD=8
∴DE=CE=4,
在Rt△DOE中,∵DO2=OE2+ED2,
∴DO2=(OD﹣2)2+42,解得OD=5,
∴AE=10﹣2=8,
∴AD=.
18.解:(1)∵P为OA的中点,OA⊥BC,
∴AC=OA,
∵OC=OA,
∴OC=OA=AC,
∴△AOC为等边三角形,
∴AC=1,∠ACO=60°,
∵PC⊥OA,
∴∠ACB=∠BCO=∠AOC=30°,
故答案为:1;30.
(2)若DC与圆O相交于点E,连接BE,
∵BC⊥OA,
∴PB=PC,
∴AB=AC,
∵OB=CO,OA=OA,
∴△ABO≌△ACO(SSS),
∴S△ABO=S△ACO=S1,
∴S1+S2=S3,
∵,
∴,
∴S12+S1S2﹣S22=0,
∴﹣1=0.
解得:,
∴,
∴,
∴,
∵CE为直径,
∴∠CBE=90°,
∴AO∥BE,
∴△AOD∽△BED,
∴,
∵OE=OC,
∴OP=BE,
∴,
∴+1,
∴,
∴.
一.选择题
1.如图,AB是⊙O的直径,弦CD交AB于点E,∠ACD=60°,∠ADC=40°,则∠CEB的度数为( )
A.110° B.115° C.120° D.105°
2.如图,AC为半圆的直径,弦AB=3,∠BAC=30°,点E、F分别为AB和AC上的动点,则BF+EF的最小值为( )
A. B. C.3 D.+
3.如图,点A、B、C在⊙O上,BC∥OA,连接BO并延长,交⊙O于点D,连接AC,DC.若∠A=25°,则∠D的大小为( )
A.25° B.30° C.40° D.50°
4.如图,AB是⊙O的直径,若∠BAC=20°,则∠ADC=( )
A.40° B.60° C.70° D.80°
5.如图,AB为⊙O的直径,AC为⊙O的弦,D是弧BC的中点,E是AC的中点.若CD=2,AC=6,则DE=( )
A. B.5 C. D.4
6.下列说法中,正确的是( )
A.直径所对的弧是半圆
B.相等的圆周角所对的弦相等
C.两个半圆是等弧
D.一条弧所对的圆心角等于它对的圆周角的一半
7.如图,⊙A经过平面直角坐标系的原点O,交x轴于点B(﹣4,0),交y轴于点C(0,3),点D为第二象限内圆上一点.则∠CDO的正弦值是( )
A. B.﹣ C. D.
8.如图,A、B、C三点在⊙O上,D是CB延长线上的一点,∠ABD=40°,那么∠AOC的度数为( )
A.80° B.70° C.50° D.40°
9.如图,BC是⊙O的直径,点A、C1是圆上两点,连接AC、AB、AC1、BC1,若∠CBA=25°,则∠C1的度数为( )
A.85° B.75° C.65° D.55°
10.如图,正方形ABCD的边长为4,点E是BC上一点,以AB为直径在正方形内作半圆O,将△DCE沿DE翻折,点C刚好落在半圆O上的点F处,则CE的长为( )
A. B. C. D.
二.填空题
11.四边形ABCD是⊙O的内接四边形,∠A:∠C=4:1,则∠A= °.
12.如图,四边形ABCD是⊙O的内接四边形,对角线AC,BD交于点E,且AC=BD=AB,若∠AEB=70°,则∠AOB等于 °.
13.如图,四边形ABCD是⊙O的内接四边形,点E在边CD的延长线上,若∠ABC=110°,则∠ADE的度数为 .
14.如图,点A、B、C在⊙O上,D是的中点,CD交OB于点E.若∠AOB=120°,∠OBC=50°,则∠OEC的度数为 °.
15.如图,在⊙O中,C是的中点,作点C关于弦AB的对称点D,连接AD并延长交⊙O于点E,过点B作BF⊥AE于点F,若∠BAE=2∠EBF,则∠EBF等于 度.
三.解答题
16.如图,AB是⊙O的直径,B是的中点,弦AC、DB的延长线交于点E,弦AD、CB的延长线交于点F.
(1)求证:BE=BF;
(2)若BD=3,CE=4,求⊙O的直径.
17.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上的点,AG,DC延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)若BE=2,CD=8,求AD的长.
18.已知OA是⊙O的半径,OA=1,点P是OA上一动点,过P作弦BC⊥OA,连接AB、AC.
(1)如图1,若P为OA中点,则AC= ,∠ACB= °;
(2)如图2,若移动点P,使AB、CO的延长线交于点D.记△AOC的面积为S1,△BOD的面积为S2.△AOD的面积为S3,且满足,求的值.
参考答案
一.选择题
1.解:连接BC.
∴∠ADC=∠B,
∵∠ADC=40°,
∴∠B=40°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=50°,
∵∠CEB=∠ACD+∠BAC,∠ACD=60°,
∴∠CEB=60°+50°=110°.
故选:A.
2.解:作B点关于直径AC的对称点B′,过B′点作B′E⊥AB于E,交AC于F,如图,
则FB=FB′,
∴FB+FE=FB′+FE=B′E,
此时FB+FE的值最小,
∵∠BAC=30°,
∴∠B′AC=30°,
∴∠BAB′=60°,
∵AB=AB′,
∴△ABB′为等边三角形,
∵B′E⊥AB,
∴AE=BE=,
∴B′E=AE=,
即BF+EF的最小值为.
故选:B.
3.解:∵BC∥OA,
∴∠ACB=∠A=25°,∠B=∠AOB=2∠ACB=50°,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠D=90°﹣∠B=90°﹣50°=40°,
故选:C.
4.解:∵AB是直径,
∴∠ACB=90°,
∵∠BAC=20°,
∴∠ABC=90°﹣20°=70°,
∴∠ADC=∠ABC=70°,
故选:C.
5.解:连接OC、BC、OE、BD,OE交⊙O于F,OD交BC于G,如图,
∵D是弧BC的中点,
∴OD⊥BC,CG=BG,DB=DC=2,∠BOD=∠COD,
∵E是AC的中点,
∴OE⊥AC,=,
∴∠AOF=∠COF,
∴∠DOF=×180°=90°,
∵OA=OB,BG=CG,
∴OG∥AC,OG=AC=3,
设⊙O的半径为r,则DG=r﹣3,
在Rt△OBG中,BG2=r2﹣32,
在Rt△DBG中,BG2=(2)2﹣(r﹣3)2,
∴r2﹣32=(2)2﹣(r﹣3)2,解得r1=﹣2(舍去),r2=5,
∴OD=5,
∴BG==4,
易得四边形OGCE为矩形,
∴OE=CG=BG=4,
在Rt△DOE中,DE==.
故选:A.
6.解:A、直径所对的弧是半圆,正确,符合题意;
B、同圆或等圆中,相等的圆周角所对的弦相等,故原命题错误,不符合题意;
C、半径相等的两个半圆是等弧,故原命题错误,不符合题意;
D、同圆或等圆中,一条弧所对的圆心角等于它对的圆周角的一半,故原命题错误,不符合题意,
故选:A.
7.解:连接BC,如图,
∵B(﹣4,0),C(0,3),
∴OB=4,OC=3,
∴BC==5,
∴sin∠OBC==,
∵∠ODC=∠OBC,
∴sin∠CDO=sin∠OBC=.
故选:A.
8.解:所对的圆周角∠AEC,如图,
∵∠ABD=40°,
∴∠ABC=180°﹣40°=140°,
∵∠AEC+∠ABC=180°,
∴∠E=40°,
∴∠AOC=2∠AEC=2×40°=80°.
故选:A.
9.解:∵BC是⊙O的直径,
∴∠BAC=90°,
∵∠CBA=25°,
∴∠C=90°﹣∠CBA=65°,
∴∠C1=∠C=65°;
故选:C.
10.解:连接DO,OF,
∵四边形ABCD是正方形,将△DCE沿DE翻折得到△DFE,
∴DC=DA,DC=DF,
∴DA=DF,
在△DAO和△DFO中,
,
∴△DAO≌△DFO(SSS),
∴∠A=∠DFO,
∵∠A=90°,
∴∠DFO=90°,
又∵∠DFE=∠C=90°,
∴∠DFO=∠DFE,
∴点O、F、E三点共线,
设CE=x,则OE=OF+EF=2+x,BE=4﹣x,OB=2,
∵∠OBE=90°,
∴22+(4﹣x)2=(2+x)2,
解得,x=,
即CE的长为,
故选:B.
二.填空题
11.解:
设∠A=4x°,∠C=x°,
∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,
∴4x+x=180,
解得:x=36,
即∠A=144°,
故答案为:144.
12.解:延长AO交BC于点G,延长BO交AD于点H,
∵AC=AB,
∴=,
∴AG⊥BC,BG=CG,
∴∠CAO=∠BAO,
∵BD=AB,
∴=,
∴BH⊥AD,AH=DH,
∴∠ABO=∠DBO,
∵∠AEB=70°,
∴∠ABO+∠OAB=(∠EAB+∠EBA)=(180°﹣70°)=55°,
∴∠AOB=180°﹣55°=125°.
故答案为:125.
13.解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADE=∠ABC=110°,
故答案为:110°.
14.解:连接OD,
∵D是的中点,∠AOB=120°,
∴∠BOD=∠AOD=∠AOB=60°,
由圆周角定理得,∠BCD=∠BOD=30°,
∴∠OEC=∠BCD+∠OBC=80°,
故答案为:80.
15.解:设∠EBF=x,则∠BAE=2x,
∴BF⊥AE,
∴∠E=90°﹣x,
∵C点和D点关于AB对称,
∴AD=AC,AB垂直平分CD,
∴AB平分∠CAD,
∴∠CAB=∠DAB=2x,
∵C是的中点,
∴∠ABC=∠CAB=2x,
∴∠ACB=180°﹣4x,
∵∠ACB+∠AEB=180°,
∴180°﹣4x+90°﹣x=180°,解得x=18°,
即∠EBF等于18度.
故答案为18.
三.解答题
16.(1)证明:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵B是的中点,
∴=,
∴BC=BD,
在△BCE和△BDF中
,
∴△BCE≌△BDF(ASA),
∴BE=BF;
(2)解:∵BC=BD=3,
而CE=4,
∴BE===5,
∵AC=,AD=,
而BC=BD,
∴AC=AD,
设AC=AD=x,
在Rt△ADE中,x2+82=(x+4)2,解得x=6,
即AC=6,
在Rt△ACB中,AB==3,
即⊙O的直径为3.
17.(1)证明:∵弦CD⊥AB,
∴,
∴∠AGD=∠ADC,
∵四边形ABCG是圆内接四边形,
∴∠FGC=∠ADC,
∴∠FGC=∠AGD;
(2)解:连接OD,如图,
∵CD⊥AB,CD=8
∴DE=CE=4,
在Rt△DOE中,∵DO2=OE2+ED2,
∴DO2=(OD﹣2)2+42,解得OD=5,
∴AE=10﹣2=8,
∴AD=.
18.解:(1)∵P为OA的中点,OA⊥BC,
∴AC=OA,
∵OC=OA,
∴OC=OA=AC,
∴△AOC为等边三角形,
∴AC=1,∠ACO=60°,
∵PC⊥OA,
∴∠ACB=∠BCO=∠AOC=30°,
故答案为:1;30.
(2)若DC与圆O相交于点E,连接BE,
∵BC⊥OA,
∴PB=PC,
∴AB=AC,
∵OB=CO,OA=OA,
∴△ABO≌△ACO(SSS),
∴S△ABO=S△ACO=S1,
∴S1+S2=S3,
∵,
∴,
∴S12+S1S2﹣S22=0,
∴﹣1=0.
解得:,
∴,
∴,
∴,
∵CE为直径,
∴∠CBE=90°,
∴AO∥BE,
∴△AOD∽△BED,
∴,
∵OE=OC,
∴OP=BE,
∴,
∴+1,
∴,
∴.
