湘教版九年级数学上册第3章图形的相似-单元测试(word版含答案)
文档属性
| 名称 | 湘教版九年级数学上册第3章图形的相似-单元测试(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 253.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览

文档简介
南强中学2020年九年级上册《图形的相似》单元测试题
一、选择题(共8小题,每小题3分,共24分)
1、在比例尺为1:5000的地图上,量得甲,乙两地的距离25cm,则甲,乙的实际距离是(
)
A.1250km
B.125km
C.
12.5km
D.1.25km
2、已知,则的值为(
)
A.
B.
C.2
D.
3、已知⊿ABC的三边长分别为,,2,⊿A′B′C′的两边长分别是1和,如果⊿ABC与⊿A′B′C′相似,那么⊿A′B′C′的第三边长应该是(
)
A.
B.
C.
D.
4、在相同时刻,物高与影长成正比。如果高为1.5米的标杆影长为2.5米,那么影长为30米的旗杆的高为(
)
A
20米
B
18米
C
16米
D
15米
5、如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC∽⊿CAD,只要CD等于
(
)
A.
B.
C.
D.
6、如图,□ABCD中,EF∥AB,DE∶EA
=
2∶3,EF
=
4,则CD的长(
)
A.
B.8
C.10
D.16
7、如图,一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角,窗户的高在教室地面上的影长MN=米,窗户的下檐到教室地面的距离BC=1米(点M、N、C在同一直线上),则窗户的高AB为
(
)
A.米 B.米 C.2米 D.1.5米
8、如图,将△ABC的高AD四等分,过每一个分点作底边的平行线,把三角形的面积分成四部分S1、S2、S3、S4,则S1︰S2︰S3︰S4等于( )
(A)1︰2︰3︰4 (B)2︰3︰4︰5 (C)1︰3︰5︰7 (D)3︰5︰7︰9
第5题图
第6题图
第7题图
二、填空题(共8小题,每小题3分,共24分)
9、已知,则
10、已知点C是线段AB的黄金分割点,且AC>BC,则AC∶AB=
.
11、如果x︰y︰z=1︰3︰5,那么=___________.
第12题
12、如图,小伟在打网球时,击球点距离球网的水平距离是8米,已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击球的高度h为
米.
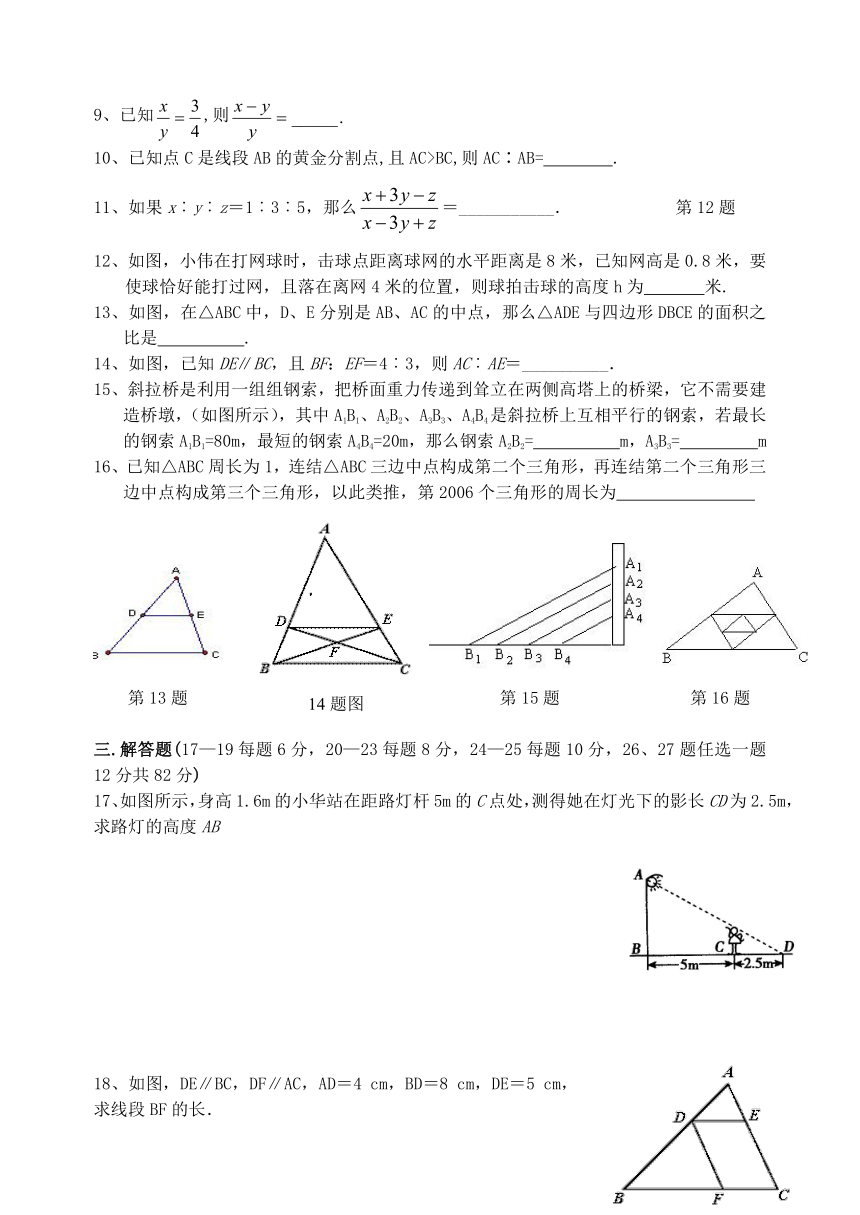
13、如图,在△ABC中,D、E分别是AB、AC的中点,那么△ADE与四边形DBCE的面积之比是
.
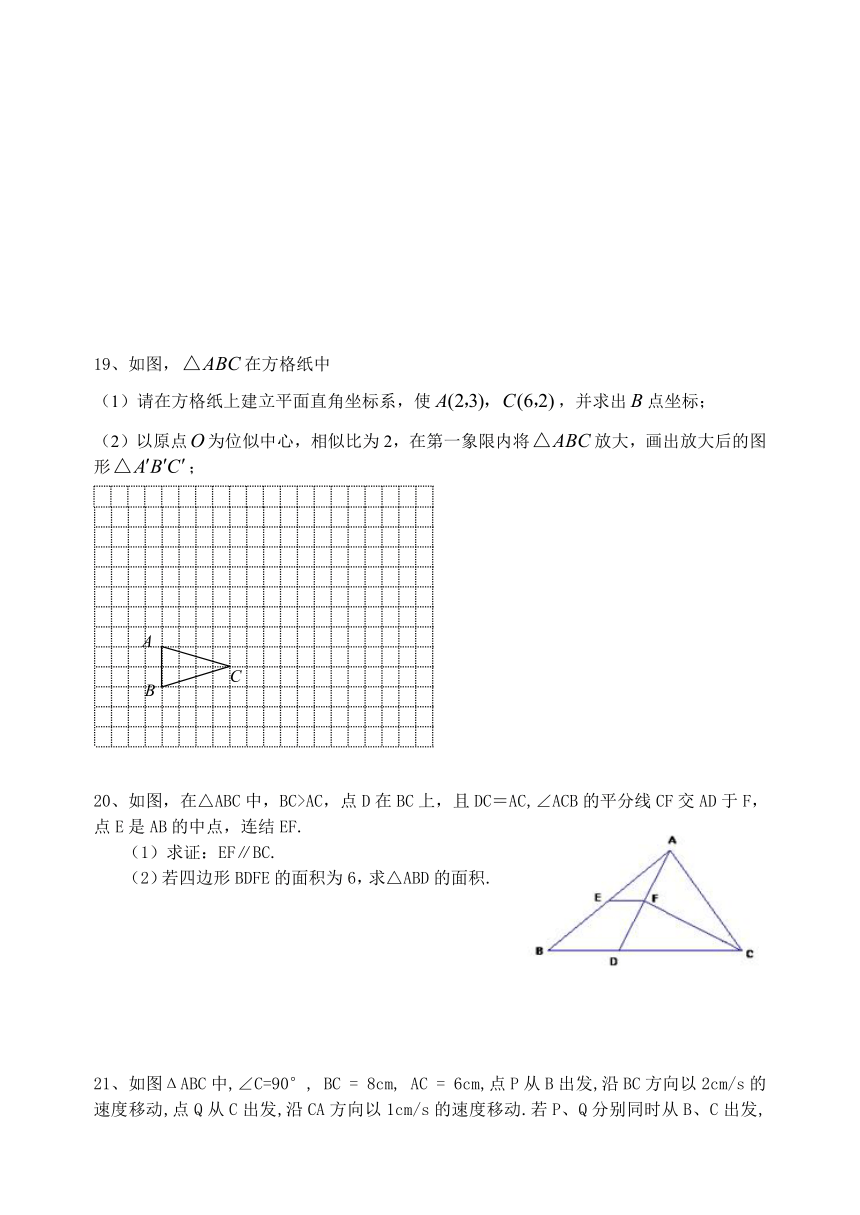
14、如图,已知DE∥BC,且BF:EF=4︰3,则AC︰AE=__________.
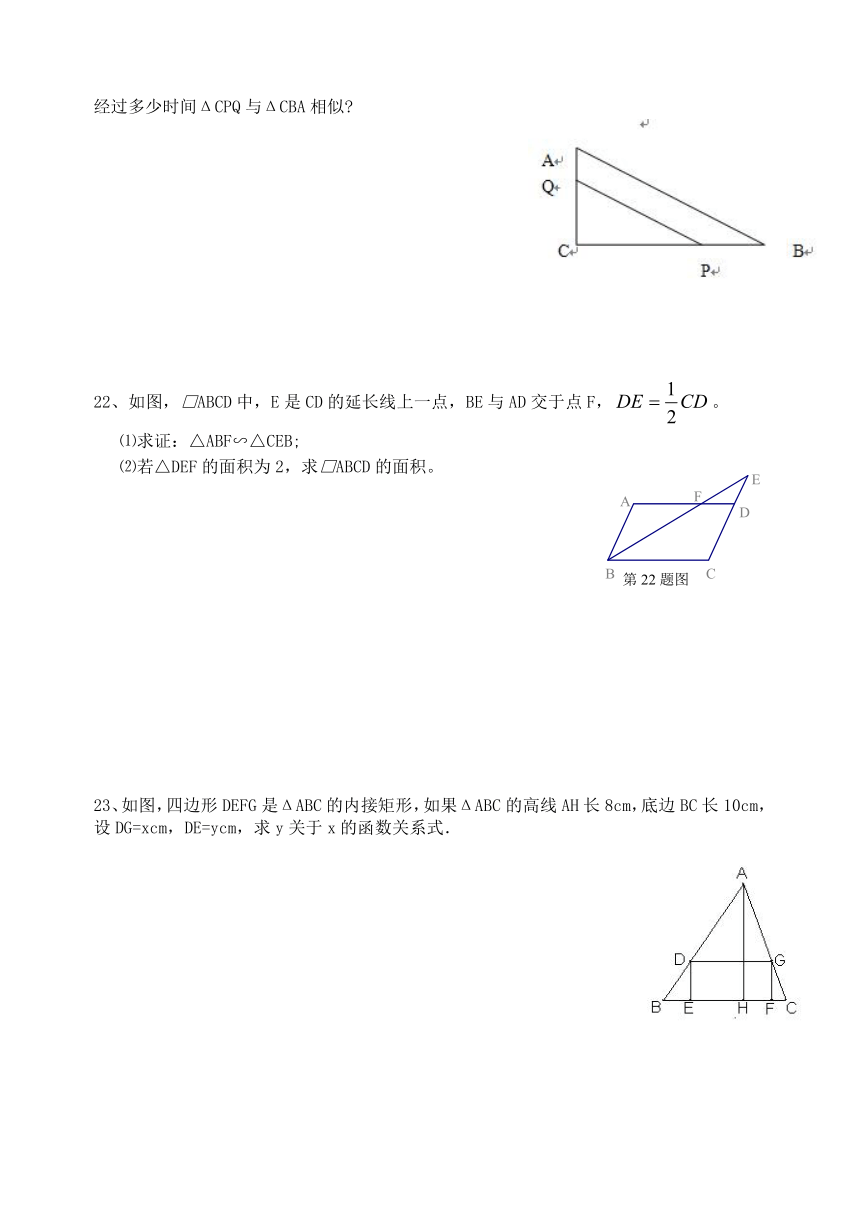
15、斜拉桥是利用一组组钢索,把桥面重力传递到耸立在两侧高塔上的桥梁,它不需要建造桥墩,(如图所示),其中A1B1、A2B2、A3B3、A4B4是斜拉桥上互相平行的钢索,若最长的钢索A1B1=80m,最短的钢索A4B4=20m,那么钢索A2B2=
m,A3B3=
m
16、已知△ABC周长为1,连结△ABC三边中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,以此类推,第2006个三角形的周长为
第13题
第15题
第16题
三.解答题(17—19每题6分,20—23每题8分,24—25每题10分,26、27题任选一题12分共82分)
17、如图所示,身高1.6m的小华站在距路灯杆5m的C点处,测得她在灯光下的影长CD为2.5m,求路灯的高度AB
18、如图,DE∥BC,DF∥AC,AD=4
cm,BD=8
cm,DE=5
cm,求线段BF的长.
19、如图,在方格纸中
(1)请在方格纸上建立平面直角坐标系,使,并求出点坐标;
(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;
20、如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF.
(1)求证:EF∥BC.
(2)若四边形BDFE的面积为6,求△ABD的面积.
21、如图ΔABC中,∠C=90°,
BC
=
8cm,
AC
=
6cm,点P从B出发,沿BC方向以2cm/s的速度移动,点Q从C出发,沿CA方向以1cm/s的速度移动.若P、Q分别同时从B、C出发,经过多少时间ΔCPQ与ΔCBA相似?
22、如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,。
⑴求证:△ABF∽△CEB;
⑵若△DEF的面积为2,求□ABCD的面积。
23、如图,四边形DEFG是ΔABC的内接矩形,如果ΔABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,求y关于x的函数关系式.
24、如图,梯形ABCD中.AB∥CD.且AB=2CD,E,F分别是AB,BC的中点。EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
25、如图,
等边⊿ABC,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明⊿ABD≌⊿BCE.
(2)⊿AEF与⊿ABE相似吗?说说你的理由.
(3)BD2=AD·DF吗?请说明理由.
26、如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.
27、如图所示在△OAB中,O为坐标原点,横、纵轴的单位长度相同,A、B的坐标分别为(8,6),(16,0),点P沿OA边从点O开始向终点A运动,速度每秒1个单位,点Q沿BO边从B点开始向终点O运动,速度每秒2个单位,如果P、Q同时出发,用t(秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动。
求(1)几秒时PQ∥AB
(2)设△OPQ的面积为y,求y与t的函数关系式.
(3)△OPQ与△OAB能否相似,若能,求出点P的坐标,若不能,试说明理由
南强中学2020年九年级上册《图形的相似》单元测试题答案
一、选择题:1.D;
2.
B;
3.A;
4.B;
5.A;6.
C;7.C;8.C
二、填空题:9.
10.
11.
;
12.
2.4;
13.
;
14.
4:3
15.
60
40;
16.
三、解答题:
17.有题意可得
解得
18.
有题意可得即
解得
19.(1)B(2.1)
(2)略
20.(1),
①时,解得=S
②时,解得=S
(1)略
(1),
(2)
25.
(1)SAS证明
(2)通过证明
证明
(3)
一、选择题(共8小题,每小题3分,共24分)
1、在比例尺为1:5000的地图上,量得甲,乙两地的距离25cm,则甲,乙的实际距离是(
)
A.1250km
B.125km
C.
12.5km
D.1.25km
2、已知,则的值为(
)
A.
B.
C.2
D.
3、已知⊿ABC的三边长分别为,,2,⊿A′B′C′的两边长分别是1和,如果⊿ABC与⊿A′B′C′相似,那么⊿A′B′C′的第三边长应该是(
)
A.
B.
C.
D.
4、在相同时刻,物高与影长成正比。如果高为1.5米的标杆影长为2.5米,那么影长为30米的旗杆的高为(
)
A
20米
B
18米
C
16米
D
15米
5、如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC∽⊿CAD,只要CD等于
(
)
A.
B.
C.
D.
6、如图,□ABCD中,EF∥AB,DE∶EA
=
2∶3,EF
=
4,则CD的长(
)
A.
B.8
C.10
D.16
7、如图,一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角,窗户的高在教室地面上的影长MN=米,窗户的下檐到教室地面的距离BC=1米(点M、N、C在同一直线上),则窗户的高AB为
(
)
A.米 B.米 C.2米 D.1.5米
8、如图,将△ABC的高AD四等分,过每一个分点作底边的平行线,把三角形的面积分成四部分S1、S2、S3、S4,则S1︰S2︰S3︰S4等于( )
(A)1︰2︰3︰4 (B)2︰3︰4︰5 (C)1︰3︰5︰7 (D)3︰5︰7︰9
第5题图
第6题图
第7题图
二、填空题(共8小题,每小题3分,共24分)
9、已知,则
10、已知点C是线段AB的黄金分割点,且AC>BC,则AC∶AB=
.
11、如果x︰y︰z=1︰3︰5,那么=___________.
第12题
12、如图,小伟在打网球时,击球点距离球网的水平距离是8米,已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击球的高度h为
米.
13、如图,在△ABC中,D、E分别是AB、AC的中点,那么△ADE与四边形DBCE的面积之比是
.
14、如图,已知DE∥BC,且BF:EF=4︰3,则AC︰AE=__________.
15、斜拉桥是利用一组组钢索,把桥面重力传递到耸立在两侧高塔上的桥梁,它不需要建造桥墩,(如图所示),其中A1B1、A2B2、A3B3、A4B4是斜拉桥上互相平行的钢索,若最长的钢索A1B1=80m,最短的钢索A4B4=20m,那么钢索A2B2=
m,A3B3=
m
16、已知△ABC周长为1,连结△ABC三边中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,以此类推,第2006个三角形的周长为
第13题
第15题
第16题
三.解答题(17—19每题6分,20—23每题8分,24—25每题10分,26、27题任选一题12分共82分)
17、如图所示,身高1.6m的小华站在距路灯杆5m的C点处,测得她在灯光下的影长CD为2.5m,求路灯的高度AB
18、如图,DE∥BC,DF∥AC,AD=4
cm,BD=8
cm,DE=5
cm,求线段BF的长.
19、如图,在方格纸中
(1)请在方格纸上建立平面直角坐标系,使,并求出点坐标;
(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;
20、如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF.
(1)求证:EF∥BC.
(2)若四边形BDFE的面积为6,求△ABD的面积.
21、如图ΔABC中,∠C=90°,
BC
=
8cm,
AC
=
6cm,点P从B出发,沿BC方向以2cm/s的速度移动,点Q从C出发,沿CA方向以1cm/s的速度移动.若P、Q分别同时从B、C出发,经过多少时间ΔCPQ与ΔCBA相似?
22、如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,。
⑴求证:△ABF∽△CEB;
⑵若△DEF的面积为2,求□ABCD的面积。
23、如图,四边形DEFG是ΔABC的内接矩形,如果ΔABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,求y关于x的函数关系式.
24、如图,梯形ABCD中.AB∥CD.且AB=2CD,E,F分别是AB,BC的中点。EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
25、如图,
等边⊿ABC,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明⊿ABD≌⊿BCE.
(2)⊿AEF与⊿ABE相似吗?说说你的理由.
(3)BD2=AD·DF吗?请说明理由.
26、如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.
27、如图所示在△OAB中,O为坐标原点,横、纵轴的单位长度相同,A、B的坐标分别为(8,6),(16,0),点P沿OA边从点O开始向终点A运动,速度每秒1个单位,点Q沿BO边从B点开始向终点O运动,速度每秒2个单位,如果P、Q同时出发,用t(秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动。
求(1)几秒时PQ∥AB
(2)设△OPQ的面积为y,求y与t的函数关系式.
(3)△OPQ与△OAB能否相似,若能,求出点P的坐标,若不能,试说明理由
南强中学2020年九年级上册《图形的相似》单元测试题答案
一、选择题:1.D;
2.
B;
3.A;
4.B;
5.A;6.
C;7.C;8.C
二、填空题:9.
10.
11.
;
12.
2.4;
13.
;
14.
4:3
15.
60
40;
16.
三、解答题:
17.有题意可得
解得
18.
有题意可得即
解得
19.(1)B(2.1)
(2)略
20.(1),
①时,解得=S
②时,解得=S
(1)略
(1),
(2)
25.
(1)SAS证明
(2)通过证明
证明
(3)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
