北师大版九年级数学下册 2.4 二次函数的应用 同步测试题(Word版 有答案)
文档属性
| 名称 | 北师大版九年级数学下册 2.4 二次函数的应用 同步测试题(Word版 有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 134.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览


文档简介
2.4
二次函数的应用
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
?1.
一个正方形和一个长方形的周长和为厘米,其中正方形的边长为厘米,长方形的一边为厘米,则这两个图形面积的和与之间的函数表达式为(
)
A.
B.
C.
D.
?
2.
一个运动员打高尔夫球,若球的飞行高度与水平距离之间的函数表达式为,则高尔夫球在飞行过程中的最大高度为(
)
A.
B.
C.
D.
?
3.
有人结伴去旅游共需支出??元,若??与??之间满足解析式,要使总支出最少,此时人数为(?
?
?
?
)
A.
B.
C.
D.
?
4.
用长的绳子围成一个矩形,如果这个矩形的一边长为?,面积是?,则与的函数关系式为(
)
A.
B.
C.
D.
?
5
如图所示的抛物线=的对称轴为直线=,则下列结论中错误的是(
)
A.
B.
C.=
D.=
?6.
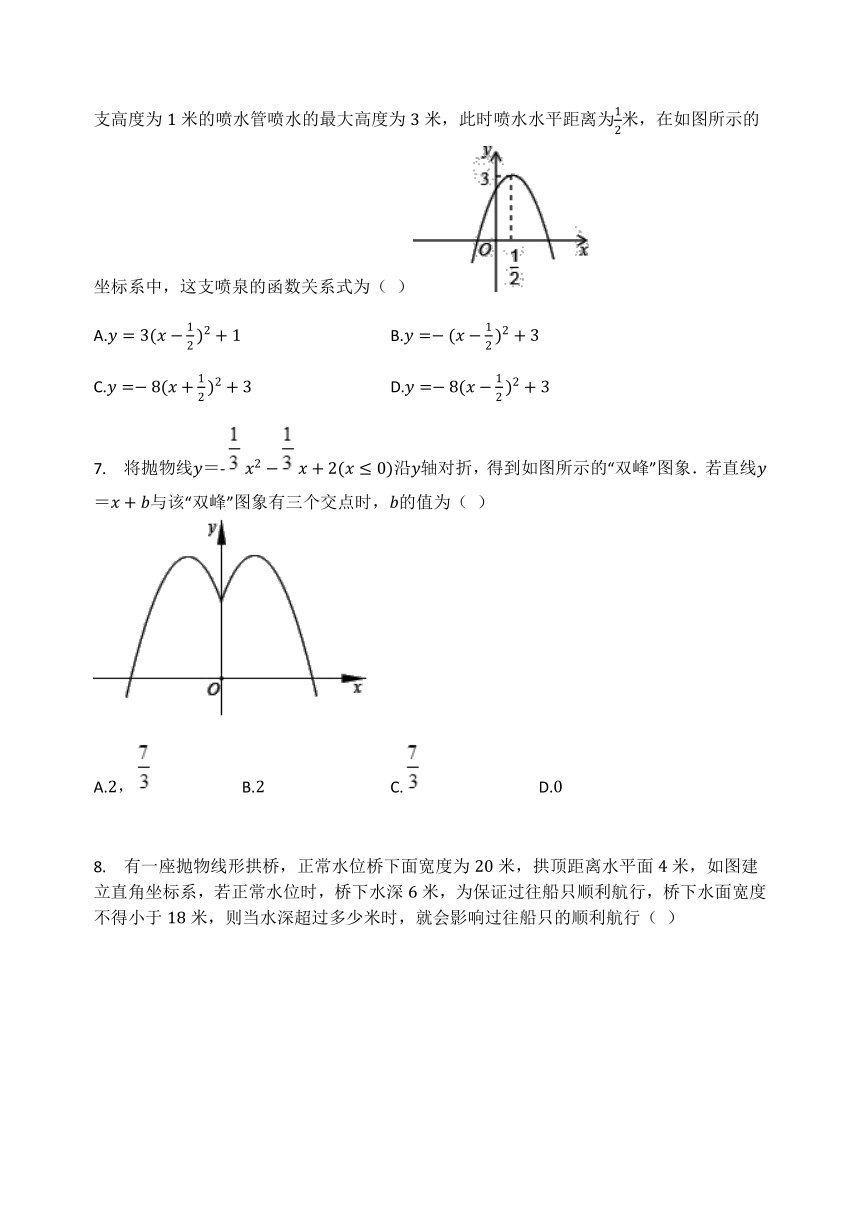
龙游已连续年列中国最具投资潜力中小城市百强,位次由年的位上升到年的第位,而龙游的荣昌广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为米的喷水管喷水的最大高度为米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数关系式为(
)
A.
B.
C.
D.
7.
将抛物线=-沿轴对折,得到如图所示的“双峰”图象.若直线=与该“双峰”图象有三个交点时,的值为(
)
A.,
B.
C.
D.
?
8.
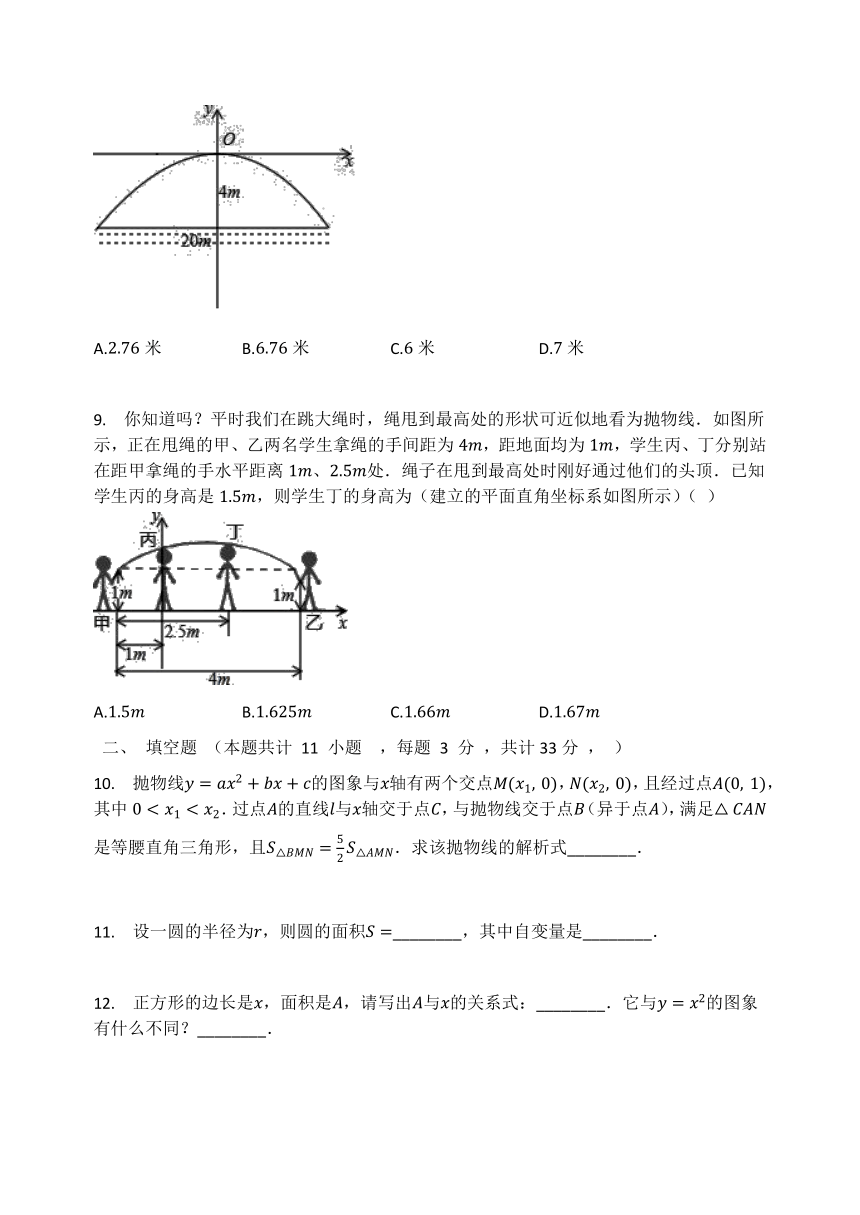
有一座抛物线形拱桥,正常水位桥下面宽度为米,拱顶距离水平面米,如图建立直角坐标系,若正常水位时,桥下水深米,为保证过往船只顺利航行,桥下水面宽度不得小于米,则当水深超过多少米时,就会影响过往船只的顺利航行(
)
A.米
B.米
C.米
D.米
?
9.
你知道吗?平时我们在跳大绳时,绳甩到最高处的形状可近似地看为抛物线.如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为,距地面均为,学生丙、丁分别站在距甲拿绳的手水平距离、处.绳子在甩到最高处时刚好通过他们的头顶.已知学生丙的身高是,则学生丁的身高为(建立的平面直角坐标系如图所示)(
)
A.
B.
C.
D.
二、
填空题
(本题共计
11
小题
,每题
3
分
,共计33分
,
)
?
10.
抛物线的图象与轴有两个交点,,且经过点,其中.过点的直线与轴交于点,与抛物线交于点(异于点),满足是等腰直角三角形,且.求该抛物线的解析式________.
?
11.
设一圆的半径为,则圆的面积________,其中自变量是________.
?
12.
正方形的边长是,面积是,请写出与的关系式:________.它与的图象有什么不同?________.
?
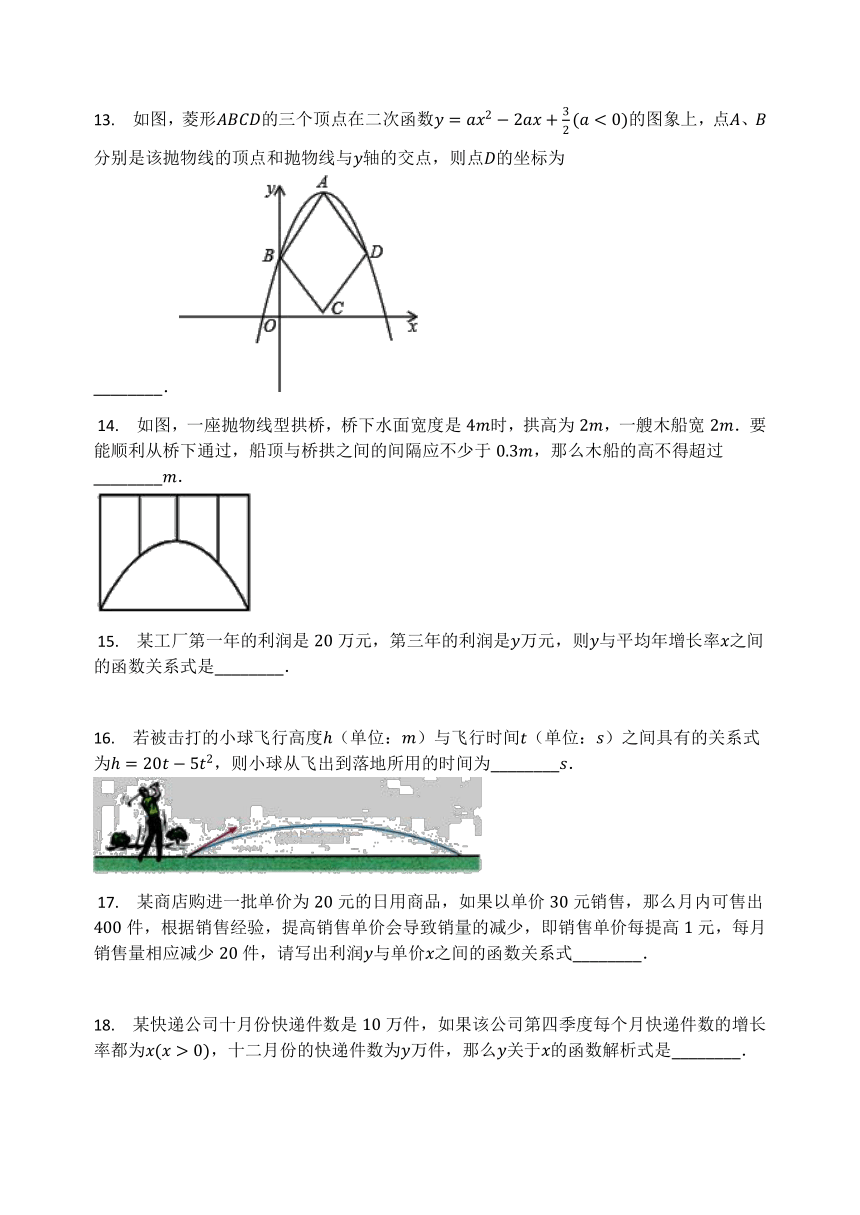
13.
如图,菱形的三个顶点在二次函数的图象上,点、分别是该抛物线的顶点和抛物线与轴的交点,则点的坐标为________.
?14.
如图,一座抛物线型拱桥,桥下水面宽度是时,拱高为,一艘木船宽.要能顺利从桥下通过,船顶与桥拱之间的间隔应不少于,那么木船的高不得超过________.
?15.
某工厂第一年的利润是万元,第三年的利润是万元,则与平均年增长率之间的函数关系式是________.
?
16.
若被击打的小球飞行高度(单位:)与飞行时间(单位:)之间具有的关系式为,则小球从飞出到落地所用的时间为________.
?17.
某商店购进一批单价为元的日用商品,如果以单价元销售,那么月内可售出件,根据销售经验,提高销售单价会导致销量的减少,即销售单价每提高元,每月销售量相应减少件,请写出利润与单价之间的函数关系式________.
?
18.
某快递公司十月份快递件数是万件,如果该公司第四季度每个月快递件数的增长率都为,十二月份的快递件数为万件,那么关于的函数解析式是________.
?
19.
某商品的进价为每件元,售价为每件元,每个月可卖出件;如果每件商品的售价上涨元,则每个月少卖件(每件售价不能高于元).设每件商品的售价上涨元(为正整数)月销售利润为元,当________元时,最大利润________元.
?
20.
如图,在平面直角坐标系中,二次函数的图象过正方形的三个顶点、、,则的值是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
某商场销售一种成本为每件元的商品,销售过程中发现,每月销售量(件)与销售单价(元)之间的关系可近似的看作一次函数:.
(1)设商场销售该种商品每月获得利润为(元),写出与之间的函数关系式;
(2)如果商场想要销售该种商品每月获得元的利润,那么每月成本至少多少元?
(3)为了保护环境,政府部门要求用更加环保的新产品替代该种商品,商场若销售新产品,每月销售量与销售价格之间的关系与原产品的销售情况相同,新产品为每件元,同时对商场的销售量每月不小于件的商场,政府部门给予每件元的补贴,试求定价多少时,新产品每月可获得销售利润最大?并求最大利润.
?
22.
某商店购进一种商品,每件商品进价元.试销中发现这种商品每天的销售量(件)与每件销售价(元)的关系数据如下:
(1)已知与满足一次函数关系,根据上表,求出与之间的关系式(不写出自变量的取值范围);
(2)如果商店销售这种商品,每天要获得元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为(元),求出与之间的关系式,并求出每件商品销售价定为多少元时利润最大?
?23.
某商场将进货单价为元的裤子,按元/件出售时,每月能卖出件,已知该商场裤子每涨价元月销量减少件.若这种裤子售价为元/件,该裤子获得的利润为元,请写出与的函数关系式.
?
24.
如图,在平面直角坐标系中,二次函数的图象与轴交于点,与轴交于,两点,其中点的坐标为,点为该二次函数在第二象限内图象上的动点,点的坐标为,连接.
求该二次函数的表达式及点的坐标;
连接,过点作轴于点,当以,,为顶点的三角形与相似时,求的值;
连接,以,为邻边作平行四边形,直线交轴于点.
①当点落在该二次函数图象上时,求点的坐标;
②在点从点到点运动过程中(点与点不重合),直接写出点在轴上的运动的路径长.
?
25.
七年级()班的全体同学排成一列步行去市博物馆参加科技活动,小涛担任通信员.在队伍中,小涛先数了一下他前后的人数,发现前面的人数是后面人数的倍,他往前超了名同学后,发现前面的人数和后面的人数一样.
七年级()班有多少名同学?
这些同学要通过一座长米的大桥,安全起见,相邻两个同学间保持相同的固定距离,队伍前进的速度为米秒,从第一名同学刚上桥到全体通过大桥用了秒,则队伍的全长为多少米?
在()的条件下,排在队尾的小刚想把一则通知送到队伍最前面的小婷手中,若小刚从队尾追赶小婷的速度是米秒,他能在秒内追上小婷吗?说明你的理由.
?
26.
某网店专售一品牌牙膏,其成本为元/支,销售中发现,该商品每天的销售量(支)与销售单价(元/支)之间存在如图所示的关系.
(1)请求出与之间的函数关系式;
(2)该品牌牙膏销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)在武汉爆发“新型冠状病毒”疫情期间,该网店店主决定从每天获得的利润中抽出元捐赠给武汉,为了保证捐款后每天剩余的利润不低于元,在抗“新型冠状病毒”疫情期间,市场监督管理局加大了对线上、线下商品销售的执法力度,对商品售价超过成本价的的商家进行处罚,请你给该网店店主提供一个合理化的销售单价范围.
参考答案
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
)
1.
【答案】
D
【解答】
解:∵
一个正方形和一个长方形的周长和为厘米,其中正方形的边长为厘米,长方形的一边为厘米,
∴
长方形的令一边为:厘米,
则这两个图形面积的和与之间的函数表达式为:.
故选:.
2.
【答案】
A
【解答】
解:在中,
当时,有最大值为.
则高尔夫球在飞行过程中的最大高度为.
故选.
3.
【答案】
C
【解答】
解:,
当时,.
故选.
4.
【答案】
C
【解答】
解:由题意得:.
故选.
5.
【答案】
C
【解答】
由图象开口向下,可知,
与轴的交点在轴的下方,可知,
又对称轴方程为,所以,所以,
∴
,故①正确;
由图象可知当时,,
∴
,故②错误;
由图象可知,
∵
,
∴
,即,
∴
,故③正确;
假设方程的一个根为,把代入方程可得,
整理可得,
两边同时乘可得,
即方程有一个根为,
由②可知,而当是方程的根,
∴
是方程的根,即假设成立,故④正确;
综上可知正确的结论有三个,
6.
【答案】
D
【解答】
解:∵
一支高度为米的喷水管喷水的最大高度为米,此时喷水水平距离为米,
∴
顶点坐标为,
设抛物线的解析式为,
而抛物线还经过,
∴
,
∴
,
∴
抛物线的解析式为.
故选.
7.
【答案】
【解答】
将抛物结沿轴对折,得到抛物线为
由抛物线可知抛物线与轴的交点为
把点代入求得
由整理得
当,即时,直线与该“双峰”图象有三个交点,
由图象可知若直线与该“双峰”图象有三个交点时,的值是和
故选:.
8.
【答案】
B
【解答】
解:设该抛物线的解析式为,在正常水位下,代入解析式可得
故此抛物线的解析式为.
因为桥下水面宽度不得小于米
所以令时
可得米
此时水深米
即桥下水深米时正好通过,所以超过米时则不能通过.
故选.
9.
【答案】
B
【解答】
解:设抛物线的解析式为,
因为抛物线过点、、
所以有:
.
解之得.
所以.
当时,.
即丁的身高是米.
故选.
二、
填空题
(本题共计
11
小题
,每题
3
分
,共计33分
)
10.
【答案】
【解答】
解:如图,由抛物线经过,,,
其中,
可知抛物线开口向上,与轴两交点在正半轴,
∵
点,是等腰直角三角形,∴
,,
设直线解析式为,
将、两点坐标代入,得,解得,
直线解析式为,
∵
,两三角形同底,的高为,
∴
的高为,即点纵坐标为,把代入中,得,
即,
把、、三点坐标代入中,得
,
解得,
所以,抛物线解析式为,
故答案为:.
11.
【答案】
,
【解答】
解:由圆的面积公式得:
,自变量是.
12.
【答案】
,它与的图象完全一样
【解答】
解:∵
正方形的边长是,面积是,
∴
与的关系式为:,
∴
它与的图象完全一样.
故答案为:,它与的图象完全一样.
13.
【答案】
【解答】
解:∵
的对称轴是,与轴的交点坐标是
∴
点的坐标是
∵
菱形的三个顶点在二次函数的图象上,
点、分别是该抛物线的顶点和抛物线与轴的交点,
∴
点与点关于直线对称,
∴
点的坐标为.
故答案为:.
14.
【答案】
【解答】
解:以水面所在水平线为轴,过拱桥顶点作水平线的垂线,作为轴,建立坐标系,
设水平面与拱桥的交点,,顶点,
利用待定系数法设函数的解析式为代入点坐标,
求得:,
即抛物线的解析式为.
令,解得:,
船顶与桥拱之间的间隔应不少于,则木船的最高高度为.
故答案为:
15.
【答案】
【解答】
解:设增产率为,因为第一年的利润是万元,所以第二年的利润是,第三年的利润是,即,依题意得函数关系式:
???
故:??.
16.
【答案】
【解答】
解:依题意,令得:
,
得,
解得(舍去)或,
即小球从飞出到落地所用的时间为.
故答案为:.
17.
【答案】
【解答】
解:单价是元,则销量是:,
每件的盈利是元,
则利润,
根据且,解得:.
18.
【答案】
=
【解答】
根据题意得:=,
19.
【答案】
或,
【解答】
解:由题意得:
(且为整数);
.
∵
,
∴
当时,有最大值.
∵
,且为整数,
当时,,(元);
当时,,(元)
即当元或元时,每个月的利润最大,最大的月利润是元;
故答案为:或,.
20.
【答案】
【解答】
解:设正方形的对角线长为,
则,,;
把,的坐标代入解析式可得:
①,②,
①代入②得:,解得:,
则.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
想要每月获得元的利润,销售单价应定为元或元.
(3)当销售量每月不小于件时,即,
解得:,
由题意,得:
∴
当定价元时,新产品每月可获得销售利润最大值是元.
【解答】
解:(1)由题意,得:,
,
(2)由题意,得:,
解这个方程得:,,
答:想要每月获得元的利润,销售单价应定为元或元.
(3)当销售量每月不小于件时,即,
解得:,
由题意,得:
∴
当定价元时,新产品每月可获得销售利润最大值是元.
22.
【答案】
设该函数的表达式为=,根据题意,得
,
解得:.
故该函数的表达式为=;
根据题意得,
=,
解这个方程得,=,=,
故每件商品的销售价定为元或元时日利润为元;
根据题意,得
=
=
=,
∵
=?则抛物线开口向下,函数有最大值,
即当=时,的值最大,
∴
当销售单价为元时获得利润最大.
【解答】
设该函数的表达式为=,根据题意,得
,
解得:.
故该函数的表达式为=;
根据题意得,
=,
解这个方程得,=,=,
故每件商品的销售价定为元或元时日利润为元;
根据题意,得
=
=
=,
∵
=?则抛物线开口向下,函数有最大值,
即当=时,的值最大,
∴
当销售单价为元时获得利润最大.
23.
【答案】
解:根据题意可得:
.
【解答】
解:根据题意可得:
.
24.
【答案】
解:把代入得,
解得
∴
该二次函数的表达为.
当时,,
解得,
∴
点的坐标为;
设,
由,
分两种情况:
当时,,
∴
.
即,
解得,或(舍去).
当时,,
∴
,
即,
解得或(舍去)
综上所述,的值为或.
①∵
四边形为平行四边形,
∴
,.
∵
点向右平移个单位,再向上平移个单位得到点,
∴
点向右平移个单位,再向上平移个单位得到点.
∵
点,
∴
点.
∵
点落在二次函数的图象上
∴
,
解得,,
∴
点的坐标为;
②点在轴上的运动的路经长.
【解答】
解:把代入得,
解得
∴
该二次函数的表达为.
当时,,
解得,
∴
点的坐标为;
设,
由,
分两种情况:
当时,,
∴
.
即,
解得,或(舍去).
当时,,
∴
,
即,
解得或(舍去)
综上所述,的值为或.
①∵
四边形为平行四边形,
∴
,.
∵
点向右平移个单位,再向上平移个单位得到点,
∴
点向右平移个单位,再向上平移个单位得到点.
∵
点,
∴
点.
∵
点落在二次函数的图象上
∴
,
解得,,
∴
点的坐标为;
②点在轴上的运动的路经长.
25.
【答案】
()七年级()班有名同学
(2)队伍的全长为米
(3)不能,理由略
【解答】
此题暂无解答
26.
【答案】
(1);
(2)销售单价定为元时,每天最大利润为元;
(3)大于或等于元小于或等于元.
【解答】
(1)解:据题意设
将&代入得
解之得
…)与х之间的关系式为
(2)设每天的利润为元,则
…销售单价定为元时,每天最大利润为元.
(3),解得或
结合图像和二次函数的特点得出
又,即:
综合得
…按要求网店店主的销售单价范围为大于或等于元小于或等于元.
二次函数的应用
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
?1.
一个正方形和一个长方形的周长和为厘米,其中正方形的边长为厘米,长方形的一边为厘米,则这两个图形面积的和与之间的函数表达式为(
)
A.
B.
C.
D.
?
2.
一个运动员打高尔夫球,若球的飞行高度与水平距离之间的函数表达式为,则高尔夫球在飞行过程中的最大高度为(
)
A.
B.
C.
D.
?
3.
有人结伴去旅游共需支出??元,若??与??之间满足解析式,要使总支出最少,此时人数为(?
?
?
?
)
A.
B.
C.
D.
?
4.
用长的绳子围成一个矩形,如果这个矩形的一边长为?,面积是?,则与的函数关系式为(
)
A.
B.
C.
D.
?
5
如图所示的抛物线=的对称轴为直线=,则下列结论中错误的是(
)
A.
B.
C.=
D.=
?6.
龙游已连续年列中国最具投资潜力中小城市百强,位次由年的位上升到年的第位,而龙游的荣昌广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为米的喷水管喷水的最大高度为米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数关系式为(
)
A.
B.
C.
D.
7.
将抛物线=-沿轴对折,得到如图所示的“双峰”图象.若直线=与该“双峰”图象有三个交点时,的值为(
)
A.,
B.
C.
D.
?
8.
有一座抛物线形拱桥,正常水位桥下面宽度为米,拱顶距离水平面米,如图建立直角坐标系,若正常水位时,桥下水深米,为保证过往船只顺利航行,桥下水面宽度不得小于米,则当水深超过多少米时,就会影响过往船只的顺利航行(
)
A.米
B.米
C.米
D.米
?
9.
你知道吗?平时我们在跳大绳时,绳甩到最高处的形状可近似地看为抛物线.如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为,距地面均为,学生丙、丁分别站在距甲拿绳的手水平距离、处.绳子在甩到最高处时刚好通过他们的头顶.已知学生丙的身高是,则学生丁的身高为(建立的平面直角坐标系如图所示)(
)
A.
B.
C.
D.
二、
填空题
(本题共计
11
小题
,每题
3
分
,共计33分
,
)
?
10.
抛物线的图象与轴有两个交点,,且经过点,其中.过点的直线与轴交于点,与抛物线交于点(异于点),满足是等腰直角三角形,且.求该抛物线的解析式________.
?
11.
设一圆的半径为,则圆的面积________,其中自变量是________.
?
12.
正方形的边长是,面积是,请写出与的关系式:________.它与的图象有什么不同?________.
?
13.
如图,菱形的三个顶点在二次函数的图象上,点、分别是该抛物线的顶点和抛物线与轴的交点,则点的坐标为________.
?14.
如图,一座抛物线型拱桥,桥下水面宽度是时,拱高为,一艘木船宽.要能顺利从桥下通过,船顶与桥拱之间的间隔应不少于,那么木船的高不得超过________.
?15.
某工厂第一年的利润是万元,第三年的利润是万元,则与平均年增长率之间的函数关系式是________.
?
16.
若被击打的小球飞行高度(单位:)与飞行时间(单位:)之间具有的关系式为,则小球从飞出到落地所用的时间为________.
?17.
某商店购进一批单价为元的日用商品,如果以单价元销售,那么月内可售出件,根据销售经验,提高销售单价会导致销量的减少,即销售单价每提高元,每月销售量相应减少件,请写出利润与单价之间的函数关系式________.
?
18.
某快递公司十月份快递件数是万件,如果该公司第四季度每个月快递件数的增长率都为,十二月份的快递件数为万件,那么关于的函数解析式是________.
?
19.
某商品的进价为每件元,售价为每件元,每个月可卖出件;如果每件商品的售价上涨元,则每个月少卖件(每件售价不能高于元).设每件商品的售价上涨元(为正整数)月销售利润为元,当________元时,最大利润________元.
?
20.
如图,在平面直角坐标系中,二次函数的图象过正方形的三个顶点、、,则的值是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
某商场销售一种成本为每件元的商品,销售过程中发现,每月销售量(件)与销售单价(元)之间的关系可近似的看作一次函数:.
(1)设商场销售该种商品每月获得利润为(元),写出与之间的函数关系式;
(2)如果商场想要销售该种商品每月获得元的利润,那么每月成本至少多少元?
(3)为了保护环境,政府部门要求用更加环保的新产品替代该种商品,商场若销售新产品,每月销售量与销售价格之间的关系与原产品的销售情况相同,新产品为每件元,同时对商场的销售量每月不小于件的商场,政府部门给予每件元的补贴,试求定价多少时,新产品每月可获得销售利润最大?并求最大利润.
?
22.
某商店购进一种商品,每件商品进价元.试销中发现这种商品每天的销售量(件)与每件销售价(元)的关系数据如下:
(1)已知与满足一次函数关系,根据上表,求出与之间的关系式(不写出自变量的取值范围);
(2)如果商店销售这种商品,每天要获得元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为(元),求出与之间的关系式,并求出每件商品销售价定为多少元时利润最大?
?23.
某商场将进货单价为元的裤子,按元/件出售时,每月能卖出件,已知该商场裤子每涨价元月销量减少件.若这种裤子售价为元/件,该裤子获得的利润为元,请写出与的函数关系式.
?
24.
如图,在平面直角坐标系中,二次函数的图象与轴交于点,与轴交于,两点,其中点的坐标为,点为该二次函数在第二象限内图象上的动点,点的坐标为,连接.
求该二次函数的表达式及点的坐标;
连接,过点作轴于点,当以,,为顶点的三角形与相似时,求的值;
连接,以,为邻边作平行四边形,直线交轴于点.
①当点落在该二次函数图象上时,求点的坐标;
②在点从点到点运动过程中(点与点不重合),直接写出点在轴上的运动的路径长.
?
25.
七年级()班的全体同学排成一列步行去市博物馆参加科技活动,小涛担任通信员.在队伍中,小涛先数了一下他前后的人数,发现前面的人数是后面人数的倍,他往前超了名同学后,发现前面的人数和后面的人数一样.
七年级()班有多少名同学?
这些同学要通过一座长米的大桥,安全起见,相邻两个同学间保持相同的固定距离,队伍前进的速度为米秒,从第一名同学刚上桥到全体通过大桥用了秒,则队伍的全长为多少米?
在()的条件下,排在队尾的小刚想把一则通知送到队伍最前面的小婷手中,若小刚从队尾追赶小婷的速度是米秒,他能在秒内追上小婷吗?说明你的理由.
?
26.
某网店专售一品牌牙膏,其成本为元/支,销售中发现,该商品每天的销售量(支)与销售单价(元/支)之间存在如图所示的关系.
(1)请求出与之间的函数关系式;
(2)该品牌牙膏销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)在武汉爆发“新型冠状病毒”疫情期间,该网店店主决定从每天获得的利润中抽出元捐赠给武汉,为了保证捐款后每天剩余的利润不低于元,在抗“新型冠状病毒”疫情期间,市场监督管理局加大了对线上、线下商品销售的执法力度,对商品售价超过成本价的的商家进行处罚,请你给该网店店主提供一个合理化的销售单价范围.
参考答案
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
)
1.
【答案】
D
【解答】
解:∵
一个正方形和一个长方形的周长和为厘米,其中正方形的边长为厘米,长方形的一边为厘米,
∴
长方形的令一边为:厘米,
则这两个图形面积的和与之间的函数表达式为:.
故选:.
2.
【答案】
A
【解答】
解:在中,
当时,有最大值为.
则高尔夫球在飞行过程中的最大高度为.
故选.
3.
【答案】
C
【解答】
解:,
当时,.
故选.
4.
【答案】
C
【解答】
解:由题意得:.
故选.
5.
【答案】
C
【解答】
由图象开口向下,可知,
与轴的交点在轴的下方,可知,
又对称轴方程为,所以,所以,
∴
,故①正确;
由图象可知当时,,
∴
,故②错误;
由图象可知,
∵
,
∴
,即,
∴
,故③正确;
假设方程的一个根为,把代入方程可得,
整理可得,
两边同时乘可得,
即方程有一个根为,
由②可知,而当是方程的根,
∴
是方程的根,即假设成立,故④正确;
综上可知正确的结论有三个,
6.
【答案】
D
【解答】
解:∵
一支高度为米的喷水管喷水的最大高度为米,此时喷水水平距离为米,
∴
顶点坐标为,
设抛物线的解析式为,
而抛物线还经过,
∴
,
∴
,
∴
抛物线的解析式为.
故选.
7.
【答案】
【解答】
将抛物结沿轴对折,得到抛物线为
由抛物线可知抛物线与轴的交点为
把点代入求得
由整理得
当,即时,直线与该“双峰”图象有三个交点,
由图象可知若直线与该“双峰”图象有三个交点时,的值是和
故选:.
8.
【答案】
B
【解答】
解:设该抛物线的解析式为,在正常水位下,代入解析式可得
故此抛物线的解析式为.
因为桥下水面宽度不得小于米
所以令时
可得米
此时水深米
即桥下水深米时正好通过,所以超过米时则不能通过.
故选.
9.
【答案】
B
【解答】
解:设抛物线的解析式为,
因为抛物线过点、、
所以有:
.
解之得.
所以.
当时,.
即丁的身高是米.
故选.
二、
填空题
(本题共计
11
小题
,每题
3
分
,共计33分
)
10.
【答案】
【解答】
解:如图,由抛物线经过,,,
其中,
可知抛物线开口向上,与轴两交点在正半轴,
∵
点,是等腰直角三角形,∴
,,
设直线解析式为,
将、两点坐标代入,得,解得,
直线解析式为,
∵
,两三角形同底,的高为,
∴
的高为,即点纵坐标为,把代入中,得,
即,
把、、三点坐标代入中,得
,
解得,
所以,抛物线解析式为,
故答案为:.
11.
【答案】
,
【解答】
解:由圆的面积公式得:
,自变量是.
12.
【答案】
,它与的图象完全一样
【解答】
解:∵
正方形的边长是,面积是,
∴
与的关系式为:,
∴
它与的图象完全一样.
故答案为:,它与的图象完全一样.
13.
【答案】
【解答】
解:∵
的对称轴是,与轴的交点坐标是
∴
点的坐标是
∵
菱形的三个顶点在二次函数的图象上,
点、分别是该抛物线的顶点和抛物线与轴的交点,
∴
点与点关于直线对称,
∴
点的坐标为.
故答案为:.
14.
【答案】
【解答】
解:以水面所在水平线为轴,过拱桥顶点作水平线的垂线,作为轴,建立坐标系,
设水平面与拱桥的交点,,顶点,
利用待定系数法设函数的解析式为代入点坐标,
求得:,
即抛物线的解析式为.
令,解得:,
船顶与桥拱之间的间隔应不少于,则木船的最高高度为.
故答案为:
15.
【答案】
【解答】
解:设增产率为,因为第一年的利润是万元,所以第二年的利润是,第三年的利润是,即,依题意得函数关系式:
???
故:??.
16.
【答案】
【解答】
解:依题意,令得:
,
得,
解得(舍去)或,
即小球从飞出到落地所用的时间为.
故答案为:.
17.
【答案】
【解答】
解:单价是元,则销量是:,
每件的盈利是元,
则利润,
根据且,解得:.
18.
【答案】
=
【解答】
根据题意得:=,
19.
【答案】
或,
【解答】
解:由题意得:
(且为整数);
.
∵
,
∴
当时,有最大值.
∵
,且为整数,
当时,,(元);
当时,,(元)
即当元或元时,每个月的利润最大,最大的月利润是元;
故答案为:或,.
20.
【答案】
【解答】
解:设正方形的对角线长为,
则,,;
把,的坐标代入解析式可得:
①,②,
①代入②得:,解得:,
则.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
想要每月获得元的利润,销售单价应定为元或元.
(3)当销售量每月不小于件时,即,
解得:,
由题意,得:
∴
当定价元时,新产品每月可获得销售利润最大值是元.
【解答】
解:(1)由题意,得:,
,
(2)由题意,得:,
解这个方程得:,,
答:想要每月获得元的利润,销售单价应定为元或元.
(3)当销售量每月不小于件时,即,
解得:,
由题意,得:
∴
当定价元时,新产品每月可获得销售利润最大值是元.
22.
【答案】
设该函数的表达式为=,根据题意,得
,
解得:.
故该函数的表达式为=;
根据题意得,
=,
解这个方程得,=,=,
故每件商品的销售价定为元或元时日利润为元;
根据题意,得
=
=
=,
∵
=?则抛物线开口向下,函数有最大值,
即当=时,的值最大,
∴
当销售单价为元时获得利润最大.
【解答】
设该函数的表达式为=,根据题意,得
,
解得:.
故该函数的表达式为=;
根据题意得,
=,
解这个方程得,=,=,
故每件商品的销售价定为元或元时日利润为元;
根据题意,得
=
=
=,
∵
=?则抛物线开口向下,函数有最大值,
即当=时,的值最大,
∴
当销售单价为元时获得利润最大.
23.
【答案】
解:根据题意可得:
.
【解答】
解:根据题意可得:
.
24.
【答案】
解:把代入得,
解得
∴
该二次函数的表达为.
当时,,
解得,
∴
点的坐标为;
设,
由,
分两种情况:
当时,,
∴
.
即,
解得,或(舍去).
当时,,
∴
,
即,
解得或(舍去)
综上所述,的值为或.
①∵
四边形为平行四边形,
∴
,.
∵
点向右平移个单位,再向上平移个单位得到点,
∴
点向右平移个单位,再向上平移个单位得到点.
∵
点,
∴
点.
∵
点落在二次函数的图象上
∴
,
解得,,
∴
点的坐标为;
②点在轴上的运动的路经长.
【解答】
解:把代入得,
解得
∴
该二次函数的表达为.
当时,,
解得,
∴
点的坐标为;
设,
由,
分两种情况:
当时,,
∴
.
即,
解得,或(舍去).
当时,,
∴
,
即,
解得或(舍去)
综上所述,的值为或.
①∵
四边形为平行四边形,
∴
,.
∵
点向右平移个单位,再向上平移个单位得到点,
∴
点向右平移个单位,再向上平移个单位得到点.
∵
点,
∴
点.
∵
点落在二次函数的图象上
∴
,
解得,,
∴
点的坐标为;
②点在轴上的运动的路经长.
25.
【答案】
()七年级()班有名同学
(2)队伍的全长为米
(3)不能,理由略
【解答】
此题暂无解答
26.
【答案】
(1);
(2)销售单价定为元时,每天最大利润为元;
(3)大于或等于元小于或等于元.
【解答】
(1)解:据题意设
将&代入得
解之得
…)与х之间的关系式为
(2)设每天的利润为元,则
…销售单价定为元时,每天最大利润为元.
(3),解得或
结合图像和二次函数的特点得出
又,即:
综合得
…按要求网店店主的销售单价范围为大于或等于元小于或等于元.
