2020年鲁教版(五四制)七年级数学上册综合测试(Word版 含解析)
文档属性
| 名称 | 2020年鲁教版(五四制)七年级数学上册综合测试(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 10:53:44 | ||
图片预览



文档简介
七年级数学综合测试
一.选择题(共12小题,满分36分,每小题3分)
1.已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
2.下列说法正确的是( )
A.4的算术平方根是2
B.﹣8的立方根不存在
C.1的平方根是1
D.﹣4的平方根是±2
3.在3,0,﹣2,﹣四个数中,最小的数是( )
A.3
B.0
C.﹣2
D.﹣
4.如图,已知棋子“车”的坐标为(﹣2,﹣1),棋子“马”的坐标为(1,﹣1),则棋子“炮”的坐标为( )
A.(3,2)
B.(﹣3,2)
C.(3,﹣2)
D.(﹣3,﹣2)
5.下列函数中,是一次函数的是( )
A.y=+1
B.y=+1
C.y=x2+2
D.y=﹣x
6.如图,在△ABC中,AB=AC,AD是边BC上的中线,若AB=5,BC=6,则AD的长为( )
A.3
B.
C.4
D.
7.设的小数部分为b,那么(4+b)b的值是( )
A.1
B.是一个有理数
C.3
D.无法确定
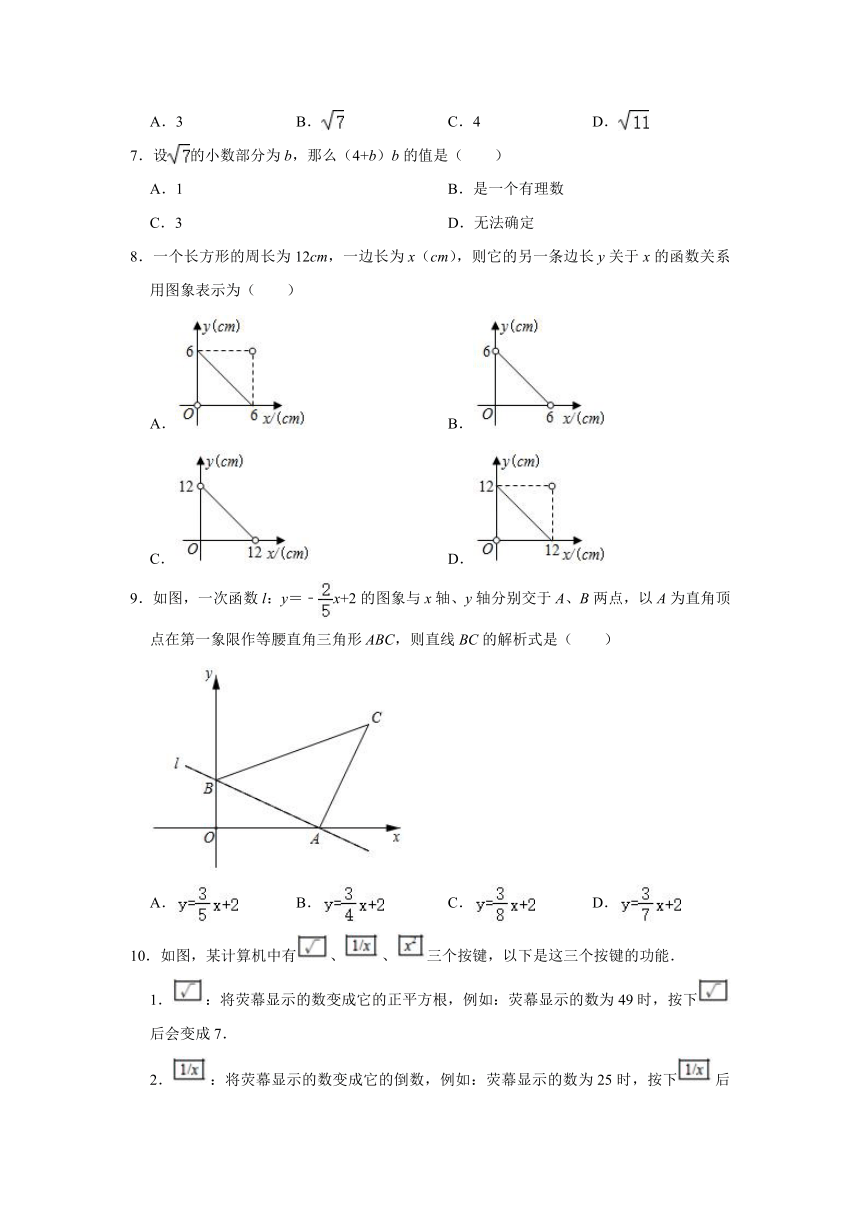
8.一个长方形的周长为12cm,一边长为x(cm),则它的另一条边长y关于x的函数关系用图象表示为( )
A.
B.
C.
D.
9.如图,一次函数l:y=﹣x+2的图象与x轴、y轴分别交于A、B两点,以A为直角顶点在第一象限作等腰直角三角形ABC,则直线BC的解析式是( )
A.
B.
C.
D.
10.如图,某计算机中有、、三个按键,以下是这三个按键的功能.
1.:将荧幕显示的数变成它的正平方根,例如:荧幕显示的数为49时,按下后会变成7.
2.:将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下后会变成0.04.
3.:将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下后会变成36.
若荧幕显示的数为100时,小刘第一下按,第二下按,第三下按,之后以、、的顺序轮流按,则当他按了第100下后荧幕显示的数是多少( )
A.0.01
B.0.1
C.10
D.100
11.已知点A(1,3),B(﹣2,3),则A,B两点间的距离是( )
A.4个单位长度
B.3个单位长度
C.2个单位长度
D.1个单位长度
12.如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:(1)∠DEF=∠DFE;(2)AE=AF;(3)AD平分∠EDF;(4)EF垂直平分AD.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共6小题,满分18分,每小题3分)
13.已知点P1(x1,y1),P2(x2,y2)是一次函数y=﹣5x+b图象上的两个点,若x1<x2,则y1
y2(填“>”“<”或“=”).
14.一蜡烛高20厘米,点燃后平均每小时燃掉4厘米,则蜡烛点燃后剩余的高度h(厘米)与燃烧时间t(时)之间的关系式是h=
(0≤t≤5).
15.已知点A(4,3),AB∥y轴,且AB=3,则B点的坐标为
.
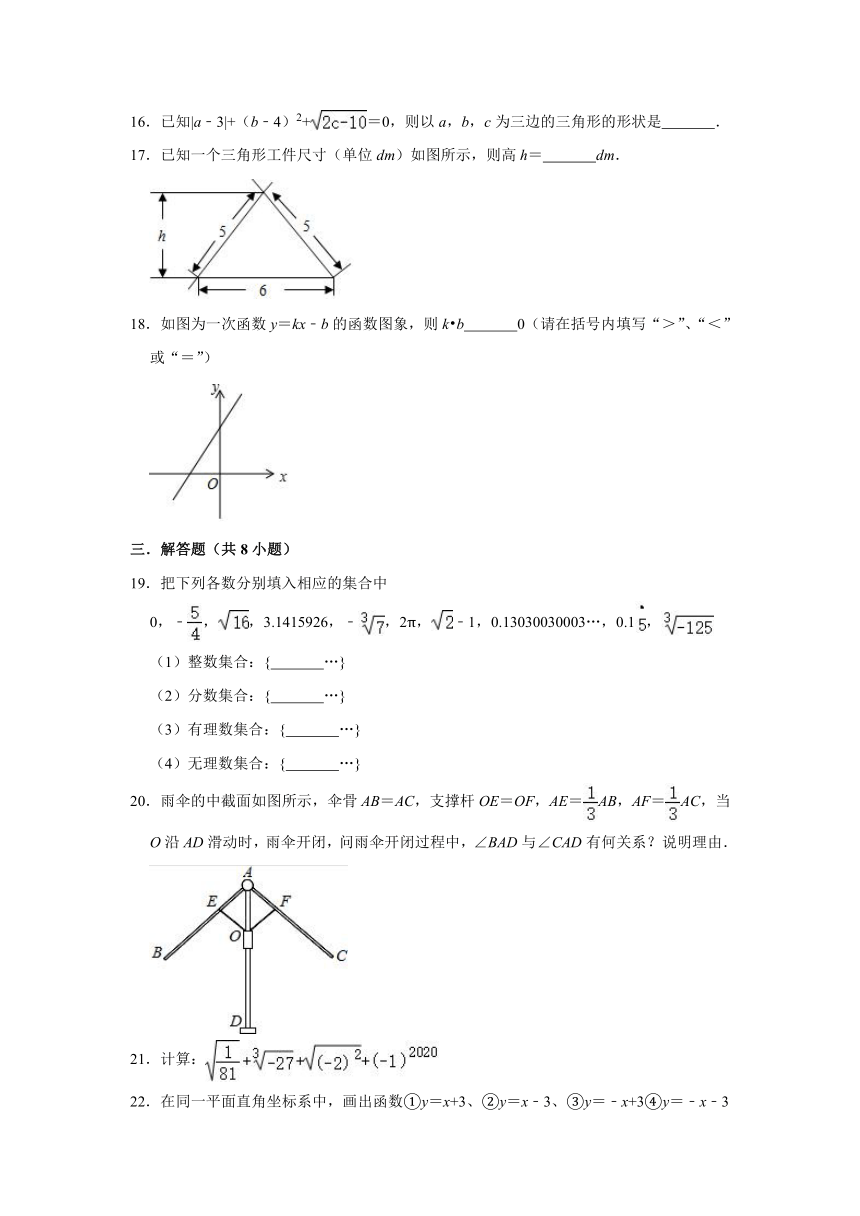
16.已知|a﹣3|+(b﹣4)2+=0,则以a,b,c为三边的三角形的形状是
.
17.已知一个三角形工件尺寸(单位dm)如图所示,则高h=
dm.
18.如图为一次函数y=kx﹣b的函数图象,则k?b
0(请在括号内填写“>”、“<”或“=”)
三.解答题(共8小题)
19.把下列各数分别填入相应的集合中
0,﹣,,3.1415926,﹣,2π,﹣1,0.13030030003…,0.1,
(1)整数集合:{
…}
(2)分数集合:{
…}
(3)有理数集合:{
…}
(4)无理数集合:{
…}
20.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
21.计算:
22.在同一平面直角坐标系中,画出函数①y=x+3、②y=x﹣3、③y=﹣x+3④y=﹣x﹣3的图象,并找出每两个函数图象之间的共同特征.
23.作图:如图,请按要求在8×8的正方形网格中作图
(1)请在图1中画一个钝角△ABC,使它有一边与该边上的高线长度相等;
(2)请在图2画一个五边形ABCDE,是轴对称图形,且∠ABC=90°.
24.如图,小明爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算这块土地的面积,以便估算产量.小明测得AB=8m,AD=6m,CD=24m,BC=26m,又已知∠A=90°.求这块土地的面积.
25.甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟
米,乙在A地时距地面的高度b为
米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
26.某水果市场销售一种香蕉.甲店的香蕉价格为4元/kg;乙店的香蕉价格为5元/kg,若一次购买6kg以上,超过6kg部分的价格打7折.
(1)设购买香蕉xkg,付款金额y元,分别就两店的付款金额写出y关于x的函数解析式;
(2)到哪家店购买香蕉更省钱?请说明理由.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为P1、P2,
∴OP=OP1=OP2且∠P1OP2=2∠AOB=60°,
∴故△P1OP2是等边三角形.
故选:C.
2.解:A、4的算术平方根为2,正确;
B、﹣8的立方根为﹣2,错误;
C、1的平方根为1和﹣1,错误;
D、﹣4没有平方根,错误,
故选:A.
3.解:∵﹣2<﹣<0<3,
∴四个数中,最小的数是﹣2,
故选:C.
4.解:如图,
棋子“炮”的坐标为(3,﹣2).
故选:C.
5.解:A、不是一次函数,故此选项不合题意;
B、不是一次函数,故此选项不合题意;
C、不是一次函数,是二次函数,故此选项不合题意;
D、是一次函数,故此选项符合题意;
故选:D.
6.解:∵在△ABC中,AB=AC,AD是边BC上的中线,
∴BD=BC=3,AD⊥BC,
∵在Rt△ADB中,AB=5,
∴AD===4.
故选:C.
7.解:∵的小数部分为b,
∴b=﹣2,
把b=﹣2代入式子(4+b)b中,
原式=(4+b)b=(4+﹣2)×(﹣2)=3.
故选:C.
8.解:∵长方形的周长为12cm,一边长为x(cm),
则它的另一条边长y关于x的函数关系为:
y=6﹣x(0<x<6).
当x=0时,y=6,
当y=0时,x=6.
所以直线y=6﹣x与x轴、y轴的交点分别为(6,0)、(0,6).
所以B选项符合题意.
故选:B.
9.解:∵一次函数y=﹣x+2中,
令x=0得:y=2;令y=0,解得x=5,
∴B的坐标是(0,2),A的坐标是(5,0).
若∠BAC=90°,如图,作CE⊥x轴于点E,
∵∠BAC=90°,
∴∠OAB+∠CAE=90°,
又∵∠CAE+∠ACE=90°,
∴∠ACE=∠BAO.
在△ABO与△CAE中
,
∴△ABO≌△CAE(AAS),
∴OB=AE=2,OA=CE=5,
∴OE=OA+AE=2+5=7.
则C的坐标是(7,5).
设直线BC的解析式是y=kx+b,
根据题意得:,
解得,
∴直线BC的解析式是y=x+2.
故选:D.
10.解:根据题意得:=10,
=0.1,
0.12=0.01,
=0.1,
=10,
102=100,
100÷6=16…4,
则第100次为0.1.
故选:B.
11.解:由点A(1,3),B(﹣2,3)知,AB=|1﹣(﹣2)|=3,即A,B两点间的距离是3个单位长度.
故选:B.
12.解:∵AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC
∴△ABC是等腰三角形,AD⊥BC,BD=CD,∠BED=∠DFC=90°
∴DE=DF
∴AD垂直平分EF
∴(4)错误;
又∵AD所在直线是△ABC的对称轴,
∴(1)∠DEF=∠DFE;(2)AE=AF;(3)AD平分∠EDF.
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
13.解:∵k=﹣5<0,
∴y值随x值增大而减小.
又∵点P1(x1,y1),P2(x2,y2)是一次函数y=﹣5x+b图象上的两个点,且x1<x2,
∴y1>y2.
故答案为:>.
14.解:∵蜡烛点燃后平均每小时燃掉4厘米,
∴t小时燃掉4t厘米,
由题意知:h=20﹣4t.
15.解:∵A(4,3),AB∥y轴,
∴点B的横坐标为4,
∵AB=3,
∴点B的纵坐标为3+3=6或3﹣3=0,
∴B点的坐标为(4,0)或(4,6).故填(4,0)或(4,6).
16.解:∵|a﹣3|+(b﹣4)2+=0,
∴a﹣3=0,b﹣4=0,2c﹣10=0,
解得:a=3,b=4,c=5,
∴a2+b2=c2,
∴以a,b,c为三边的三角形是直角三角形,
故答案为:直角三角形.
17.解:
过点A作AD⊥BC于点D,则AD=h,
∵AB=AC=5dm,BC=6dm,
∴AD是BC的垂直平分线,
∴BD=BC=3dm.
在Rt△ABD中,
AD=dm,即h=4(dm).
答:h的长为4dm.
故答案为:4.
18.解:∵一次函数经过一、三象限,
∴k>0,
∵一次函数与y轴的交于正半轴,
∴﹣b>0,
∴b<0,
∴k?b,<0,
故答案为:<
三.解答题(共8小题)
19.解:=4,=﹣5,
(1)整数集合:{0,,,…};
(2)分数集合:{﹣,3.1415926,0.1,…};
(3)有理数集合:{0,﹣,,3.1415926,0.1,,…};
(4)无理数集合:{﹣,2π,﹣1,0.13030030003…,…}.
故答案为:0,,;﹣,3.1415926,0.1;0,﹣,,3.1415926,0.1,;﹣,2π,﹣1,0.13030030003….
20.解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,
理由如下:
∵AB=AC,AE=AB,AF=AC,
∴AE=AF,
在△AOE与△AOF中,
,
∴△AOE≌△AOF(SSS),
∴∠BAD=∠CAD.
21.解:
=﹣3+2+1
=
22.解:列表:
如图所示:
由图可得,①和②图象互相平行,①和③图象与y轴交点相同,①和④图象与x轴交点相同,②和③图象与x轴交点相同,②和④图象与y轴交点相同,③和④图象互相平行.
23.解:(1)
(2)
24.解:连接BD,
∵∠A=90°,
∴BD2=AD2+AB2=100
则BD2+CD2=100+576=676=262=BC2,因此∠CBD=90°,
S四边形ABCD=S△ADB+S△CBD=AD?AB+BD?CD=×6×8+×24×10=144(平方米).
25.解:(1)甲登山上升的速度是:(300﹣100)÷20=10(米/分钟),
b=15÷1×2=30.
故答案为:10;30;
(2)当0≤x<2时,y=15x;
当x≥2时,y=30+10×3(x﹣2)=30x﹣30.
当y=30x﹣30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=;
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100﹣(30x﹣30)=70时,解得:x=3;
当30x﹣30﹣(10x+100)=70时,解得:x=10;
当300﹣(10x+100)=70时,解得:x=13.
答:登山3分钟、10分钟或13分钟时,甲、乙两人距地面的高度差为70米.
26.解:(1)甲商店:y=4x
乙商店:y=.
(2)当x<6时,
此时甲商店比较省钱,
当x≥6时,
令4x=30+3.5(x﹣6),
解得:x=18,
此时甲乙商店的费用一样,
当x<18时,
此时甲商店比较省钱,
当x>18时,
此时乙商店比较省钱.
一.选择题(共12小题,满分36分,每小题3分)
1.已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
2.下列说法正确的是( )
A.4的算术平方根是2
B.﹣8的立方根不存在
C.1的平方根是1
D.﹣4的平方根是±2
3.在3,0,﹣2,﹣四个数中,最小的数是( )
A.3
B.0
C.﹣2
D.﹣
4.如图,已知棋子“车”的坐标为(﹣2,﹣1),棋子“马”的坐标为(1,﹣1),则棋子“炮”的坐标为( )
A.(3,2)
B.(﹣3,2)
C.(3,﹣2)
D.(﹣3,﹣2)
5.下列函数中,是一次函数的是( )
A.y=+1
B.y=+1
C.y=x2+2
D.y=﹣x
6.如图,在△ABC中,AB=AC,AD是边BC上的中线,若AB=5,BC=6,则AD的长为( )
A.3
B.
C.4
D.
7.设的小数部分为b,那么(4+b)b的值是( )
A.1
B.是一个有理数
C.3
D.无法确定
8.一个长方形的周长为12cm,一边长为x(cm),则它的另一条边长y关于x的函数关系用图象表示为( )
A.
B.
C.
D.
9.如图,一次函数l:y=﹣x+2的图象与x轴、y轴分别交于A、B两点,以A为直角顶点在第一象限作等腰直角三角形ABC,则直线BC的解析式是( )
A.
B.
C.
D.
10.如图,某计算机中有、、三个按键,以下是这三个按键的功能.
1.:将荧幕显示的数变成它的正平方根,例如:荧幕显示的数为49时,按下后会变成7.
2.:将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下后会变成0.04.
3.:将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下后会变成36.
若荧幕显示的数为100时,小刘第一下按,第二下按,第三下按,之后以、、的顺序轮流按,则当他按了第100下后荧幕显示的数是多少( )
A.0.01
B.0.1
C.10
D.100
11.已知点A(1,3),B(﹣2,3),则A,B两点间的距离是( )
A.4个单位长度
B.3个单位长度
C.2个单位长度
D.1个单位长度
12.如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:(1)∠DEF=∠DFE;(2)AE=AF;(3)AD平分∠EDF;(4)EF垂直平分AD.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共6小题,满分18分,每小题3分)
13.已知点P1(x1,y1),P2(x2,y2)是一次函数y=﹣5x+b图象上的两个点,若x1<x2,则y1
y2(填“>”“<”或“=”).
14.一蜡烛高20厘米,点燃后平均每小时燃掉4厘米,则蜡烛点燃后剩余的高度h(厘米)与燃烧时间t(时)之间的关系式是h=
(0≤t≤5).
15.已知点A(4,3),AB∥y轴,且AB=3,则B点的坐标为
.
16.已知|a﹣3|+(b﹣4)2+=0,则以a,b,c为三边的三角形的形状是
.
17.已知一个三角形工件尺寸(单位dm)如图所示,则高h=
dm.
18.如图为一次函数y=kx﹣b的函数图象,则k?b
0(请在括号内填写“>”、“<”或“=”)
三.解答题(共8小题)
19.把下列各数分别填入相应的集合中
0,﹣,,3.1415926,﹣,2π,﹣1,0.13030030003…,0.1,
(1)整数集合:{
…}
(2)分数集合:{
…}
(3)有理数集合:{
…}
(4)无理数集合:{
…}
20.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
21.计算:
22.在同一平面直角坐标系中,画出函数①y=x+3、②y=x﹣3、③y=﹣x+3④y=﹣x﹣3的图象,并找出每两个函数图象之间的共同特征.
23.作图:如图,请按要求在8×8的正方形网格中作图
(1)请在图1中画一个钝角△ABC,使它有一边与该边上的高线长度相等;
(2)请在图2画一个五边形ABCDE,是轴对称图形,且∠ABC=90°.
24.如图,小明爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算这块土地的面积,以便估算产量.小明测得AB=8m,AD=6m,CD=24m,BC=26m,又已知∠A=90°.求这块土地的面积.
25.甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟
米,乙在A地时距地面的高度b为
米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
26.某水果市场销售一种香蕉.甲店的香蕉价格为4元/kg;乙店的香蕉价格为5元/kg,若一次购买6kg以上,超过6kg部分的价格打7折.
(1)设购买香蕉xkg,付款金额y元,分别就两店的付款金额写出y关于x的函数解析式;
(2)到哪家店购买香蕉更省钱?请说明理由.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为P1、P2,
∴OP=OP1=OP2且∠P1OP2=2∠AOB=60°,
∴故△P1OP2是等边三角形.
故选:C.
2.解:A、4的算术平方根为2,正确;
B、﹣8的立方根为﹣2,错误;
C、1的平方根为1和﹣1,错误;
D、﹣4没有平方根,错误,
故选:A.
3.解:∵﹣2<﹣<0<3,
∴四个数中,最小的数是﹣2,
故选:C.
4.解:如图,
棋子“炮”的坐标为(3,﹣2).
故选:C.
5.解:A、不是一次函数,故此选项不合题意;
B、不是一次函数,故此选项不合题意;
C、不是一次函数,是二次函数,故此选项不合题意;
D、是一次函数,故此选项符合题意;
故选:D.
6.解:∵在△ABC中,AB=AC,AD是边BC上的中线,
∴BD=BC=3,AD⊥BC,
∵在Rt△ADB中,AB=5,
∴AD===4.
故选:C.
7.解:∵的小数部分为b,
∴b=﹣2,
把b=﹣2代入式子(4+b)b中,
原式=(4+b)b=(4+﹣2)×(﹣2)=3.
故选:C.
8.解:∵长方形的周长为12cm,一边长为x(cm),
则它的另一条边长y关于x的函数关系为:
y=6﹣x(0<x<6).
当x=0时,y=6,
当y=0时,x=6.
所以直线y=6﹣x与x轴、y轴的交点分别为(6,0)、(0,6).
所以B选项符合题意.
故选:B.
9.解:∵一次函数y=﹣x+2中,
令x=0得:y=2;令y=0,解得x=5,
∴B的坐标是(0,2),A的坐标是(5,0).
若∠BAC=90°,如图,作CE⊥x轴于点E,
∵∠BAC=90°,
∴∠OAB+∠CAE=90°,
又∵∠CAE+∠ACE=90°,
∴∠ACE=∠BAO.
在△ABO与△CAE中
,
∴△ABO≌△CAE(AAS),
∴OB=AE=2,OA=CE=5,
∴OE=OA+AE=2+5=7.
则C的坐标是(7,5).
设直线BC的解析式是y=kx+b,
根据题意得:,
解得,
∴直线BC的解析式是y=x+2.
故选:D.
10.解:根据题意得:=10,
=0.1,
0.12=0.01,
=0.1,
=10,
102=100,
100÷6=16…4,
则第100次为0.1.
故选:B.
11.解:由点A(1,3),B(﹣2,3)知,AB=|1﹣(﹣2)|=3,即A,B两点间的距离是3个单位长度.
故选:B.
12.解:∵AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC
∴△ABC是等腰三角形,AD⊥BC,BD=CD,∠BED=∠DFC=90°
∴DE=DF
∴AD垂直平分EF
∴(4)错误;
又∵AD所在直线是△ABC的对称轴,
∴(1)∠DEF=∠DFE;(2)AE=AF;(3)AD平分∠EDF.
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
13.解:∵k=﹣5<0,
∴y值随x值增大而减小.
又∵点P1(x1,y1),P2(x2,y2)是一次函数y=﹣5x+b图象上的两个点,且x1<x2,
∴y1>y2.
故答案为:>.
14.解:∵蜡烛点燃后平均每小时燃掉4厘米,
∴t小时燃掉4t厘米,
由题意知:h=20﹣4t.
15.解:∵A(4,3),AB∥y轴,
∴点B的横坐标为4,
∵AB=3,
∴点B的纵坐标为3+3=6或3﹣3=0,
∴B点的坐标为(4,0)或(4,6).故填(4,0)或(4,6).
16.解:∵|a﹣3|+(b﹣4)2+=0,
∴a﹣3=0,b﹣4=0,2c﹣10=0,
解得:a=3,b=4,c=5,
∴a2+b2=c2,
∴以a,b,c为三边的三角形是直角三角形,
故答案为:直角三角形.
17.解:
过点A作AD⊥BC于点D,则AD=h,
∵AB=AC=5dm,BC=6dm,
∴AD是BC的垂直平分线,
∴BD=BC=3dm.
在Rt△ABD中,
AD=dm,即h=4(dm).
答:h的长为4dm.
故答案为:4.
18.解:∵一次函数经过一、三象限,
∴k>0,
∵一次函数与y轴的交于正半轴,
∴﹣b>0,
∴b<0,
∴k?b,<0,
故答案为:<
三.解答题(共8小题)
19.解:=4,=﹣5,
(1)整数集合:{0,,,…};
(2)分数集合:{﹣,3.1415926,0.1,…};
(3)有理数集合:{0,﹣,,3.1415926,0.1,,…};
(4)无理数集合:{﹣,2π,﹣1,0.13030030003…,…}.
故答案为:0,,;﹣,3.1415926,0.1;0,﹣,,3.1415926,0.1,;﹣,2π,﹣1,0.13030030003….
20.解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,
理由如下:
∵AB=AC,AE=AB,AF=AC,
∴AE=AF,
在△AOE与△AOF中,
,
∴△AOE≌△AOF(SSS),
∴∠BAD=∠CAD.
21.解:
=﹣3+2+1
=
22.解:列表:
如图所示:
由图可得,①和②图象互相平行,①和③图象与y轴交点相同,①和④图象与x轴交点相同,②和③图象与x轴交点相同,②和④图象与y轴交点相同,③和④图象互相平行.
23.解:(1)
(2)
24.解:连接BD,
∵∠A=90°,
∴BD2=AD2+AB2=100
则BD2+CD2=100+576=676=262=BC2,因此∠CBD=90°,
S四边形ABCD=S△ADB+S△CBD=AD?AB+BD?CD=×6×8+×24×10=144(平方米).
25.解:(1)甲登山上升的速度是:(300﹣100)÷20=10(米/分钟),
b=15÷1×2=30.
故答案为:10;30;
(2)当0≤x<2时,y=15x;
当x≥2时,y=30+10×3(x﹣2)=30x﹣30.
当y=30x﹣30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=;
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100﹣(30x﹣30)=70时,解得:x=3;
当30x﹣30﹣(10x+100)=70时,解得:x=10;
当300﹣(10x+100)=70时,解得:x=13.
答:登山3分钟、10分钟或13分钟时,甲、乙两人距地面的高度差为70米.
26.解:(1)甲商店:y=4x
乙商店:y=.
(2)当x<6时,
此时甲商店比较省钱,
当x≥6时,
令4x=30+3.5(x﹣6),
解得:x=18,
此时甲乙商店的费用一样,
当x<18时,
此时甲商店比较省钱,
当x>18时,
此时乙商店比较省钱.
同课章节目录
